Plus Two Maths Chapter Wise Previous Questions Chapter 10 Vector Algebra

Plus Two Maths Chapter Wise Previous Questions Chapter 10 Vector Algebra are part of Plus Two Maths Chapter Wise Previous Year Questions and Answers. Here we have given Plus Two Maths Chapter Wise Previous Chapter 10 Vector Algebra.

Kerala Plus Two Maths Chapter Wise Previous Questions Chapter 10 Vector Algebra

Plus Two Maths Vector Algebra 3 Marks Important Questions

Question 1.
(i) With help of a suitable figure for any three vectorsa,bandc show that $(\bar{a}+\bar{b})+\bar{c}=\bar{a}+(\vec{b}+\bar{c})$
(ii) If $\bar{a}$ = i – j + k and $\bar{b}$ = 2i – 2j – k. What is the projection of a on b? (March – 2011)
Answer:
(i) Answered in previous years questions
No. 1(ii) (6 Mark question)
(ii) Projection of $\bar{a} \text { on } \bar{b}=\frac{\bar{a} \cdot \bar{b}}{|\bar{b}|}=\frac{2+2-1}{\sqrt{4+4+1}}=1$

Question 2.
(i) If $\bar{a}$ = 3i – j – 5k and $\bar{b}$ = i – 5j + 3k Show that $\bar{a}$ + $\bar{b}$ and a bare perpendicular.
(ii) Given the position vectors of three points as A(i – j + k); B(4i + 5j + 7k) C(3i + 3j + 5k)
(a)Find $\bar{AB}$ and $\bar{BC}$
(b) Prove that A,B and C are collinear points. (March – 2011)
Answer:

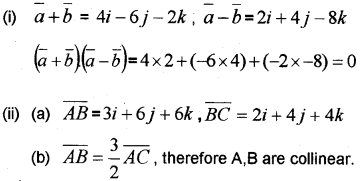
Question 3.
(i) Write the unit vector in direction of i + 2j – 3k.
(ii) If $\overline{P Q}$ = 31 + 2j — k and the coordinate of P are(1, -1,2) , find the coordinates of Q. (May – 2012)
Answer:

Question 4.
(a) The angle between the vectors $\bar{a}$ and $\bar{b}$ such that $|\vec{a}|=|\bar{b}|=\sqrt{2}$
$\bar{a}$.$\bar{b}$ = 1 is
$\begin{array}{lll} \text { (i) } \frac{\pi}{2} & \text { (ii) } \frac{\pi}{3} & \text { (iii) } \frac{\pi}{4} & \text { (iv) } 0 \end{array}$
(b) Find the unit vector along $\bar{a}-\bar{b}$ where $\bar{a}$ = i + 3j – k and $\bar{b}$ 3i + 2j + k (March -2016)
Answer:

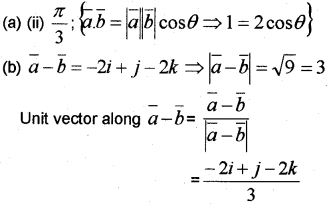
Plus Two Maths Vector Algebra 4 Marks Important Questions

Question 1.
Consider the vectors $\bar{a}$ = 21+ j – 2k and $\bar{b}$ = 6i – 3j + 2k.
(i) Find $\bar{a} \bar{b}$ and $\bar{a} \times \bar{b}$.
(ii) Verity that $|\bar{a} \times \bar{b}|=|\vec{a}|^{2}|\bar{b}|^{2}-(\bar{a} \cdot \bar{b})^{2}$ (March – 2012)
Answer:

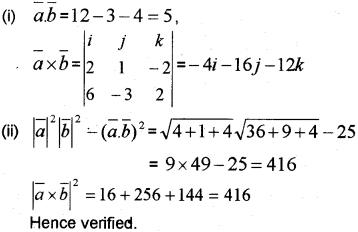
Question 2.
(i) For any three vectors $\bar{a}, \bar{b}, \bar{c}$, show that $\bar{a} \times(\bar{b}+\bar{c})+\bar{b} \times(\bar{c}+\bar{a})+\bar{c} \times(\bar{a}+\bar{b})=0$
(ii) Given A (1, 1, 1), B (1, 2, 3), C (2, 3, 1) are the vertices of MBCa triangle. Find the area of the ∆ABC (May – 2012)
Answer:

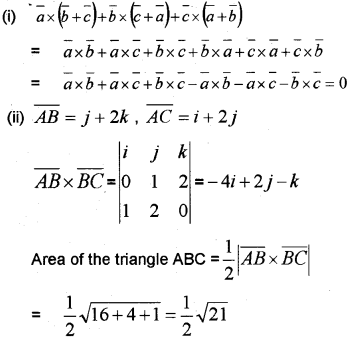
Question 3.
Consider A (2, 3, 4) , B (4, 3, 2) and C (5, 2, -1) be any three points
(i) Find the projection of $\overline{B C}$ on $\overline{A B}$
(ii) Find the area of triangle ABC (March – 2013)
Answer:

Question 4.
(i) Find the angle between the vectors $\bar{a}$ =3i + 4j + k and $\bar{b}$ = 2i + 3j – k
(ii) The adjacent sides of a parallelogram are $\bar{a}$ = 3i + λj + 4k and $\bar{b}$ = i – λj + k
(a) Find $\bar{a} \times \bar{b}$
(b) If the area of the parallelogram is square units, find the value of A (May – 2013)
Answer:

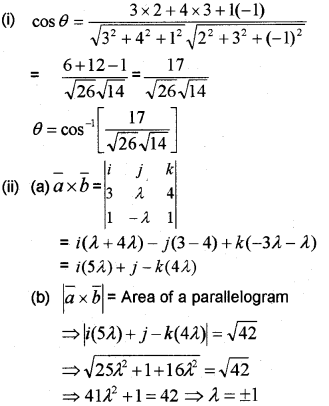
Question 5.
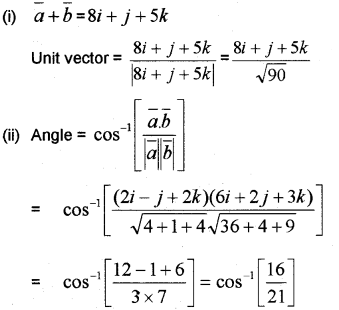
Let $\bar{a}$ = 2i – j + 2k and $\bar{b}$ = 6i + 2j + 3k
(i) Find a unit vector in the direction of $\bar{a}$ + $\bar{b}$
(ii) Find the angle between a and b (March – 2014)
Answer:

Question 6.
Consider the triangle ABC with vertices A(1, 1, 1) , B (1, 2, 3) and C (2, 3, 1)
(i) Find $\overline{A B}$ and $\overline{A C}$
(ii) Find $\overline{A B}$ x $\overline{A C}$
(iii) Hence find the area of the triangle (March – 2014)
Answer:

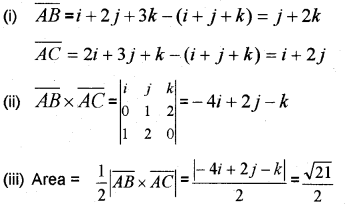
Question 7.
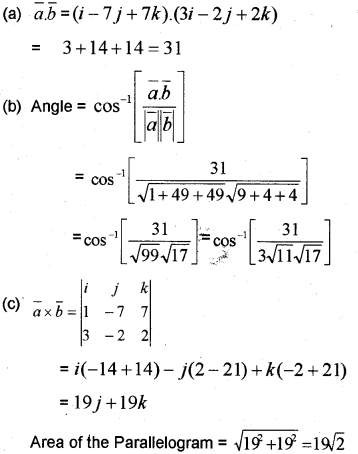
Consider the vectors $\bar{a}$ = i – 7j + 7k; $\bar{b}$ = 3i – 2j + 2k
(a) Find $\bar{a b}$.
(b) Find the angle between $\bar{a}$ and $\bar{b}$.
(c) Find the area of parallelogram with adjacent sides $\bar{a}$ and $\bar{b}$. (May – 2014)
Answer:

Question 8.
(a) If the points A and B are (1, 2, -1) and (2, 1, -1) respectively, then is
(i) i + J
(ii) i – J
(iii) 2i + j – k
(iv) i + j + k
(b) Find the value of for which the vectors 2i – 4j + 5k, i – λj + k and 3i + 2j – 5k are coplanar.
(c) Find the angle between the vectors a = 2i + j – k and b = i – j + k (March – 2016)
Answer:

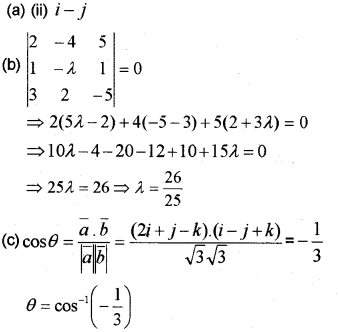
Question 9.
(i) $(\bar{a}-\bar{b}) \times(\bar{a}+\bar{b})$ is equaito
$\begin{array}{lll} \text { (a) } \bar{a} & \text { (b) }|\bar{a}|^{2}-|\bar{b}|^{2} & \text { (c) } \bar{a} \times \bar{b} \text { (d) } 2(\bar{a} \times \bar{b}) \end{array}$

(ii) If $\bar{a}$ and $\bar{b}$ are any two vectors, then
$(\bar{a} \times \bar{b})^{2}=\left|\begin{array}{ll} \bar{a} \cdot \bar{a} & \bar{a} \cdot \bar{b} \\ \bar{a} \cdot \bar{b} & \bar{b} \bar{b} \end{array}\right|$

(iii) Using vectors, show that the points A(1, 2, 7), B(2, 6, 3), C(3, 10, -i) are collinear. (May – 2016)
Answer:

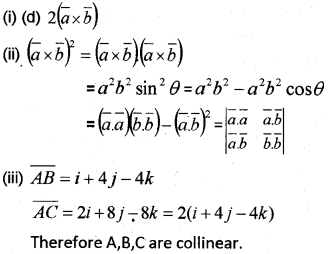
Plus Two Maths Vector Algebra 6 Marks Important Questions

Question 1.
(i) Find a vector in the direction of $\bar{r}$ = 3E – 4j that has a magnitude of 9.
(ii) For any three vectors $\bar{a,b}$ and $\bar{c}$, and Prove that $(\bar{a}+\bar{b})+\bar{c}=\bar{a}+(\bar{b}+\bar{c})$.
(iii) Find a unit vector perpendicular to $\bar{a}+\bar{b}$ and $\bar{a}-\bar{b}$, where $\bar{a}$ = i – 3j + 3k and $\bar{b}$ and $/bar{c}$ = 3E—3j+2k. (March – 2010)
Answer:
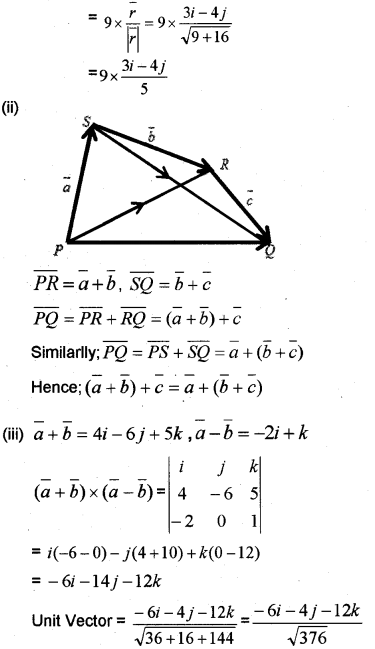
(i) Unit vector of magnitude 9

Question 2.
Let A(2, 3, 4), B(4, 3, 2) and C(5, 2, -1) be three points
(i) Find $\overline{A B}$ and $\overline{B C}$
(ii) Find the projection of $\overline{B C}$ on $\overline{A B}$
(iii) Fiñd the area of the triangle ABC. (May – 2010)
Answer:

Question 3.
ABCD s a parallelogram with A as the origin, $\bar{b}$ and $\bar{d}$ are the position vectors of B and D respectively.

(i) What is the position vector of C?
(ii) What is the angle between $\bar{AB}$ and $\bar{AD}$?
(iii) If $|\overrightarrow{A C}|=|\overrightarrow{B D}|$, show that ABCD is a rectangle. (May – 2011)
Answer:
(i) Since ABCD is a parallelogram with A as the

Question 4.
(a) If $\bar{a}, \bar{b}, \bar{c}, \bar{d}$ respectively are the position vectors representing the vertices A,B,C,D of a parallelogram, then write $/bar{d}$ in terms of $\bar{a}, \bar{b}, \bar{c}$.
(b) Find the projection vector of $/bar{b}$ = i + 2j + k along the vector $/bar{a}$ = 21 – i – j + 2k. Also write $/bar{b}$ as the sum of a vector along $/bar{a}$ and a perpendicular to $/bar{a}$.
(C) Find the area of a parallelogram for which the vectors 21 + j, 31 + j +4k are adjacent sides. (March – 2015)
Answer:

Question 5.
(a) Write the magnitude of a vector $/bar{a}$ in terms of dot product.
(b) If $\bar{a}, \bar{b}, \bar{a}+\bar{b}$ are unit vectors, then prove that the angle between $/bar{a}$ and $/bar{b}$ is $\frac{2 \pi}{3}$
(c) If 2i + j – 3k and mi + 3j – k are perpendicular to each other, then find ‘m’.
Also find the area of the rectangle having these two vectors as sides. (March – 2015)
Answer:

Question 6.
Consider the triangle ABC with vertices A(1, 2, 3), B(-1, 0, 4), C(0, 1, 2)
(a) Find $\overline{A B}$ and $\overline{A C}$
(b) Find $\angle A$
(c) Find the area of triangle ABC. (May – 2015)
Answer:

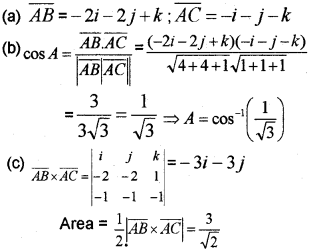
We hope the Plus Two Maths Chapter Wise Previous Questions Chapter 10 Vector Algebra help you. If you have any query regarding Kerala Plus Two Maths Chapter Wise Previous Questions Chapter 10 Vector Algebra, drop a comment below and we will get back to you at the earliest.