Plus Two Chemistry Notes Chapter 2 Solutions is part of Plus Two Chemistry Notes. Here we have given Plus Two Chemistry Notes Chapter 2 Solutions.
| Board | SCERT, Kerala |
| Text Book | NCERT Based |
| Class | Plus Two |
| Subject | Chemistry Notes |
| Chapter | Chapter 2 |
| Chapter Name | Solutions |
| Category | Plus Two Kerala |
Kerala Plus Two Chemistry Notes Chapter 2 Solutions
Solutions:
homogeneous mixtures of two or more pure substances, having uniform composition and properties throughout. The substances forming a solution are called components.
Solvent and Solute:
The component that is present in the largest quantity is known as solvent.
One or more components present in the solution other than solvent are called solutes. e.g. In sugar solution, water is the solvent and sugar is the solute.
Binary solution:
A solution containing only two components.
Aqueous solutions:
solutions in which the solvent is water.
Types of Solutions
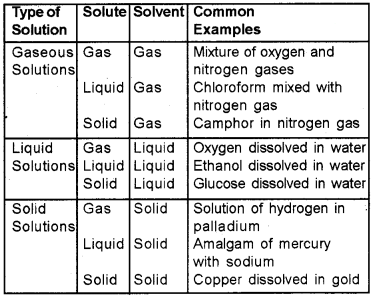
Expressing Concentration of Solutions :
The concentration of a solution is defined as the amount of solute present in the given quantity of the solution.
1. Mass percentage (w/w) :
The mass % of a component in a given solution is the mass of the component (solute) per 100 g of solution.
![]()
e.g. 10% glucose solution means 10 g of glucose dissolved in 90 g of water resulting in a 100 g solution.
2. Volume percentage (v/v) :
The volume % of a component in a given solution is the volume of the component per 100 volume of solution.
![]()
Example:
10% ethanol solution means 10 mL of ethanol dissolved in 90 mL of water.
3. Mass by volume percentage (w/v):
It is the mass of solute dissolved in 100 mL of the solution. Used in medicine and pharmacy.
4. Parts per million (ppm):
It is the parts of a solute (component) per million parts of the solution. When a solute is present in very minute amounts, parts per million (ppm) is used.

5. Mole fraction (X):
ratio of number of moles of one component to the total number of moles of all the components present in the solution.
![]()
For a binary solution, nA be the number of moles of A and nB be the number of moles of B.
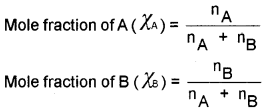
The sum of mole fractions of all the components present in the solution is always equal to 1.
i.e., χA + χB = 1
Fora solution containing ‘i’ number of components,
χ1 + χ2 +……………… + χi = 1
Mole fraction is independent of temperature.
6. Molarity (M):
number of moles of solute dissolved in one litre of the solution.
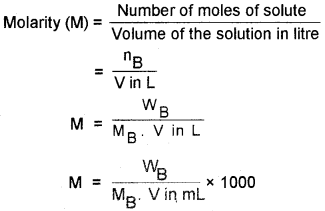
7. Molality (m):
number of moles of solute per kilogram of the solvent.
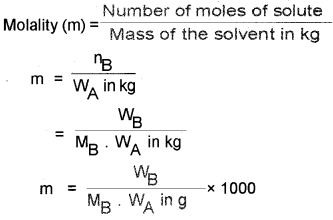
Solubility:
Solubility of a substance is its maximum amount that can be dissolved in a specified amount of solvent at a particular temperature.
Factors affecting solubility
Nature of the solute, nature of the solvent, temperature ‘ and pressure
Solubility of Solids in Liquids :
Like dissolves like:
Polar solutes are soluble in polar solvents and non-polar solutes are soluble in non-polar solvents.
Unsaturated solution:
Solution in which more solute can be dissolved at the same temperature.
Saturated solution:
Solution in which no more solute can be dissolved at the same temperature and pressure.
Effect of temperature :
Solubility increases with temperature if the reaction is endothermic. Solubility decreases with temperature if the reation is exothermic.
Effect of pressure :
Pressure does not have any significant effect on solubility of solids in liquids because solids and liquids are highly incompressible and practically remain unaffected by changes in pressure.
Solubility of a Gas in a Liquid :
It is greately affected by pressure and temperature.
Effect of pressure
Henry’s law :
The law states that at a constant temperature, the solubility of a gas in a liquid is directly proportional to the pressure of the gas.
The most commonly used form of Henry’s law states that the partial pressure of the gas in the vapour phase (p) is proportional to the molefraction of the gas (χ) in the solution.
P = KH.χ
where KH is the Henry’s law constant.
Different gases have different KH values at the same temperature. Thus, KH is a function of the nature of the gas.
Higher the value of KH at a given pressure, the lower is the solubility of the gas in the liquid.
The solubility of gases increase with decrease of temperature. Therefore, aquatic species are more comfortable in cold waters rather than in hot waters.
Applications of Henry’s law
1. To increase the solubility of CO2 in soft drinks and soda water, the bottle is sealed under high pressure.
2. To avoid bends (a medical condition which is painful and dangerous to life caused by the formation of bubbles of N2 in the blood) the tanks used by scuba divers are filled with air diluted with He (11.7% He, 56.2% N2 and 32.1% O2).
3. At high altitudes, low pressure leads to low concentrations of O2 in blood. It causes climbers to become weak and unable to think clearly (anoxia).
Effect of temperature :
Dissoloution of gases in liquids is an exothermic process. Hence, according to Le Chatelier’s principle solubility of gases in liquids decreases with rise in temperature.
Vapour Pressure of Liquid Solutions
Vapour Pressure of Liquid-Liquid Solutions:
Consider the two volatile liquids denoted as ‘A’ and ‘B’. When both liquids are taken in a closed vessel, both components would evaporate and an equilibrium would be established between liquid and vapour phase.
Let, PA– Partial vapour pressure of component A’
PB – Partial vapour pressure of component ‘B’
χA Mole fraction of A
χB Moiefraction of B
Raoult’s Law :
The law states that fora solution of volatile liquids, the partial vapour pressure of each component in the solution is directly proportional to its mole fraction.
For component ‘A’
PA ∝ χA.
PA= P°A χA
where P°A is the vapour pressure of pure component ‘A’ at the same temperature.
Similarly, for component ‘B’
PB ∝ χB
PB= P°B χB
where PB° is the vapour pressure of pure component ‘B’. Rauolt’s law also states that, at a given temperature for a solution of volatile liquids, the partial vapour pressure of each component is equal to the product of the vapour pressure of pure component and its mole fraction.
According to Dalton’s law of partial pressures,
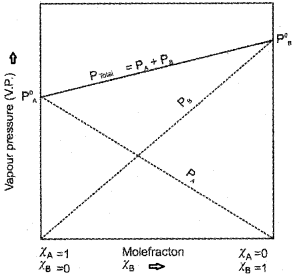
Total pressure, P[Total] = PA + PB
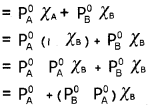
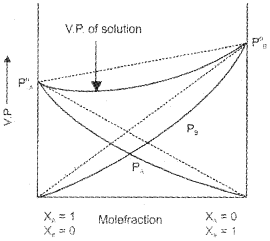
A plot of PA or PB versus the mole fractions χA and χB for a solution gives a linear plot as shown in the figure.
Raoult’s Law as a special case of Henry’s Law:
According to Raoult’s law, the vapour pressure of volatile liquid in a solution is proportional to its mole fraction, i.e., Pi = Pi° χi
According to Henry’s law, the vapour pressure of a gas in a liquid is proportional to its mole fraction, i. e., p=KHχ
Thus, Raoult’s law becomes a special case of Henry ’s law in which KH becomes equal to Pi°.
Vapour Pressure of Solution of Solids in Liquids:
If a non-volatile solute is added to a solvent to give a solution, the surface of solution has both solute and solvent molecules; thereby the fraction of surface covered by the solvent molecules gets reduced. Consequently, the number of solvent molecules escaping from the surface is reduced. Hence, the vapour pressure of solution is lower than vapour pressure of pure solvent.
General form of Raoult’s Law:
For any solution, the partial vapour pressure of each volatile component in the solution is directly proportional to its mole fraction.
In a binary solution, let us denote the solvent by ‘A’ and solute by ‘B’.
According to Raoult’s law,
PA ∝ χA
PA = PA° χA
Total pressure, P = PA Here, PB = 0
(∵ solute is non-volatile)
P = PA° χA
For binary solution,
χA + χB = 1
χA = 1 – χB
Thus, the above equation becomes,

lowering of vapour pressure.
Ideal and Non-ideal Solutions :
Ideal Solutions:
The solutions which obey Raoult’s law over the entire range of concentrations.
Important properties of Ideal Solutions
i. PA = P°A χA ; PB = P°B χB
ii. Enthalpy of mixing is zero (∆mixH = 0)
iii. Volume of mixing is zero (∆mixV = 0)
If the intermolecular attractive forces between A – A and B – Bare nearly equal to those between A – B, it leads to the formation of ideal solution.
Examples:
- Solution of n-hexane and n-heptane
- Solution of bromoethane and chloroethane
- Solution of benzene and toluene
Non-ideal Solutions :
solutions which do not obey Raoult’s law overthe entire range of concentration. The vapour pressure of such solutions is either higher or lower than that predicted by Raoult’s law.
If the vapour pressure is higher, it exhibits positive deviation and if the vapour pressure is lower it exhibits negative deviation from the Raoult’s law.
Solutions showing positive deviation :
the intermolecular attractive forces between the solute- solvent molecules are weaker than those between the solute-solute and solvent-solvent molecules. Thus, in such solutions molecules will find it easier to escape than in pure state. This will increase the vapour pressure and results in the positive deviation.
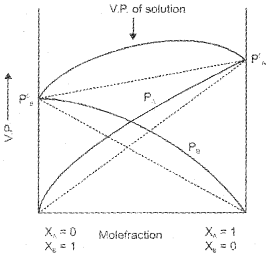
(dotted line represents graph for ideal solution).
Examples:
Ethanol + Water, Ethanol + Acetone, CCl4 + Chloroform, C6H6 + Acetone , n-Hexane + Ethanol
Solution showing negative deviation:
In the case of negative deviation, the intermolecular attractive forces between solvent-solute molecules are greater than those between solvent-solvent and solute-solute molecules and leads to decrease in the vapour pressure.
Examples:
1. Mixture of phenol and aniline – In this case the intermolecular hydrogen bonding between phenolic proton and lone pair on nitrogen atom of aniline is stronger than the respective intermolecular hydrogen bonding between similar molecules.
2. Mixture of acetone and chloroform – Here chloroform molecule is able to form hydrogen bond with acetone molecule.
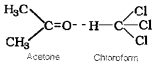
3. H2O + HCl, (4) H2O + HNO3, (5) CHCl3 + (C2H5)2O
Azeotropes:
binary mixtures having same composition in liquid and vapour phase and boil at a constant temperature. It is not possible to separate the components of azeotropes by fractional distillation.
Solutions which show large positve deviation from Raoult’s law form minimum boiling azeotrope at a specific composition. For example, ethanol-water mixture forms a minimum boiling azeotrope (b.p. 351.1 K) when approximately 95% by volume of ethanol is reached.
The solutions that show large negative deviation from Raoult’s law form maximum boiling azeotrope at a specific composition. For example, nitric acid and water form a maximum boiling azeotrope (b.p. 393.5 K) at the approximate composition, 68% nitric acid and 32% water by mass.
Colligative Properties :
properties which depend on the number of solute particles irrespective of their nature relative to the total number of particles present in the solution. These are,
i. Relative lowering of vapour pressure of the solvent (Δp1p01)
ii. Elevation of boiling point of the solvent (∆Tb)
iii. Depression of freezing point of the solvent (∆Tf)
iv. Osmotic pressure of the solution (π)
Relative Lowering of Vapour Pressure:
When a non-volatile solute (B) is dissolved in a liquid solvent (A), the vapour pressure of the solvent is lowered. This phenomenon is called lowering of vapour pressure. It depends only on the concentration of the solute particles and it is independent of their identity. The relation between vapour pressure of solution, mole fraction and vapour pressure of the solvent is given as,
PA = χAP°A ……………(1)
The lowering of vapour pressure of solvent ∆ PA is given as,
∆ PA = P°A – PA ……………(2)
Substitute the equation (1) in (2)
∆ PA = P°A – P°AχA
= P°A(1 – χA)
∆ PA = P°AχB …………..(3) ∵ (1 – χA) = χB
The relative lowering of vapour pressure is given as,

of vapour pressure and is equal to the mole fraction of solute.
From equation (4),
![]()
For dilute solutions nB < < nA, hence neglecting nB In the denominator, the above equation becomes,
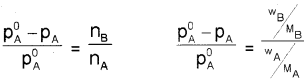
where wA and wB are the masses and MA and MB are the molar masses of solvent and solute respectively.
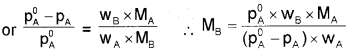
Elevation of boiling point (∆Tb):
The boiling point of a solution is higher than that of the pure solvent. The elevation in the boiling point depends ‘ on the number of solute molecules rather than on their nature.
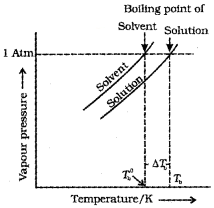
Let T°b be the boiling point of pure solvent and Tb be the boiling point of solution. The increase in the boiling point ∆Tb = Tb – T°b is known as elevation of boiling point.
For a dilute solution, the elevation of boiling point ( ∆Tb) is directly proportional to the molal concentration of the solute in a solution (i.e., molality).
∆Tb ∝ m
∆Tb = Kbm …………(1)
where, m → molality and Kb → Boiling Point Elevation Constant/Molal Elevation Constant/ Ebullioscopic Constant.
Unit of Kb is K kg mol-1 Or K m-1
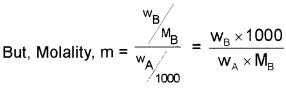
Substituting the value of‘m’ in equation (1),
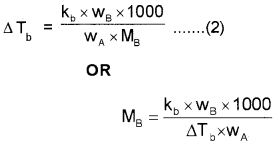
Depression of Freezing point (∆Tf) :
The lowering of vapour pressure of a solution causes a lowering of the freezing point compared to that of the pure solvent.
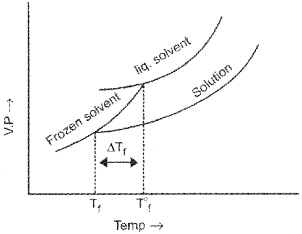
Let T°f be the freezing point of pure solvent and Tf be the freezing point of solution.
Depression in freezing point ∆Tf= T°f – Tf
For a dilute solution, depression of freezing point (∆Tf) is directly proportioned to molality (m) of the solution. Thus,
∆Tf ∝ m
∆Tf = Kfm ………………(1)
where, Kf – Freezing Point Depression Constant/ Molal Depression Constant/Cryoscopic Constant.
Unit of Kf is K kg mol-1 Or K m-1
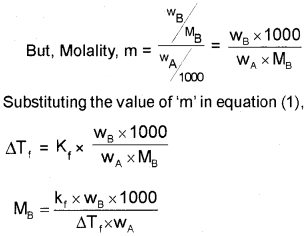
[Note: The values of Kb and Kf, depend upon the nature of the solvent. They Can be ascertained from the following equations:
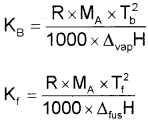
where,
R → Gas constant, MA → Molar mass of solvent
Tb → Boiling point of pure solvent of kelvin
Tf → Freezing point of pure solvent in kelvin
∆fusH → Enthalpy of fusion, ∆vapH → enthalpy of vapourisation.
For water, Kb = 0.52 K kg mol-1 and Kf = 1.86 K kg mol-1]
Osmosis and Osmotic Pressure:
The process of flow of the solvent molecules from pure solvent to the solution through semipermeable membrane (SPM) is called osmosis.
Semi Permeable Membrane :
The membrane which allows the passage of solvent molecules but ’ not the solute molecule is called SPM.
Example:
Parchment paper, Pig’s bladder, Cell wall, Film of cupric ferrocyanide.
Osmotic Pressure (π):
the excess pressure which must be applied to a solution to prevent osmosis or the pressure that just stops the flow of solvent.
Osmotic pressure (π) is proportional to the molarity (C) of the solution at a given temperature (T K).
π = CRT, where R is the gas constant.
π = nBVRT, where nc is the number of moles of the solute and V is the volume of the solution in litres.
π = nBRT
π V= WBMBRT , where wB is the mass of the solute and MB is the molar mass of the solute.
Or MB = wBRTπV
Osmotic pressure measurement is widely used to determine molar mass of proteins, polymers and other macro molecules.
Advantages of osmotic pressure method:
i) pressure measurement is around the room temperature
ii) molarity of the solution is used instead of molality
iii) the magnitude of osmotic pressure is large compared to other colligative properties even for very dilute solutions.
Isotonic Solution :
Two solutions having same (equal) osmotic pressure at a given temperature. A 0.9% solution of NaCI (normal saline solution) is isotonic with human blood, and it is safe to inject intravenously.
Hypertonic Solution :
A solution having higher osmotic pressure than another solution.
Hypotonic Solution :
A solution having lower osmotic pressure than another solution.
Reverse Osmosis:
flow of the pure solvent from solution side to solvent side through semipermeable membrane when a pressure larger than the osmotic pressure is applied to the solution side.
Uses of reverse osmosis:
Desalination of sea water, Purification of water.
Abnormal Molar Mass :
In some cases, the molar mass determined by colligative properties do not agree with the theoretical values. This is due to association ordissociation of the solute particles in the solution.
Association of Solute Particles :
When solute particles undergo association the number of the solute particles in the solution decreases. Consequently, the experimental values of colligative properties are less than the expected values, e.g. Molecules of ethanoic acid (acetic acid) dimerise in benzene due to intermolecular hydrogen bonding.
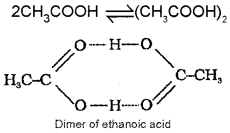
Similarly, benzoic acid undergo dimerisation when dissolved in benzene.
Dissociation of Solute Particles :
When the solute particles dissociate or ionise in the solvent, the number of particles in solution increases and so the experimental values of the colligative properties are higher than the calculated values.
e.g. KCl in water ionises as
KCl → K+ + C–
Molar mass either lower or higher than the expected or normal value is called as abnormal molar mass.
van’t Hoff factor (i):
It accounts for the extent of association or dissociation.

Significance of van’t Hoff factor.
i > 1 ⇒ there is dissociation of solute particles.
i < 1 ⇒ there is association of solute particles.
i < 1 ⇒ there is no dissociation and association of solute particles.
Inclusion of van’t Hoff factor modifies the equations for colligative properties as follows:
Relative lowering of vapour pressure of solvent,

We hope the Plus Two Chemistry Notes Chapter 2 Solutions help you. If you have any query regarding Plus Two Chemistry Notes Chapter 2 Solutions, drop a comment below and we will get back to you at the earliest.
