Kerala Plus One Physics Notes Chapter 14 Oscillations
Introduction
In this chapter, we study oscillatory motion. The description of an oscillatory motion requires some fundamental concept like period, frequency, displacement, amplitude and phase.
Periodic And Oscillatory Motions
Periodic Motion:
A motion that repeats itself at regular intervals of time is called periodic motion.
Example:
- The orbital motion of planets in the solar system.
- The piston in a steam engine going back and forth
Oscillations or Vibrations:
A body executes to and fro motion at regular intervals of time is called oscillatory (or) vibratory motion.
Note:
(1) When the frequency is small, we call it oscillation. When the frequency is high, we call it vibration.
Period and frequency:
Period (T):
Time taken to complete one oscillation is called period
Frequency (n):
The number of oscillations per second is called frequency.
frequency v = \(\frac{1}{T}\)Hz
Displacement:
Displacement of oscillation means the change of any physical property with time under consideration.
Explanation:
For example, consider the oscillation of block attached to a spring. In this case the displacement of block with time is referred to as displacement.
In the case if oscillation of simple pendulum, the angle from the vertical as a function of time may be regarded as a displacement variable. The voltage across a capacitor, changing with time in an a.c. circuit is also a displacement variable
Note:
The displacement variable may take both positive and negative values.
Mathematical expression for displacement:
The displacement of a periodic function can be written as

Simple Harmonic Motion (S.H.M.)
Simple harmonic motion is the simplest form of oscillatory motion.
The oscillatory motion is said to be simple harmonic motion if the displacement ‘x’ of the particle from the origin varies with time as
![]()
Where
x(t) = displacement x as a function of time t
A = amplitude
ω = angular frequency
(ω t+ Φ) = phase (time-dependent)
Φ = phase constant or initial phase
Graphical Variation of S.H.M.
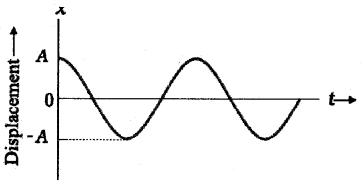
The above graph shows the graphical representation of x(t) = A cos wt with time.
(Initial phase Φ = 0)
Amplitude of S.H.M.
The maximum displacement of S.H.M. from mean position is called the amplitude of S.H.M.
Note:
1.
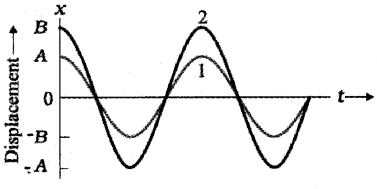
Two simple harmonic motions having, same w and Φ but different amplitudes A and B as shown in the above figure.
2.
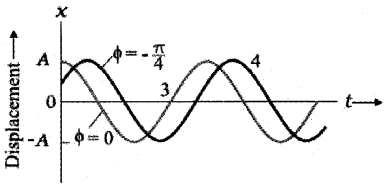
Two simple harmonic motions having the same A and w but different phase angle Φ as shown in the above figure.
Simple Harmonic Motion And Uniform Circular Motion
Question 1.
Show that the projection of uniform circular motion on any diameter of the circle is S.H.M.
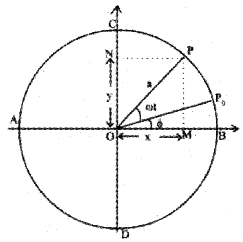
Answer:
Consider a particle moving along the circumference of a circle of radius ‘a’ and centre O, with uniform angular velocity w. AB and CD are two mutually perpendicular diameters along X and Y axis. At time t = 0. let the particle be at P0 so that ∠P0OB = Φ.
After time Y second, let the particle reach P so that ∠POP0 = ωt. N is the foot of the perpendicular drawn from P on the diameter CD.
Similarly, M is the foot of the perpendicular drawn from P to the diameter AB. When the particle moves along the circumference of the circle, the foot of the perpendicular executes to and fro motion along the diameter CD or AB with O as the mean position. From the right angle triangle O MP, we get
cos (ωt + Φ) = \(\frac{\mathrm{OM}}{\mathrm{OP}}\)
∴ OM = OP cos (ωt + Φ)
X = a cos (ωt + Φ) ………………. (1)
Similarly, we get
sin (ωt + Φ) = \(\frac{y}{a}\) (or)
Y = a sin (ωt + Φ) ……………… (2)
Equation (1) and (2) are similar to equations of S.H.M. The equation(1) and (2) shows that the projection of uniform circular motion on any diameter is S.H.M.
At t = 0, if the particle is at B, then Φ = 0. Then equations (1) and (2) reduce to
x = a cos ωt ………………….. (3)
y = a sin ωt …………………….(4)
Velocity And Acceleration In Simple Harmonic Motion B
Velocity Of S.H.M.
The y displacement of S.H.M. is given by
y = a sin ω t
∴ velocity in y-direction
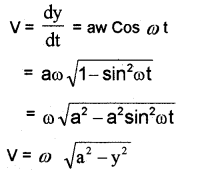
Case – 1
At the mean position y=0, therefore velocity is maximum. The maximum velocity is given by
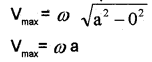
Case – 2
At the extreme position, y = a
∴ Vminimum = \(\sqrt{a^{2}-a^{2}}\) = 0
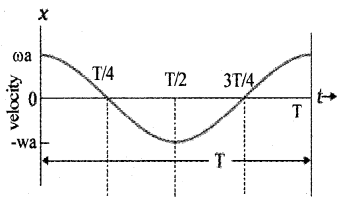
So the velocity of a S.H.M. varies between o and wa
Acceleration of S.H.M
We know y = a sin ω t
Velocity v = \(\frac{d y}{d t}\) = a ω cos ω t
Acceleration a = \(\frac{d^{2} y}{d t^{2}}\) = -aω² sin ωt
a = -aω² sin ωt
![]()
This equation shows that the acceleration of an SHM is directly proportional to the displacement and opposite to the displacement.
Variation of displacement Y with time t:
Variation of velocity (v) with time:
Variation of acceleration with time:
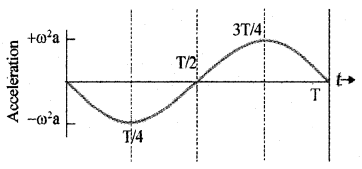
Force Law For Simple Harmonic Motion
According to Newton’s second law of motion F = ma
But a = -ω²y(t)
ie. force acting on the S.H.M. in Y direction
F = -mω²y(t)
(or) F = -ky(t)
Where k= mω²
From the above equation (1), we can take an alternative definition of simple harmonic motion.
Statement:
Simple harmonic motion is the motion executed by a particle subject to a force, which is proportional to the displacement of the particle and is directed towards the mean position.
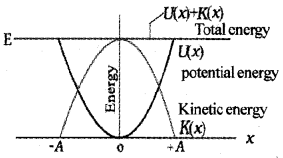
Energy In Simple Harmonic Motion
A simple harmonically moving particle possesses both potential energy and kinetic energy. Potential energy is due to its displacement against restoring force. Kinetic energy is due to its motion.
Total energy of the S.H.M. is the sum of the kinetic energy and potential energy. Total energy remains a constant throughout its motion.
Expression for Kinetic energy:
Let m be the mass of the particle executing SHM. Let V be the velocity at any instant,
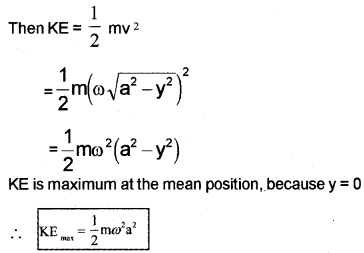
Expression for potential energy:
Potential energy is work required to take the particle against the restoring force.
Work done to displace the particle through a small distance dy, dw = force × displacement
= mω²y × dy [force = ω²y ]. Therefore total work done to take the particle from o to y.
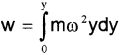
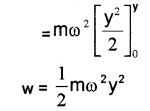
This work done is stored in the particle as its potential energy.
![]()
At extreme position y = a
![]()
At equilibrium position y = 0
∴ PE = 0
Total energy of an S.H.M.
Total energy = PE + kE
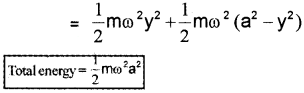
∴ Total energy = maximum KE = maximum PE
Graphical variation of PE, KE and TE of S.H.M.
Some Systems Executing Simple Harmonic Motion
Oscillations due to a spring Hooks Law:
The force acting simple harmonic motion is proportional to the displacement and is always directed towards the centre of motion.
F α – x (or) F= kx
where k is called spring constant
Period of oscillation of a spring:
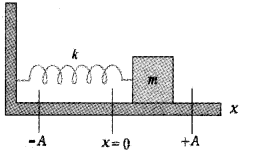
Consider a body of mass m attached to a massless spring of spring constant K. The other end of spring is connected to a rigid support as shown in figure. The body is placed on a frictionless horizontal surface.
If the body be displaced towards right through a small distance ‘x’, a restoring force will be developed.

The Simple Pendulum:
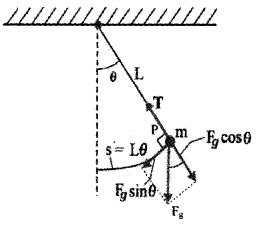
Consider a mass m suspended from one end of a string of length L fixed at the other end as shown in figure. Suppose P is the instantaneous position of the pendulum. At this instant its string makes an angle θ with the vertical.
The forces acting on the bob are (1) weight of bob Fg (mg) acting vertically downward. (2) Tension T in the string.
The gravitational force Fg can be divided into a radial component FgCos θ and tangential component FgSin θ. The radial component is cancelled by the – tension T. But the tangential component FgSin θ produces a restoring torque.
Restoring torque τ = – Fg sin θ . L.
τ = -mg sin θ.L …………….. (1)
-ve sign shown that the torque and angular displacement θ are oppositely directed. For rotational motion of bob,.
τ = Iα …………. (2).
Where I is a moment of inertia about the point of suspension and α is angular acceleration. From eq (1) and eq (2).
Iα = -mg sin θ.L
If we assume that the displacement θ is small, sin θ ≈ θ.
∴ Iα = -mg θ.L
Iα + mg θ.L = 0

Damped Simple Harmonic Motion
Periodic oscillations of decreasing amplitude due to the presence of resistive forces of the medium are called damped oscillations.
Question 2.
Derive a differential equation for a damped simple harmonic oscillation.
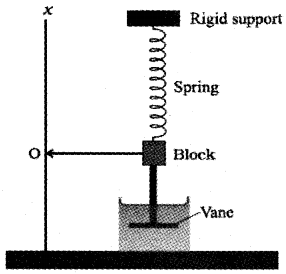
Answer:
Consider a block of mass ‘m’ connected to one end of a massless spring of spring constant K. The other end of spring is connected to rigid support. The block is connected to a vane through a rod (The vane and rod are massless). The vane is submerged in a liquid.
Let the equilibrium position of block be ‘O’. If this block is moved along downward direction through a distance x, a damping force will be developed on vane due to liquid. This damping force is proportional to velocity of vane ie; damping force Fd α – v (or) Fd = -bv
where b is called damping constant. The value of b depends on the characteristics of the liquid and the vane.
The restoring force on the block due to spring. Fs = -kx. where x is the displacement of the mass from its equilibrium position.
∴ Total force on the block, F = -bv + -kx
ma = -bv + -kx
ma + bv + kx = 0
\(m \frac{d^{2} x}{d t^{2}}+b \frac{d x}{d t}+k x=0\)
This is the differential equation of S.H.M.
The motion of damped harmonic oscillator:
The solution of the above differential equation of damped harmonic oscillator is
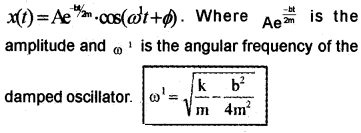
Case – 1
b = 0 (There is no damping force). In this case, we get
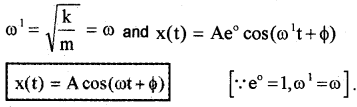
The above result shows that, if there is no damping force (b = 0). The oscillator behaves like a undamped oscillator.
Case – 2
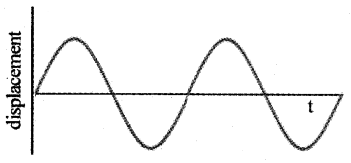
If b is small, the amplitude of the oscillator decreases continuously with time. The motion is approximately a periodic. The Variation of displacement x (t) with time T is shown below.

Case – 3
If damping constant b is large, the amplitude of the oscillator decreases to zero very quickly. The motion is not a periodic motion. The variation of displacement x (t) with time T is shown below.

The Energy variation of damped oscillator:
The energy of an undamped oscillator, E = \(\frac{1}{2}\)kA².
where A is the amplitude of an undamped oscillator. But for the damped oscillator, amplitude = Ae-bt/2m.
![]()
The above equation shows that the energy of a damped oscillator decreases exponentially with time, which is shown below
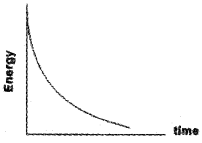
Note:
Small damping means that the dimensionless ratio
\((b / \sqrt{k m})\) is much less than 1.
Forced oscillations and resonance
Free oscillation:
When a body oscillates in the absence of external forces (eg. friction etc.) the oscillations are said to be free oscillations.
Forced oscillation:
When an external periodic force is applied to a damped harmonic oscillator, the oscillator will vibrate with a constant amplitude and frequency of vibration will be that of the applied periodic force. This type of oscillation is called forced oscillation.
The differential equation of forced oscillator:
Let F(t) = F0 cosωdt is an external force applied to a damped oscillator.
The total force acting on the damped oscillator,
F = – bv – kx + F0 cosωdt
where -bv is the damping force and -kx is the linear restoring force.
F + bv + kx = F0 cosωdt
\(m \frac{d^{2} x}{d t^{2}}+b \frac{d x}{d t}+k x=F_{0} \cos \omega_{d} t\)
This is the differential equation of an oscillator of mass m on which a periodic force of (angular) frequency ωd is applied. The oscillator initially oscillates with its natural frequency w. When we apply the external periodic force, the oscillation with the natural frequency die out, and the body oscillates with the (angular) frequency of the external periodic force.
The motion of forced oscillator:
The solution (displacement) of the above differential equation of forced oscillator can be written as
x(t) = Acos(ωdt + Φ)
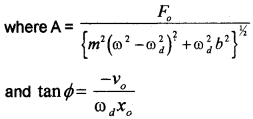
where m is the mass of the particle v0 and x0 are the velocity and the displacement of the particle at time t = 0, (which is the moment when we apply the periodic force)
Case -1
When b = 0 (damping force = 0) and ω = ωd,
we get A = \(\frac{F_{0}}{0}\)
A = ∞
This is an ideal case. This case never arises in a real situation as the damping is never perfectly zero.
Case – 2
(Small damping, driving frequency far from natural frequency).
In this ωdb << m(ω² – ωd²). Hence we can neglect ωdb. Hence amplitude of oscillation can be written as.
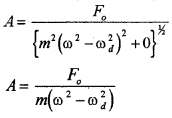
Case – 3
(Small damping, driving frequency close to natural frequency).
In this case m(ω² – ωa²) << ωdb. Hence we can neglect m (ω² – ωa²). Hence amplitude of oscillation can be written as
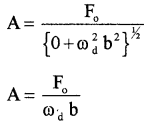
This equation shows that the maximum amplitude fora given driving frequency is governed by the driving frequency and damping constant.
Resonant Oscillation
When the frequency of the external periodic force is varied, it is found that the amplitude of the forced vibration increases and reaches a maximum value and then decreases.
The amplitude will be maximum when the frequency of the applied periodic force is equal to the natural frequency of the vibration. Such oscillations are called resonant oscillations and the phenomenon is called resonance.
Graphical variation amplitude with driving frequency:
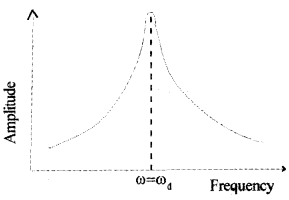
Examples of resonance:
All mechanical structures have one or more natural frequencies, and if a structure is subjected to a strong external periodic driving force that matches one of these frequencies, the resulting oscillations of the structure may rupture it.
The Tacoma Narrows Bridge at Puget Sound, Washington, USA was opened on July 1, 1940. Four months later winds produced a pulsating resultant force in resonance with the natural frequency of the structure.
This caused a steady increase in the amplitude of oscillations until the bridge collapsed. It is for the same reason the marching soldiers break steps while crossing a bridge. Aircraft designers make sure that none of the natural frequencies at which a wing can oscillate match the frequency of the engines in flight! Earthquakes cause vast devastation.
In an earthquake, short and tall structures remain unaffected while the medium height structures fall down. This happens because the natural frequencies of the short structures happen to be higher and those of taller structures lower than the frequency of the seismic waves.
