Kerala Plus One Physics Chapter Wise Previous Questions Chapter 7 Systems of Particles and Rotational Motion
Question 1.
In a hammer throw event, a solid sphere of mass 16 kg is tied to a light 50 cm long chain. A sportsman gives to it a constant moment of 30 N-m for 10 seconds and then throws the sphere. Consider the sphere as a point mass. (MARCH-2010)
a) Find the moment of inertia about the axis of rotation.
b) If L’ is the angular momentum and ‘τ ’ is the torque, show that τ = \(\frac { dL }{ dT }\) .
c) Write an example for the motion in which an angular momentum remains constant.
OR
Remya stands at the center of a turn-table with her two arms “outstretched. The table is set rotating with an angular speed of 40 revolutions/minute.
a) What will happen to the moment of inertia if she folds her hands back?
b) If the angular speed is increased to 100 revolutions/minute, what will be the new moment of inertia?
c) Write the expression for the rotational kinetic energy of the system and explain the terms involved in it.
Answer:

ie The rate of change of angular momentum is the torque applied to it. This is similar to force equal to rate of change of linear momentum,
c) Motion of earth around the sun
OR
a) Moment of inertia decreases
b) If Torque acting on a body is zero, the total angu-lar momentum of a body remains constant.
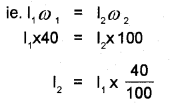
New moment of inertia, l2 = 0.4l1
c) Rotational KE = 1/2lω2
where I is the moment of inertia, a the angular velocity of rotating body.
Question 2.
The moment of inertia of a uniform thin circular disc about a diametrical axis of the disc is where \(\frac{\mathrm{MR}^{2}}{4}\) M is the mass and R is the radius of the disc. (MAY-2010)
a) There is a theorem which helps to find the moment of inertia of the disc about another axis parallel to this axis. Give the statement of this theorem.
b) Using the theorem find the moment of inertia of the disc about a tangential axis in the plane of the disc.
c) A circular disc of mass 0.15kg and radius 0.1 m makes 120 revolutions in one minute about its own axis. Calculate its angular momentum.
Answer:
a) Theorem of parallel axis
The moment of inertia of a body about any axis is equal to the sum of the moment*of inertia of the body about a parallel axis passing through its centre of mass and the product of its mass and the square of the distance between the two parallel axes.
Explanation
Let I be the moment of inertia of a body about an axis AB. Let I0 be moment of inertia about the axis CD parallel to AB and passing through the centre of gravity (G of the body). Let M be the mass of the body and ‘a’ be the distance between the two axes. Then by parallel axes theorem.
L = I0+ Ma2
b) Angular momentum L=Iω
i) Moment of inertia about diameter: It can be found using perpendicular axis theorem.
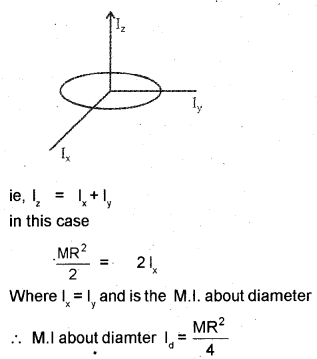
Moment of inertia about tangent: It can be found using parallel axis theorem.
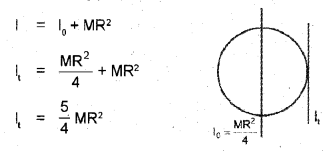
c)
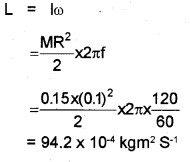
Question 3.
a) The earth revolves around the sun in an elliptical orbit. The closest approach of the earth with the sun is called perihelion. (MARCH-2011)
When the earth approaches the perihelion, its speed increases. Explain this principle.
b) A body rolls over a horizontal, smooth surface without slipping with a translational kinetic energy E.
Show that the total kinetic energy of the body is \(E\left(1+\frac{k^{2}}{R^{2}}\right)\), where k is the radius of gyration and R is the radius of the body. Using the above relation, find the total kinetic energy of a circular disc.
c) A wheel of mass 1000 kg and radius 1 m is . rotating at the rate of 420 rpm. What is the constant torque required to stop the wheel in 14 rotations, assuming the mass to be concentrated at the rim of the wheel?
Answer:
a) Law of conservation angular momentum. Angular mom entum of rotating earth is constant, (ie Iω = constant). When earth approaches the perihelion, moment of inertia (I) decreases. To conserve the angular momentum’ ω ’ increases.
i) Total Kinetic energy,
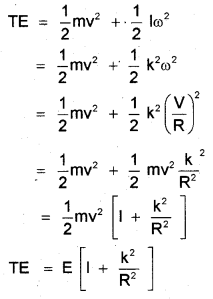
For circular disc I = MK2
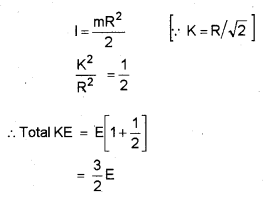
c) Initial angular velocity of wheel, ω1=2πf
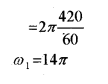
Final angular velocity ω2 = 0
No. of rotations before coming to rest = 14.
Angular displacement before coming to rest θ=14 x 2π
= 28π
We can find angular acceleration from the equation.

Question 4.
Moment of inertia plays the same roll in rotational motion as mass in linear motion. The moment of inertia of a body changes when the axis of rotation changes. (MAY-2011)
a) State the parallel axes theorem on moment of inertia.
b) Write the relation between moment of inertia and angular momentum.
c) If the moment of inertia of a disc about an axis passing through its centre and perpendicular to
its plane is \(\frac{\mathrm{MR}^{2}}{2}\) M is the mass of the disc and R its radius). Determine its moment of inertia about a diameter and about a tangent.
Answer:
a) Theorem of parallel axis
The moment of inertia of a body about any axis is equal to the sum of the moment*of inertia of the body about a parallel axis passing through its centre of mass and the product of its mass and the square of the distance between the two parallel axes.
Explanation
Let I be the moment of inertia of a body about an axis AB. Let I0 be moment of inertia about the axis CD parallel to AB and passing through the centre of gravity (G of the body). Let M be the mass of the body and ‘a’ be the distance between the two axes. Then by parallel axes theorem.
L = I0+ Ma2
b) Angular momentum L=Iω
c) i) Moment of inertia about diameter: It can be found using perpendicular axis theorem.

Moment of inertia about tangent: It can be found using parallel axis theorem.

Question 5.
Rotational inertia is the tendency of a rotating body to resist any change in its state of rotational motion.
a) What do you mean by the radius of gyration of a rolling body? (MARCH-2012)
b) Show that the disc has the moment of inertia I = \(I=\frac{M R^{2}}{2}\) about an axis perpendicular to the disc at its center.
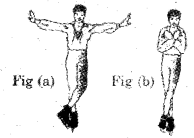
c) In which spinning pose does the ballet dancer have less angular velocity? Justify your answer. different spinning poses of a ballet dancer.
Answer:
a) Radius of gyration, K = \(\sqrt{\frac{l}{M}}\)
b) Out of syllabus
c) Fig (a), In this pose, moment of inertia is larger than the fig (b).
Question 6.
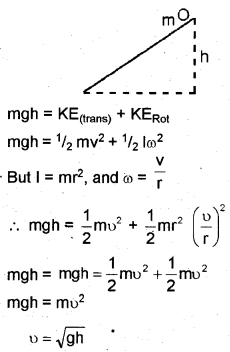
A solid sphere of mass ‘m’ and radius ‘r’ starts from rest and rolls down along an inclined plane as shown. (MAY-2012)
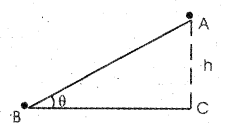
a) Write an expression for the moment of inertia of the sphere about its axis passing through the centre.
b) Why moment of inertia is also called rotational inertia?
c) Find the velocity when it reaches the ground.
Answer:
a) Moment of inertia of solid sphere = \(\frac{2}{5} \mathrm{MR}^{2}\)
b) Moment of inertia is a measure of rotational inertia. Hence moment of inertia is called rotational inertia.
c)
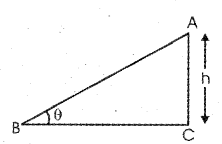
If a solid sphere of mass ‘m’ and radius ‘r’ reaches at ground from a height h, potential energy (PE) is converted in to rotational KE and translational KE.
ie, PE= Rotational KE + translational KE

Question 7.
In an experiment with a bicycle rim, keeping the rim in the vertical position with both the strings in one hand, put the wheel in fast rotation (see figure.) When string B is released, the rim keeps rotating in a vertical plane and the plane of rotation turns around the string A. (MARCH-2013)
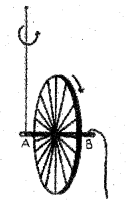
a) Mention the lawthat explains the above result.
b) Explain the practical example (shown in the figure) based on the law mentioned in a).

c) How will you distinguish a hard boiled egg and a raw egg by spinning each on a table top?
d) A solid cylinder of mass 20 kg rotates about its axis with an angular speed of 100 rad s-1. The radius of the cylinder is 0.25 m. What is the magnitude of angular momentum of the cylinder about its axis?
Answer:
a) Conservation of angular momentum
b) If a girl rotating with a uniform speed on turn table,
its angular momentum (L = Iω) will be a constant. When she suddenly stretches her hand, I increases and ω decreases to keep L as constant.
c) The egg which spins faster will be hard boiled egg. In the case of a raw egg, the liquid matter in the egg tries to get away from axis of rotation, thereby increasing its moment of inertia. As M.l is more, raw egg will spin with lower angular acceleration (provided same torque is applied in both the cases to set them spinning).
d)

Question 8.
Moment of inertia is the analogue of mass in rotational motion. But unlike mass, it is not a fixed quantity. (MARCH-2014)
a) Moment of inertia can be regarded as a measure of rotational inertia. Why?
b) State any two factors on which the moment of inertia of a rigid body depends.
c) The moments of inertia of two rotating bodies A and B are lA and lB (lA > lB) and their angular mo-mentum are equal. Which one has a greater kinetic energy? Explain.
Answer:
a) The rotational inertia depends on mass of the body and axis of rotation. In otherwords it depends on moment of inertia.
b) Mass – M
Radius of rotation – R
c)
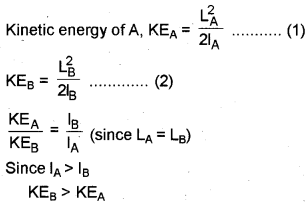
Body B has more kinetic energy compared to A.
Question 9.
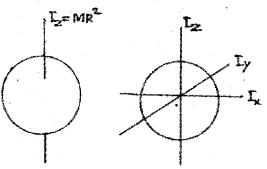
Moment of inertia of a ring about an axis passing through the center is MR2. The moment of inertia about a diameter can be found using the perpendicular axis theorem. (MAY-2014)
a) State the perpendicular axis theorem.
b) Obtain the expression for the moment of inertia of a ring about its diameter.
Answer:
a) The moment of inertia of plane lamina about z- axis is equal to sum of the moments of inertia about x axis and y axis; if lamina lies in xy plane.
b)
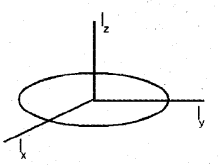
According to perpendicular axis theorem,
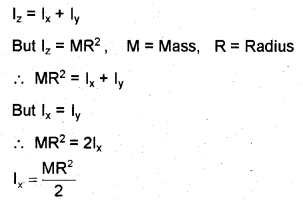
Ix is the moment of inertia of ring about diameter,
Question 10.
Moment of inertia is the rotational analogue of mass,in linear dynamics. (MARCH-2015)
a) Write the equation of the moment of inertia of a disc about an axis passing through its center and perpendicular to its plane.
b) State the parallel axis theorem of moment of inertia.
c) A coin is rolling on a plane surface. What fraction of its total kinetic energy is rotational?
Answer:
a) I = \(\frac{m r^{2}}{2}\)
b) Theorem of parallel axis
The moment of inertia of a body about any axis is equal to the sum of the moment*of inertia of the body about a parallel axis passing through its centre of mass and the product of its mass and the square of the distance between the two parallel axes.
Explanation
Let I be the moment of inertia of a body about an axis AB. Let I0 be moment of inertia about the axis CD parallel to AB and passing through the centre of gravity (G of the body). Let M be the mass of the body and ‘a’ be the distance between the two axes. Then by parallel axes theorem.
L = I0+ Ma2
c) Total energy, T.E = Translational KE + Rotational
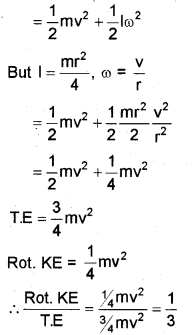
Question 11.
A rigid body is a body with a perfectly unchanging shape under the influence of an external force. What do you mean by the center of mass of a rigid body? (MARCH-2015)
Answer:
Centre of mass of a body is a point at which the whole mass is assumed to be concentrated.
Question 12.
a) State perpendicular axis theorem. Use this theorem to find moment of inertia of a ring about its diameter. (MAY-2015)
b) Two identical concentric rings each of mass M and radius R are placed perpendicular to each other. What is the moment of inertia about an axis passing through the center of this system?
![]()
OR
a) Derive the mathematical relation between angular momentum and torque. State the law of con-servation of angular momentum.
b) A solid sphere is rotating about a diameter at an angular velocity ω . If it cools so that its radius reduces to \(\frac { 1 }{ n }\) of its original value, its angular velocity becomes….

Answer:
a) Moment of inertia of a plane lamina about the z- axis is equal to sum of the moments of inertia about x-axis and y axis, if planar lamina lies in x- y plane.
lz = lx+ly
Moment of inertia of ring about one of its diameter
According to perpendicular axis theorem,

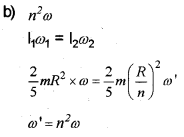
Question 13.
a) Classical dancers bring their hands closer to their employed by them. (MAY-2016)
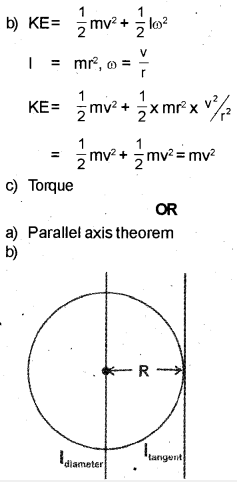
b) A wheel rolls along a straight line. Derive an expression for its total kinetic energy.
c) The rotational analogue of force is ………
OR
moment of inertia about diameter of a ring is \(I_{0}=\frac{M R^{2}}{2}\)
Name the theorem that helps to find the moment of interia about a tangent parallel to the diameter.
b) Draw a diagram and find the moment of interia about a tangent, parallel to the diameter of the ring.
c) The rotational analogue of mass is ………..
Answer:
a) Conservation of angular momentum
Consider a ring of mass M and radius R. If this ring is rotating about tangent, we can use parallel axis theorem.
According to parallel axis
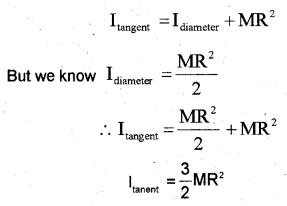
c) Moment of interia
Question 14.
The rotational analogue of force is moment of force, also called torque. (MARCH-2016)
a) The turning effect of force is maximum when the angle between \(\overrightarrow{\mathrm{r}}\) and \(\overrightarrow{\mathrm{F}}\) is…
b) A wheel starting form rest acquires an angular velocity of 10 rad/s in two seconds. The moment of inertia of the wheel is 0.4 kg m². Calculate the torque acting on it.
c) The possibility of falling backward with the ladder is more when you are high upon the ladderthan when you just begin a climb. Explain why.
Answer:
a) 9o°
b)
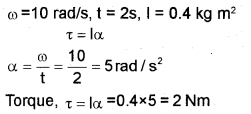
c) When a person is high up on the ladder, ‘r’ is large and hence even a small force can make the ladder fall. When a person just begins to climb r is small, heavy force is required to make the ladder fall.
Question 15.
The demonstration of conservation of angular momentum is schematically shown in the figures. (MARCH-2017)
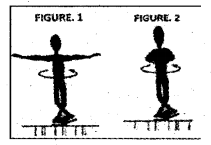
Identify the figure which has more angular velocity.
Answer:
Figure 2
Question 16.
The angular momentum of a particle is the rotational analogue of its linear momentum. (MARCH-2017)
a) The equation connecting angular momentum and linear momentum is….
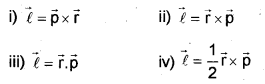
b) Starting from the equation connecting angular momentum and linear momentum, deduce the relation between torque and angular momentum.
OR
Moment of inertia in rotational motion is analogus to mass in linear motion.
a) The moment of inertia of a circular disc about an axis perpendicular to the plane, at the centre is given by….
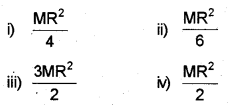
State perpendicular axis theorem and by using the theorem, deduce the moment of inertia of the circular disc about an axis passing through the diameter.
Answer:
a) ii, \(\overrightarrow{\mathrm{l}}\) = \(\overrightarrow{\mathrm{r}}\) x \(\overrightarrow{\mathrm{p}}\)
b) If Torque acting on a body is zero, the total angular momentum of a body remains constant.
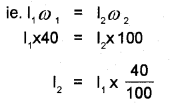
New moment of inertia, l2 = 0.4l1
OR
a) iv \(\frac{\mathrm{MR}^{2}}{2}\)
b) Perpendicular axis theorem

According to the perpendicular axis theorem,
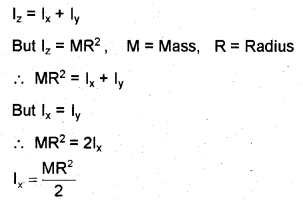
Ix is the moment of inertia of ring about diameter,
Question 17.
Say True or False : (MAY-2011)
The location of centre of mass of a system is independent of the frame of reference used to locate it.
Answer:
True
Question 18.
A thin circular ring is rotating about an axis. (MAY-2013)
a) State the theorem which will help you to find the moment of inertia about its diameter.
b) Using this theorem, find the moment of inertia of the ring about its diameter.
c) A ring rolls down the inclined plane without slipping. Find the velocity of the ring when it reaches the ground.
Answer:
a) Perpendicular axis theorem
b)

According to the perpendicular axis theorem,
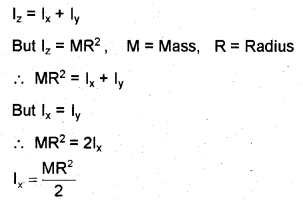
Ix is the moment of inertia of ring about diameter,
c) When a ring of mass ‘m’ rolls down from a height h, potential energy converts into translational kinetic energy and rotational kinetic energy.
When the body reaches at the bottom,