Kerala Plus One Physics Chapter Wise Previous Questions Chapter 14 Oscillations
Question 1.
The motions that repeat themselves are called periodic motions but for a simple harmonic motion, the force must be proportional to the displacement and it is directed towards the centre of motion. [March -2010]
(a) Write an example for a periodic motion that is not simple harmonic.
(b) Write the expression for a period of oscillation of:
(i) a loaded spring
(ii) a simple pendulum
(c) A particle executes a SHM of amplitude ‘a’.
(i) At what distance from the mean position is its kinetic energy equal to its potential energy?
(ii) At what points is its speed half the maximum speed?
Answer:
(a) Revolution of earth around the sun.

Question 2.
The amplitude of a simple harmonic oscillation is doubled. What change will you observe in the following physical quantities of the oscillator ? [May -2010]
(a) Period
(b) Maximum velocity
(c) Maximum acceleration
(d) Total energy.
Answer:
(a) No change
(b) Becomes double (Vmax = Aω)
(c) Becomes double amax = Aω2
(d) Becomes 4 times (E = Vi mω2A2)
Question 3.
(a) A simple pendulum is an object suspended by a weightless and inextensible string fixed rigidly to a support.
(i) Under what conditions for the amplitude, are the oscillations of the pendulum simple harmonic? [March – 2011]
(ii) The period of oscillation of the pendulum is T.
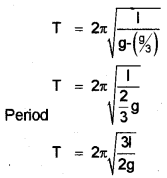
What will be the period if the pendulum is suspended in a lift moving down with an acceleration equal to g/3.
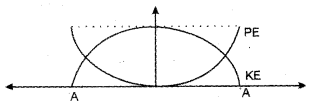
(b) A particle executing SHM possess both potential energy and kinetic energy. During the oscillation, the total energy remains constant. If A is the amplitude of oscillation of the particle,
(i) Show graphically, the variation of potential energy and kinetic energy with displacement.
(ii) At what displacement are these energies equal?
Answer:
(a) (i) Amplitude should be small|
(ii) The period of simple pendulam,
\(\mathrm{T}=2 \pi \sqrt{\frac{1}{\mathrm{~g}}}\)
(b)
Question 4.
The amplitude of oscillation of a simple pendulum oscillating in air decreases continuously. This is because of damping. If the damping force is proportional to the veloity of the oscillator, derive an expression for its frequency. [May – 2011]
OR
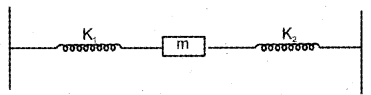
Two springs of force constant ‘K1’ and ‘K2. are connected to a mass ‘m’ placed on a horizontal frictionless surface as shown in the figure. Derive an expression for the time period of the horizontal oscillation of the system.
Answer:
The damping force Fd a- v (or) Fd = -bv where b is called damping constant.
The restoring force due to spring. Fs – -kx. where x is the displacement of the mass from its equilibrium position.
Total force on the block, F = -bv + -kx
ma = -bv + -kx
ma + bv + kx = 0
\(\mathrm{m} \frac{\mathrm{d}^{2} \mathrm{x}}{\mathrm{dt}^{2}}+\mathrm{b} \frac{\mathrm{d} \mathrm{x}}{\mathrm{dt}}+\mathrm{kx}=0\)
This is the differential equation of S.H.M.
The solution of the above differential equation of damped harmonic oscillator is
\(x(t)=\mathrm{Ae}^{-b / 2 \mathrm{~m}} \cdot \cos \left(\omega^{1} t+\phi\right) . \text { Where } \mathrm{Ae}^{\frac{-b t}{2 \mathrm{~m}}}\) amplitude and ω1 is the angular frequency of the damped oscillator.
\(\omega^{1}=\sqrt{\frac{\mathrm{k}}{\mathrm{m}}-\frac{\mathrm{b}^{2}}{4 \mathrm{~m}^{2}}}\)
OR
(Out of syllabus).
Consider a body of mass ‘m’ suspended by means of two springs of force constant K1 and K2 connected in parallel. Let the mass ‘m’ be pulled down through a distance ‘x’ by a force F. Both springs get extended through the same distance‘x’.
Restoring force in 1st spring = ‘K1 x
Restoring force in 2nd spring = ‘K2 x
Total restoring F = – (K1 + K2) x

Question 5.
Say True or False:
Greaterthe mass of the pendulum bob shorter is its frequency of oscillation.
Answer:
False
Question 6.
Oscillations of a loaded spring are spring are simple harmonic motion. [March – 2012]
- What do you mean by simple harmonic motion?
- Derive and expression for period of oscillation of a loaded spring.
- A body oscillates with S.H.M. is given by \( x=5 \cos \left[2 \pi t+\frac{\pi}{4}\right]\)
Calculate the displacement at time, t = 1,5s
Answer:
The oscillatory motion is said to be simple harmonic motion if the displacement ‘x’ of the particle from the origin varies with time as. x(t) = A Cos (ωt + φ)
(b)
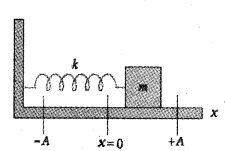
Consider a body of mass m attached to a massless spring of spring constant K. The other end of spring is connected to a rigid support as shown in figure. The body is placed on a frictionless horizontal surface. If the body be displaced towards right through a small distance Y, a restoring force will be developed.

Question 7.
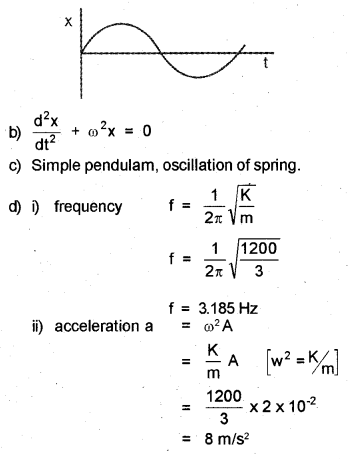
(a) Represent Simple Harmonic Motion graphically. [May – 2012]
(b) Write the differential equation representing Simple Harmonic Motion.
(c) Name two examples forsimple harmonic motion.
(d) A spring with spring constant 1200 N/m is mounted on a horizontal table as shown. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2 cm and released.
Determine:
(i) Frequency of Oscillations.
(ii) Maximum acceleration of the mass.
Answer:
Question 8.
(a) What is a seconds pendulum?
(b) Time period of a particle in SHM is \(\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{k}}}\)
A simple pendulum executes SHM approximately. Why then is the time period of pendulum is independent of mass?
(c) What is the frequency of oscillation of a simple pendulum mounted in a cabin that is freely falling undergravity.
Answer:
(a) A pendulam having period 2 sec is called seconds pendulam.
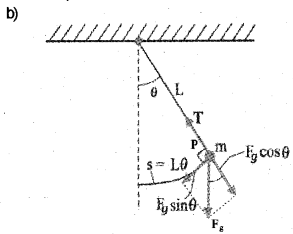
Consider a mass m suspended from one end of a string of length L fixed at the other end as shown in figure. Suppose P is the instantaneous position of the pendulum. At this instant its string makes an angle 0 with the vertical.
The forces acting on the bob are (1) weight of bob Fg (mg) acting vertically downward. (2) Tension T in the string.
The gravitational force Fg can be divided into a radial component FgCosθ and tangential component FgSinθ. The tangential component FgSinθ produces a restoring torque.
Restoring torque τ = – Fg sin θ . L.
τ = -mg sinθ . L ——————— (1).
-ve sign shown that the torque and angular displacement θ are oppositely directed. For rotational motion of bob.
τ = lα ——————— (2).
Where I is moment of inertia about the point of suspension and α is angular acceleration. From eq (1) and eq (2).
lα = – mg sinθ . L
If we assume that the displacement θ is small, sin θ ≈ θ
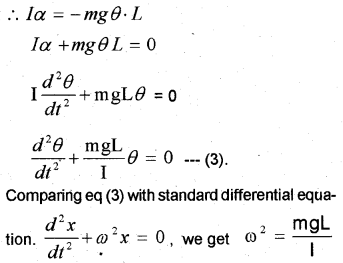

Question 9.
The motion represented by the equation y(t) = A Cos (ωt + φ) is called simple harmonic motion (SHM).[March -2012]
(a) Which one of the following examples closely represents SHM? Substantiate your answer.
(i) The rotation of the earth about its axis.
(ii) Oscillations of a swing.
(b) A vibrating simple pendulum of period T is placed in a lift which is accelerating downwards. What is the effect of this on the time period of the pendulum?
(c) The displacement of y (in cm) of an oscillating particle varies with time t (in sec) according to the equation.
y = 2 Cos (0.5 πt + π/3)
Find the amplitude and period of the particle.
Answer:
(a) Oscillation of a swing
Oscillation obeys the relation F α – x
(b) When pendulam is placed in a lift, which is accelerating dowards
peroid \(\mathrm{T}=2 \pi \sqrt{\frac{\ell}{\mathrm{g}-\mathrm{a}}}\)
The above equation shows that period of oscillation increases,
(c) y = 2 Cos (0.5 πt +π/3)
When we compare this equation with standard equation

Question 10.
Simple Pendulum is an example for a harmonic oscillator. [May -2013]
(a) Define Simple Harmonic Motion.
(b) What is the expression for the period of oscillation of a simple pendulum?
(c) A girl is swinging on a swing in the sitting position. How will the period of swing be affected if she stands up?
Answer:
The oscillatory motion is said to be simple harmonic motion if the displacement ‘x’ of the partide from the origin varies with time as
x(t) = A cost(ωt + φ)
OR
A partide is said to be execute simple harmonic motion when it vibrates periodically in such a way that at any instant the force ading on it is directly proportional to the displacement from a fixed point in its path and is always directed towards that fixed point.
(b) \(\mathrm{T}=2 \pi \sqrt{\frac{\ell}{\mathrm{g}}}\)
(c) Period of oscillation decreases. When girl stands up, the effective length of pendulum decreases. As a result period of pendulum decreases.
Question 11.
A simple pendulum starts with its bob at position X, shown in the figure. The bob is pulled aside to Y and then released. It swings from Y to Z and back to Y. [March – 2014]
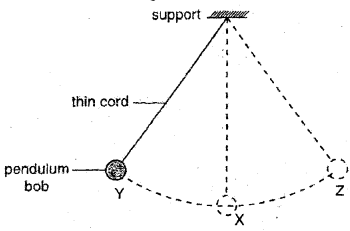
(a) Take suitable words from the bracket and fill in the gaps.
(potential, constant, kinetic, different, work, resonance)
To move the bob from X to Y,………………… has to be done on it and its…………………. energy increases. As it moves from Y to X, some of this energy is converted to ……………… energy. Throughout the swing from Y to Z and back to Y, the total energy is …………………
(b) What is the acceleration of the bob when it is at
(c) What are damped oscillations?
Answer:
(a)
- Work
- Potential energy
- Kinetic energy
- Constant
(b) zero
(c) Periodic oscillations of decreasing amplitude due to the presents of resistive force of the medium are called damped oscillation.
Question 12.
Time period of a particle in simple harmonic motion (SHM) depends on the force constant K and mass m of the particle. [May – 2014]
(a) A simple pendulum executes SHM approximately. Why then is the time period of a simple pendulum independent of the mass of the pendulum?
(b) A man with a wristwatch on his hand falls from the top of a tower. Does the watch give the correct time during the free fall? Why?
(c) What is the frequency of a simple pendulum mounted in a cabin that is freely falling under gravity?
Answer:
(a) Period of simple pendulum \(\mathrm{T}=2 \pi \sqrt{\frac{1}{\mathrm{~g}}}\)
This equation shows that period is independent of mass of pendulum.
(b) Wrist watch works based on the energy stored in the spring or battery. This energy does not change during its free fall. Hence watch shows correct time during free fall.
(c) Frequency of simple pendulum under free fall
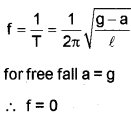
Question 13.
(a) A particle executing SHM is an example of …………. [March -2015]
(i) acceleration of constant magnitude and direction.
(ii) acceleration of changing magnitude and direction.
(iii) acceleration of changing magnitude but constant direction.
(iv) acceleration of constant magnitude but changing direction.
(b) List any two conditions for a motion of a body to be simple harmonic.
(c) An SHM is given by x = 8Sin(1(kt + 7t/4)m. At which position will its kinetic energy become equal to its potential energy?
x = 8Sin(107πt + π/4)m
Answer:
(ii)
(b) Simple harmonic motion is the simplest form of oscillatory motion.
The oscillatory motion is said to be simple harmonic motion if the displacement ‘x’ of the particle from the origin varies with time as

Question 14.
(a) Write the mathematical expression for the period of simple pendulum. Drive it. [May – 2015]
(b) The time period of a simple pendulum of length L as measured in a lift descending with the acceleration \(\frac{g}{3} m / s^{2}\)
Answer:
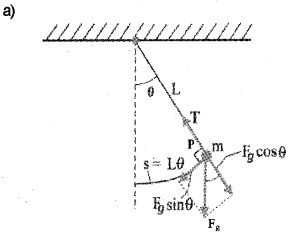
Consider a mass m suspended from one end of a string of length L fixed at the other end as shown in figure. Suppose P is the instantaneous position of the pendulum. At this instant its string makes an angle θ with the vertical.
The forces acting on the bob are (1) weight of bob Fg (mg) acting vertically downward. (2) Tension T in the string.
The gravitational force Fg can be divided into a radial component FgCosθ and tangential component FgSinθ. The tangential component FgSinθ produces a restoring torque.
Restoring torque τ = – Fg sinθ – L .
τ = -mg sinθ . L —— (1).
-ve sign shown that the torque and angular displacement 0 are oppositely directed. For rotational motion of bob,
τ = lα — (2).
Where I is moment of inertia about the point of suspension and α is angular acceleration. From eq (1) and eq (2).
I α= -mg sinθ -L
If we assume that the displacement θ is small, sin θ ≈ θ.


Question 15.
Motion of a simple pendulum is an example for simple harmonic motion. [March -2016]
(a) What do you mean by simple harmonic motion?
(b) The acceleration due to gravity on the surface of the moon is 1.7 m/s2. What is the time period of a simple penduium on the moon, if its time period on the earth is 3.5 second? Answer:
(a) The oscillatory motion is called simple harmonic, if the displacement ‘x’ of the particle form the origin various with time as x(t) = Acos(cot+φ)
(b) g=1.7m/s2, Te = 3.5s, ge = 9.8m/s2
\(T_{e}=2 \pi \sqrt{\ell / g} \ldots . .(1)\)

Question 16.
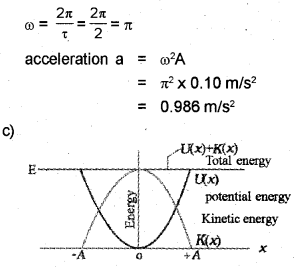
(a) Define Simple Harmonic Motion (SHM). [May – 2016]
(b) For a SHM, time period T = 2s. If displacement from the mean position is 10cm, calculate the instantaneous acceleration.
(c) Graphically show the variation of Kinetic energy of a simple pendulum in SHM with its position.
Answer:
(a) The oscillatory motion is said to be simple harmonic motion if the displacement ‘x’ of the particle from the origin varies with time as Px(t) = A cos(wt+θ)
(b) T = 2s,A= 10cm = 0.10m
Question 17.
(a) Among the following, which are the examples of simple harmonic motion? [March -2017]
i. The rotation of earth about its axis.
ii. Vertical oscillations of a loaded spring.
iii. Oscillations of simple pendulum.
iv. Uniform circular motion
(b) The displacement in simple harmonic motion can be represented as x(t)=A cos( ωt + φ), where ‘ φ ’ is the phase constant.
Identify and define ‘A’ and ‘ ω ’ in the equation.
Answer:
(a)
(ii) vertical oscillations of loaded spring
(iii) Oscillations of simple pendulum
(b) A is amplitude. It is the maximum displacement, ω is angular velocity. It is defined as rate of change of angulardisplacement \(\omega=\frac{d \theta}{d t}\)
