Kerala Plus One Physics Chapter Wise Previous Questions Chapter 12 Thermodynamics
Question 1.
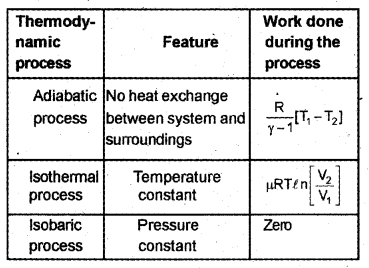
Match the following: (MARCH-2010)

Answer:

Question 2.
Thermodynamics deals with the concept of heat and the exchange of heat energy. (MARCH-2010)
a) Which law of thermodynamics is used to explain the working of heat engine?
b) What are the sink, source and working substances of a domestic refrigerator?
c) Explain briefly, the operations of a Carnot’s engine, draw the Carnot’s cycle and deduce the expression for its efficiency.
OR
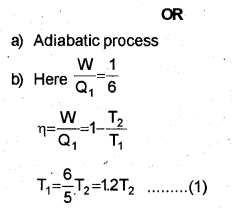
a) Which thermodynamic process is also called an isoentropic process?
b) The efficiency of a Carnot engine is \(\frac { 1 }{ 6 }\) If on reducing the temperature of the sink by 65°C, its efficiency becomes \(\frac { 1 }{ 3 }\) find the temperature of the sink and the source.
c) Obtain the expression for the work done during an adiabatic process.
Answer:
a) Second law of thermodynamics
b) sink – contents of refrigerator
source – Atmosphere
working substance – Freon gas
c) Carnot’s cycle
The Carnot cycle consists of two isothermal processes and two adiabatic processes.

Let the working substance in Carnot’s engine be the ideal gas.
Step 1 : The gas absorbs heat Q1 from hot reservoir at T, and undergoes isothermal expansion from (P1, V1 ,T1) to (P2, V2, T1).
Step 2 : Gas undergoes adiabatic expansion from (P2, V2, T1) to (P3,V3, T2)
Step 3 : The gas release heat Q2 to cold reservoir at T2, by isothermal compression from (P3,V3,T2)to(P4,V4,T2).
Step 4: To take gas into initial state, work is done on gas adiabatically (P4, V4, T2) to (P1, V1, T1)
Efficiency of Carnot’s engine
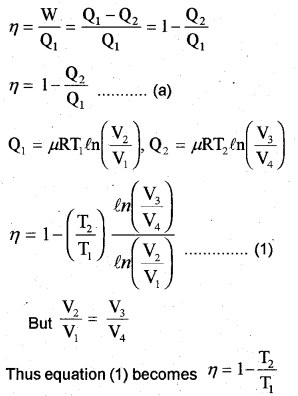
When the temperature of sink is decreased by 65°C (or 65K), efficiency becomes double. Let T21 be the reduced temperature of sink.
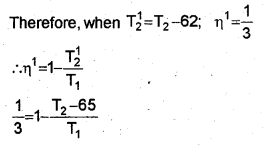
Substitute the value eq. in eq., we get
T1= 1.2 x 325 = 390K
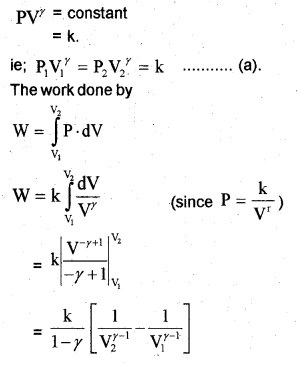
c) Work done by adiabatic process
Let an ideal gas undergoes adiabatic charge from (P1, V1,T1) to (P2, V2, T2). The equation for adiabatic charge is

Question 3.
The increase in dimensions of a body due to increase in temperature is called thermal expansion. (MAY-2010)
a) The ratio among the coefficients of linear expansion, area expansion and volume expansion is ………..
b) Railway lines are laid with gaps to allow for expansion. If the gap between steel rails 60 m long is 3.63 cm at 10° C, then at what temperature will the lines just touch ? Coefficient of linear expansion for steel is 11 x 10 -6/oC.
OR
Modulus of elasticity of a material is the ratio of stress and strain.
a) Young’s modulus for a perfectly rigid body is ………
b) One end of a rope of length 4.5 m and diameter6 mm is fixed to the branch of a tree. A monkey weighing 100 N jumps to catch the free end and stays there. Find the elongation of the rope (Young’s modulus = 4.8×1011 N/m2)
Answer:
a) 1:2:3

Question 4.
A heat engine is a device which converts heat energy into mechanical energy. Carnot designed an ideal heat engine which uses an ideal gas as working substance. (MAY-2010)
a) Draw a graph showing the variation of pressure and volume of the. working substance during the operations of this engine in one cycle.
b) A Carnot engine working between 527° C and 127° C has a work output of 800 J per cycle. How much heat is supplied to the engine from the source per cycle ?
Answer:
Work done by adiabatic process
Let an ideal gas undergoes adiabatic charge from (P1, V1,T1) to (P2, V2, T2). The equation for adiabatic charge is


Question 5.
a) Isothermal, isobaric, isochoric and adiabatic processes are some special thermodynamic processes. In which of these processes, the work done is maximum, when a gas expands from V1 to V2? (MARCH-2011)
b) Which law of thermodynamics implies that no heat engine can be 100% efficient?
c) One mole of an ideal gas expands from volume V1 to volume V2 at a constant temperature T. Derive an expression for the work done.
Answer:
a) Isobaric process
b) Second law of thermodynamics
c) For an isothermal process, the equation of state is
PV = constant
= μRT
p = \(\frac { μRT }{ V }\)
Let a system undergoes an isothermal process at temperature T, from the state (P1, V1) to (P2, V2).
Let ‘∆V’ be a small charge in volume due to pressure P.
Then work done (for ∆V )
∆W = P∆Y.

Question 6.
A heat engine is a device that converts heat energy into mechanical energy. (MAY-2011)
a) Briefly explain the working of a heat engine taking Carnot engine as an ideal engine.
b) A refrigerator is a reverse heat engine. Can we decrease the temperature of a room by keeping the door of a refrigerator opened? Explain.
Answer:
a) Carnot’s cycle
The Carnot cycle consists of two isothermal pro-cesses and two adiabatic processes.

Let the working substance in Carnot’s engine be the ideal gas.
Step 1 : The gas absorbs heat Q1 from hot reservoir at T1 and undergoes isothermal expan-sion from (P1, V1, T1) to (P2, V2, T1).
Step 2 : Gas undergoes adiabatic expansion from(P2,V2,T1)to(P3,V3,T2)
Step 3 : The gas release heat Q2 to cold reservoir at T2, by isothermal compression from
(P3,V3,T2)to(P4,V4,T2).
Step 4: To take gas into initial state, work is done on gas adiabatically [(P4, V4, T2) to (P1, V1, T1)]
b) No. Suppose that the refrigerator draws some heat from the air in front of it. The compressor has to do some mechanical work (at the expense of elec-trical energy) to draw heat from the air at lower temperature. The heat drawn from the air together with the work done by the compressor in drawing it, is rejected by the refrigerator with the help of radiator (provided at the back) to the air.
In each cycle, the amount of heat rejected to the air (at the back of refrigerator) will be greater than that is drawn from the air (in front of it). Therefore the temperature inside the room will increase.
Question 7.
A heat engine is a device which converts heat energy into work. (MARCH-2012)
a) What is the working substance in an ideal heat engine?
b) Draw the Carnot cycle and explain its working.
c) Calculate the efficiency of an engine working between steam point and ice point. Can you design an engine of 100% efficiency?
Answer:
a) Ideal gas or perfect gas.
b) Carnot’s cycle
The Carnot cycle consists of two isothermal pro-cesses and two adiabatic processes.

Let the working substance in Carnot’s engine be the ideal gas.
Step 1 : The gas absorbs heat Q1 from hot reservoir at T1 and undergoes isothermal expan-sion from (P1, V1, T1) to (P2, V2, T1).
Step 2 : Gas undergoes adiabatic expansion from(P2,V2,T1)to(P3,V3,T2)
Step 3 : The gas release heat Q2 to cold reservoir at T2, by isothermal compression from
(P3,V3,T2)to(P4,V4,T2).
Step 4: To take gas into initial state, work is done on gas adiabatically [(P4, V4, T2) to (P1, V1, T1)]
c)

Question 8.
Three moles of an ideal gas kept at a constant temperature of 300 K are compressed from the volume of 10 litre to 5 litre. (MAY-2012)
a) Which thermodynamic process is involved in this, process?
b) Calculate the work done required to compress this gas.
Answer:
a) Isothermal process
b) Work done = 2.303 nRT log\(\frac { V2 }{ V1 }\)
= 2.303 x 3 x 8.3 x 300 x log102
= 2.303 x 3 x 300 x 8.3 x 0.3010
= 5178J
Question 9.
Figure given below depicts the schematic representation of an engine. (MARCH-2013)
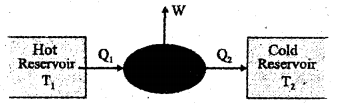
a) Which type of engine is this, a heat engine or a refrigerator?
b) Write the 4 steps of operation in the Carnot cycle.
c) A Carnot engine is working between temperatures of 27°C and 327°C. Find its efficiency (η)
Answer:
a) heat engine
b) The Carnot cycle consists of two isothermal processes and two adiabatic processes.
1) Isothermal expansion
2) Isothermal compression
3) Adiabatic expansion
4) Adiabatic compression
T1 = 327°C = 600 K
T2 = 27°C = 300 K
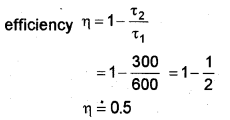
Question 10.
P-V diagram of a gas is shown in the figure. In this figure AB represents isobaric process and AD represents isothermal process. (MAY-2015)
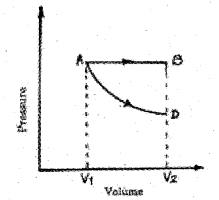
a) Explain isobaric process and isothermal process.
b) Using the above graph, find the process in which the work done is maximum. Give the reason.
Answer:
a) The thermodynamic process at constant pressure is called isobaric process. Thermodynamic process at constant temperature is called isothermal process.
b) The work done is maximum for AB because area under AB is more than that of AD.
Question 11.
a) Heat engine is a device used to convert ……. energy into ……… energy. (MARCH-2016)
b) Name the four processes taking place in Carnot cycle.
Draw indicator diagram of Carnot cycle.
c) A hole is drilled in a copper sheet. The diameter of the hole is 4.24 cm at27°C. What is the change in diameter of the hole when the sheet is heated to 227°C? (Coefficient of linear expansion of cop- per=1.7 x 10-5/°C.)
Answer:
a) heat, mechanical
b) Isothermal expansion, adiabatic expansion, isothermal compression and adiabatic compression.
Work done by adiabatic process
Let an ideal gas undergoes adiabatic charge from (P1, V1,T1) to (P2, V2, T2). The equation for adiabatic charge is


c) The coefficient of linear expansion, αl = 1.7 x 10
Initial diameter, l = 4.24 cm
Initial temperature, Ti = 27°C .
final temperature, Tf = 227°C
∆T = 227 – 27= 200°C
αl = \(\frac { ∆l }{ l∆T }\)
∆l = l.∆T x αl
= 4.24 x 200 x 1.7 x 10-5
= 0.014cm
Question 12.
a) What is the difference between isothermal and adiabatic processes? (MAY-2016)
b) Explain Carnot’s cycle.
c) Write the expression for the efficiency of a Carnot engine.
Answer:
a) In isothermal process temperature remains constant. In adiabatic process net heat flow is zero (heat constant)
b) Carnot’s cycle
The Carnot cycle consists of two isothermal pro-cesses and two adiabatic processes.

Let the working substance in Carnot’s engine be the ideal gas.
Step 1 : The gas absorbs heat Q1 from hot reservoir at T1 and undergoes isothermal expan-sion from (P1, V1, T1) to (P2, V2, T1).
Step 2 : Gas undergoes adiabatic expansion from(P2,V2,T1)to(P3,V3,T2)
Step 3 : The gas release heat Q2 to cold reservoir at T2, by isothermal compression from
(P3,V3,T2)to(P4,V4,T2).
Step 4: To take gas into initial state, work is done on gas adiabatically [(P4, V4, T2) to (P1, V1, T1)]
c) η = 1 – T2 /T1
Question 13.
“Two systems in thermal equilibrium with a third system, are in thermal equilibrium with each other”. Identify the law given by the above statement. (MARCH-2017)
Answer:
Zeroth law of thermodynamics
Question 14.
Match the following in three columns. (MARCH-2017)
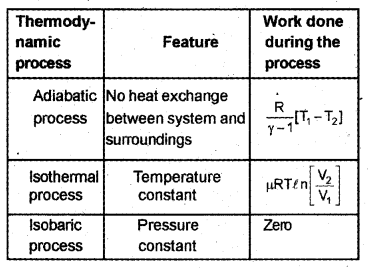
Answer: