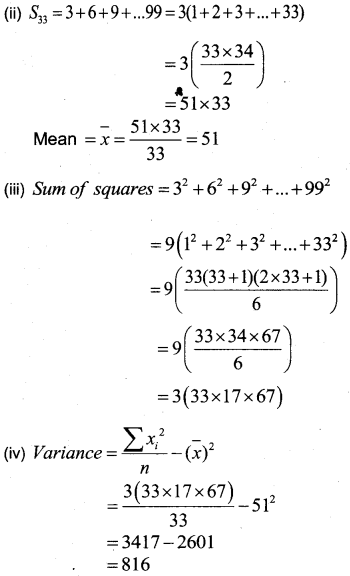Kerala Plus One Maths Previous Year Question Paper March 2019 with Answers
| Board | SCERT |
| Class | Plus One |
| Subject | Maths |
| Category | Plus One Previous Year Question Papers |
Time Allowed: 2 1/2 hours
Cool off time: 15 Minutes
Maximum Marks: 80
General Instructions to Candidates :
- There is a ‘cool off time’ of 15 minutes in addition to the writing time.
- Use the ‘cool off time’ to get familiar with the questions and to plan your answers.
- Read instructions carefully.
- Read questions carefully before you answering.
- Calculations, figures and graphs should be shown in the answer sheet itself.
- Malayalam version of the questions is also provided.
- Give equations wherever necessary.
- Electronic devices except non programmable calculators are not allowed in the Examination Hall.
Answer any 6 from questions 1 to 7. Each question carries 3 score. (1 × 6 = 6)
Question 1.
Let A = {x: x is a prime number less than 11} and B = {x: x is an integer such that 2 ≤ x ≤ 8}.
(i) Write C = A ∩ B.
(ii) Find the number of subsets of C which has 3 elements.
(iiii) What is the probability of getting a subset of 3 elements from the power set of C.
Answer:
(i) A = {2, 3, 5, 7}; B = {2, 3, 4, 5, 7, 8}
C = {2, 3, 5, 7} ∩ {2, 3, 4, 5, 7, 8} = {2, 3, 5, 7}
(ii) Number of subsets of C which has 3 elements
= 4C3 = 4
(iii) Probability of getting a subset of 3 elements from the power set of C
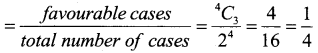
Question 2.
(i) Find(a + b)4 -(a – b)4.
(ii) Hence evaluate
(√3 + √2)4 – (√3 – √2)4.
Answer:
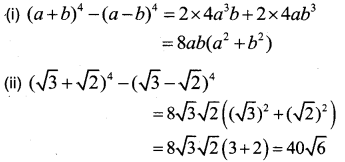
Question 3.
Find the square root of the complex number 3 + 4i.
Answer:
Let x + iy = √3+4i
Then (x + iy)2 = 3 + 4i
⇒ x2 – y2 + 2xyi = 3 + 4i
Equating real and imaginary parts, we have
x2 – y2 = 3 ……… (1)
2xy = 4
We know the identity
(x2 + y2)2 = (x2 – y2)2 + (2xy)2
= 9 + 16 = 5
Thus, x2 +y2 = 5 …….. (2)
From (1) and (2), x2 = 4 and y2 = 1 or x = ±2 and y = ±1
Since the product xy is positive,
we have x = 2, y = 1 or, x = – 2, y = -1
Thus, the square roots of 3 + 4i are
2 + i and -2 – i.
Question 4.
The sum of first three terms of a Geometric Progression is 1312 and their product is -1. Find the common ratio and the terms.
Answer:
Let ar, a, ar be the numbers.
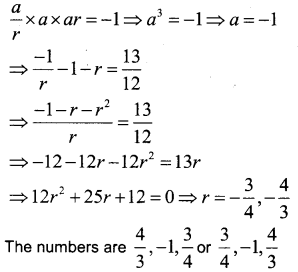
Question 5.
Find the solution of the equation
sinx + sin3x + sin5x = 0
Answer:
sinx + sin3x + sin5x = 0
2 sin3x cos2x + sin3x = 0
⇒ sin3x (2 cos2x + 1) = 0
⇒ sin 3x = 0; 2 cos 2x + 1 = 0
⇒ 3x = nπ, n ∈ Z; 2 cos2x = -1
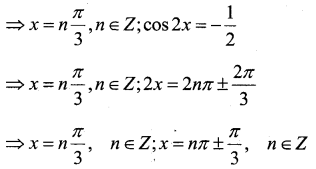
Question 6.
Consider the graph of the function f(x)
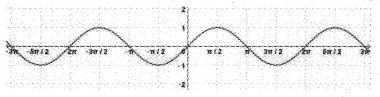
(i) Identify the function f (x)
(a) f(x) = sinx (b) f(x) = cos x
(c) f(x) = tanx (d) f(x) = cos ecx
(ii) Using the function f(x) find
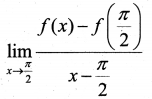
(i) (a) f(x) = sinx
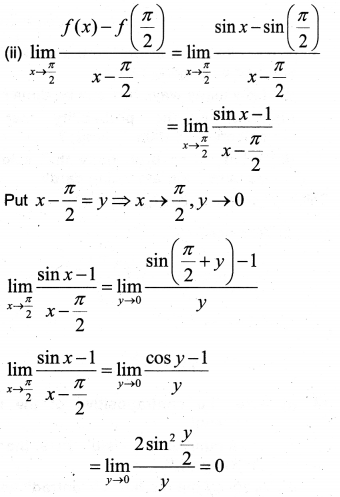
Question 7.
(i) Find the general term in the expansion of (x2+1x)5.
(ii) If the expansion of (x2+1x)n has a term independent of x, then which of the following can be the value of n?
(a) 18 (b) 16 (c) 22 (d) 13
Answer:
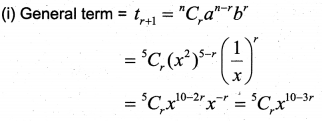
(ii) For getting a term independent of x in the expression of (x2+1x)n, power of x
2n – 3r = 0 ⇒ n = 3r2
Which means n should be a multiple 3 and divisible by 2. Hence (a) 18.
Answer any 8 from questions 8 to 17. Each question carries 4 scores. (8 × 4 = 32)
Question 8.
In a school, a survey among 400students, 100 were listed as taking apple juice, 150 as taking orange juice and 75 were listed as taking both apple juice as well as orange juice.
(i) How many students take apple juice or orange juice?
(ii) How many take apple juice alone but not orange juice?
(iii) How many students were taking neither apple juice nor orange juice?
Answer:
Let A: Apple juice, O: Orange juice.
(i) n(A ∪ O) = n(A) + n(O) – n(A ∩ O)
= 100 + 150 – 75 = 175
(ii) n(A ∩ O’) = n(A) – n(A ∩ O)
= 100 – 75 = 25
(iii) n(A’ ∩ O’) = 400 – n(A ∪ O)
= 400 – 175 = 225
Question 9.
The figure shows the graph of the function f(x).
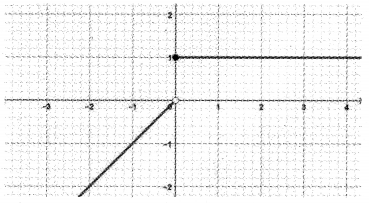
(i) Write the domain and range of f(x).
(ii) Find f(0)and f(-0.01).
(iii) Check the existence of limx→0 f(x).
Answer:
(i) Domain = R
Range = (-∞, 0) ∪ {1}
(ii) f(0) = 1, f(-0.01) = -0.01
(iii) limx→0− f(x) = 0, limx→0+ f(x) = 1
limx→0− f(x) = limx→0+ f(x)
Therefore limit does not exists.
OR
There is a break in the graph of f(x) at x = 0.
So limit does not exist at x = 0.
Question 10.
Consider the set A = {-1, 1}
(i) Write all elements is A × A.
(ii) How many relations are there from A to A?
(iii) Write all functions from A to A which has Range = {-1, 1}.
Answer:
(i) A × A = {(-1, -1), (-1, 1), (1, -1), (1, 1)}
(ii) Number of relations = 2n(A × A) = 24 =16
(iii) There are two functions
f1 ={(-1, -1), (1, 1)}
f2 = {(-1, 1), (1, -1)}
Question 11.
Using principle of mathematical induction prove that n(n +1)(n + 5) is a multiple of 3 for all n ∈ N.
Answer:
p(1) : 1(1 + 1)(1 + 5) = 12 divisible by 3, hence true. Assuming that true for p(k)
p(k) : k(k + 1 )(k + 5) is divisible by 3.
k(k + 1)(k + 5) = 3M
p(k + 1) : (k + 1)(k + 2)(k + 6)
= (k + 1)(k2 + 8k + 12)
= (k + 1)(k2 + 5k + 3k + 12)
= (k + 1) [k(k + 5) + 3(k + 6)]
= [k(k + 1)(k + 5) + 3(k +1)(k + 6)]
= [3M + 3(k + 1)(k + 6)]
= 3[M + (k + 1)(k + 6)]
Hence divisible by 3. Therefore by using the principle of mathematical induction true for all n ∈ N.
Question 12.
If z is a complex number with |z| = 2 and arg(z) = 4π3, then
(i) express z in a + ib form.
(ii) Find ˉz
(iii) Verify that (ˉz)2 = 2z
Answer:
(i) z = r(cosθ + i sinθ)
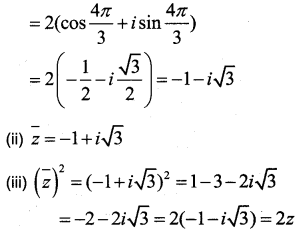
Question 13.
Seven cards are drawn from a pack of well shuffled 52 playing cards.
(i) How many ways this can be done?
(ii) What is the probability that the selection contain all kings?
(iii) What is the probability that selection does not contain a king card?
Answer:

Question 14.
(i) Write the contrapositive of the given statement.
“If a number is divisible by 9, then it is divisible by 3.”
(ii) Verify by the method of contradiction:
“p : √7 is irrational.”
Answer:
(i) If a number is not divisible by 3, it is not divisible by 9.
(ii) Assume that √7 is rational. Then √7 can be written in the form √7 = pq, where p and q are integers without common factors.
Squaring; 7 = p2q2 ⇒ 7q2 = p2
⇒ 7 divides p2 ⇒ 7 divides p
Therefore, p = 7k for some integer k.
=> p2 = 49k2 ⇒ 7q2 = 49k2 ⇒ q2 = 7k2
⇒ 7 divides q2 ⇒ 7 divides q
Hence p and q have common factor 7, which contradicts our assumption. Therefore, √7 is irrational.
Question 15.
Calculate the mean deviation about median for the following data:
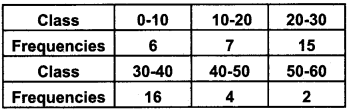
Answer:
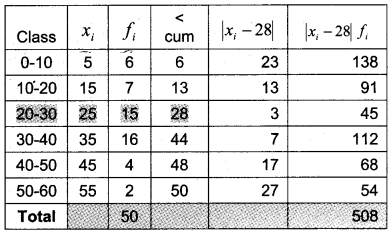
Median class is the class in which the (502=25)th
observation lies. Therefore median class is 20 – 30.

Question 16.
Consider the word ASSASSINATION
(i) How many different ways can the letters of the word are arranged
(ii) How many of these words have all vowels together?
Answer:
(i) In the word ASSASSINATION there are 13 letters, of which A appears 3 times, S appears 4 times, N appears 2 times, I appears 2 times and the rest all are different.
Therefore the total number of ways is

Question 17.
Let A (0, 7, 10), B(-1, 6, 6,) and C (-4, 9, 6) are the vertices of a triangle.
(i) Show that is a right triangle.
(ii) Find the coordinate of the centre of the circle passing through the point A, B, C.
Answer:
(i) AB2 = (-1 – 0)2 + (6 – 7)2 + (6 – 10)2
= 1 + 1 + 16 = 18
BC2 = (-4 – (-1))2 + (9 – 6)2 + (6 – 6)2
= 9 + 9 + 0 = 18
AC2 =(-4 – 0)2 + (9 – 7)2 + (6 – 10)2
= 16 + 4 + 16 = 36
AB2 + BC2 = AC2
Therefore triangle ABC is right triangle.
(ii) Since the triangle is a right triangle, the circumcentre will lie on the midpoint of the side AC.
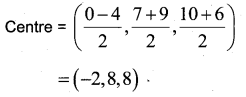
Answer any 5 from questions 18 to 24. Each question carries 6 score. (5 × 6 = 30)
Question 18.
The figure shows a unit circle and a line L which makes 30° with the positive direction of x – axis.
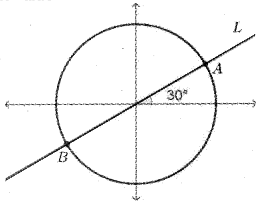
(i) Write the equation of the line L.
(ii) Write the coordinate of the points A and B.
(iii) Find the equation of the tangent line to the circle at A.
Answer:
i) The slope of the line L

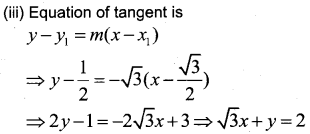
Question 19.
Consider two lines L1: 2x + y = 4 and L2: (2x – y = 2)
(i) Find the angle between L1 and L2.
(ii) Find the equation of the line passing through the intersection of L1 and L2
which makes an angle 45° with the positive direction of x – axis.
(iii) Find the x and y Intercepts of the third line obtained in part (ii).
Answer:
(i) The slope of the line L1 is -2.
The slope of the line L2 is 2.
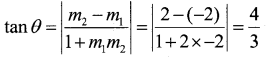
(ii) The family of lines is of the form
L1 + λL2 = 0
⇒ (2x + y – 4) + λ(2x – y – 2) = 0
⇒ (2 + 2λ)x + (1 – λ)y – 4 – 2λ = 0
⇒ Slope = −2+2λ1−λ = tan 45 = 1
⇒ -2 – 2λ = 1 – λ ⇒ λ = — 3
Equation of the line is 2x – 2y = 1

Question 20.
If an ellipse passing through (3, 1) having foci (±4, 0), then
(i) find the length of the major axis
(ii) find the standard equation of the ellipse.
(iii) find the eccentricity and length of the latus rectum.
Answer:
(i) Length of the major axis = Sum of the distances of the point (3, 1) from the foci (±4, 0)

Question 21.
(i) Find sin 75°
(ii) The figure shows ΔABC with side AC = 4√2 units inscribed in a circle of radius 4 units. The length of the arc BDC is 10π3 units.

(a) Write ∠A in degree measure.
(b) Find the length of the sides AB and BC.
Answer:
(i) sin(75°) = sin(45° + 30°)
= sin45° cos30° + cos45° sin30°
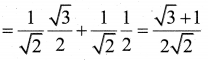
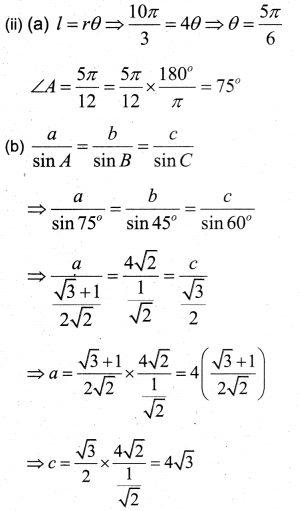
Question 22.
(i) Solve 3(x−2)5≤5(2−x)3
(ii) Solve the inequalities
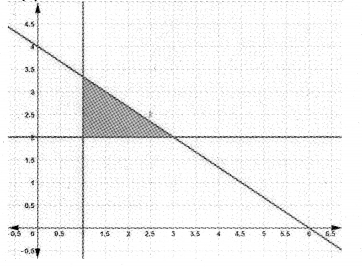
2x + 3y ≤ 12; x ≥ 1; y ≥ 2 graphically.
Answer:
(i) 3(x−2)5≤5(2−x)3
⇒ 9(x — 2) ≤ 25(2 – x)
⇒ 9x -18 ≤ 50 – 25x
⇒ 34x ≤ 68 ⇒ x ≤ 2
(ii)
Question 23.
(i) Find the derivative of y = x2 using the first principle.
(ii) Find dydx if y = x1+tanx
Answer:
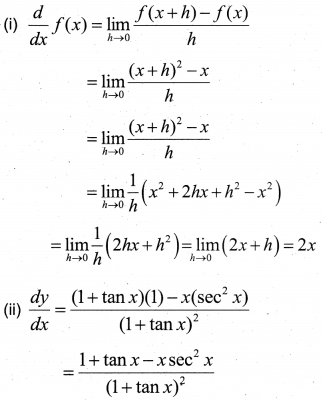
Question 24.
Consider the sequence 3, 6, 9, 12, ….., 99
(i) How many terms are there in the given sequence?
(ii) Find the mean of the sequence.
(iii) Find the sum of squares of each terms of the given sequence.
(iv) Find the variance of the sequence.
Answer:
(i) 3 × 1, 3 × 2, 3 × 3,…….. 3 × 33
Hence there are 33 terms in the given sequence.