Plus One Maths Notes Chapter 11 Conic Sections is part of Plus One Maths Notes. Here we have given Kerala Plus One Maths Notes Chapter 11 Conic Sections .
| Board | SCERT, Kerala |
| Text Book | NCERT Based |
| Class | Plus One |
| Subject | Maths Notes |
| Chapter | Chapter 11 |
| Chapter Name | Conic Sections |
| Category | Plus One Kerala |
Kerala Plus One Maths Notes Chapter 11 Conic Sections
I. Circle
A circle is the set of all points in a plane that are equidistant from a fixed point in the plane. The fixed point is the centre and the fixed distance is the radius.
Equation of a circle with centre origin and radius r is x2 + y2 = r2.
Equation of a circle with centre (h, k) and radius r is (x – h)2 + (y – k)2 = r2.
General form of the equation of a circle is x2 + y2 + 2gx + 2fy + c = 0 with centre (-g, -f) and radius \(\sqrt{g^{2}+f^{2}-c}\).
II. Conic
A conic is the set of all points in a plane which moves so that the distance from a fixed point is in a constant ratio to its distance from a fixed-line. The fixed point is the focus and fixed line is directrix and the constant ratio is eccentricity, denoted by ‘e’.
III. Parabola (e = 1)
y2 = 4ax
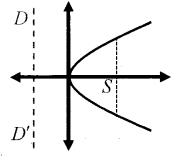
Vertex: (0, 0)
Focus(S): (a, 0)
Length of Latusrectum: (LL’) = 4a
Equation of directrix (DD’) is x = -a
y2 = -4ax
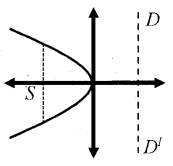
Vertex: (0, 0)
Focus(S): (-a, 0)
Length of Latusrectum (LL’) = 4a
Equation of directrix (DD’) is x = a
x2 = 4ay
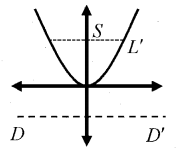
Vertex: (0, 0)
Focus(S): (0, a)
Length of Latusrectum (LL’) = 4a
Equation of directrix (DD’) is y = -a
x2 = -4ay
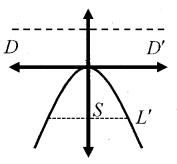
Vertex: (0, 0)
Focus(S): (0, -a)
Length of Latusrectum (LL’) = 4a
Equation of directrix (DD’) is y = a
IV. Ellipse (e < 1)
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\), a > b
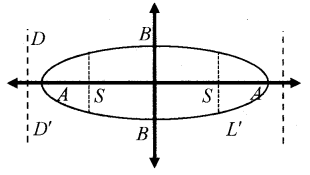
1. Eccentricity, e = \(\frac{\sqrt{a^{2}-b^{2}}}{a}\)
(ae)2 = a2 – b2 ⇒ c2 = a2 – b2
2. b2 = a2(1 – e2)
3. Length of Latusrectum (LL’) = \(\frac{2 b^{2}}{a}\)
4. Focii, S(ae, 0) and S'(-ae, 0) or S(c, 0), S'(-c, 0)
5. Centre (0, 0)
6. Vertices A(a, 0) and A'(-a, 0)
7. Equation of directrix (DD’) is x = \(\frac{a}{e}\) and x = \(-\frac{a}{e}\)
8. Length of major axis (AA’) = 2a
9. Length of minor axis'(BB’) = 2b
\(\frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}=1\), a > b
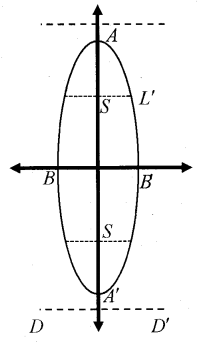
1. Eccentricity, e = \(\frac{\sqrt{a^{2}-b^{2}}}{a}\)
(ae)2 = a2 – b2 ⇒ c2 = a2 – b2
2. b2 = a2(1 – e2)
3. Length of Latus rectum (LL’) = \(\frac{2 b^{2}}{a}\)
4. Focii, S(0, ae) and S'(0, -ae) or S(0, c), S'(0, -c)
5. Centre (0, 0)
6. Vertices A(0, a) and A'(0, -a)
7. Equation of directrix (DD’) is y = \(\frac{a}{e}\) and y = \(-\frac{a}{e}\)
8. Length of major axis (AA’) = 2a
9. Length of minor axis (BB’) = 2b
V. Hyperbola (e > 1)
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)
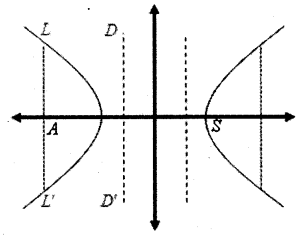
1. Eccentricity, e = \(\frac{\sqrt{a^{2}+b^{2}}}{a}\)
(ae)2 = a2 + b2 ⇒ c2 = a2 + b2
2. b2 = a2(e2 – 1)
3. Length of Latus rectum (LL’) = \(\frac{2 b^{2}}{a}\)
4. Focii, S(ae, 0) and S'(-ae, 0) or S(c, 0), S'(-c, 0)
5. Centre (0, 0)
6. Vertices A(a, 0) and A'(-a, 0)
7. Equation of directrix (DD’) is x = \(\frac{a}{e}\) and x = \(-\frac{a}{e}\)
\(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\)
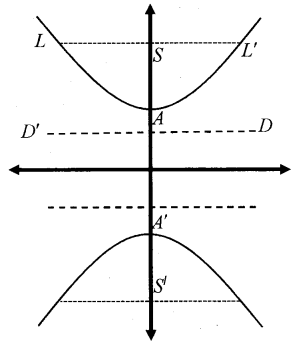
1. Eccentricity, e = \(\frac{\sqrt{a^{2}+b^{2}}}{a}\)
(ae)2 = a2 + b2 ⇒ c2 = a2 + b2
2. b2 = a2(e2 – 1)
3. Length of Latus rectum (LL’) = \(\frac{2 b^{2}}{a}\)
4. Focii, S(0, ae) and S'(0, -ae) or S(0, c), S'(0, -c)
5. Centre (0, 0)
6. Vertices A(0, a) anti A'(0, -a)
7. Equation of directrix (DD’) is y = \(\frac{a}{e}\) and y = \(-\frac{a}{e}\)
We hope the Plus One Maths Notes Chapter 11 Conic Sections help you. If you have any query regarding Kerala Plus One Maths Notes Chapter 11 Conic Sections, drop a comment below and we will get back to you at the earliest.