Plus One Maths Chapter Wise Questions and Answers Chapter 8 Binomial Theorem

Kerala Plus One Maths Chapter Wise Questions and Answers Chapter 8 Binomial Theorem

Plus One Maths Binomial Theorem Three Mark Questions and Answers

Question 1.
Write the middle term in the expansion of the following; (3 score each)

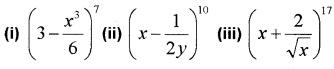
Answer:
i) Here 7 is an odd number. Therefore there are two middle terms \(\left(\frac{7+1}{2}=4\right)^{t h}\) and \(\left(\frac{7+1}{2}+1=5\right)^{t h}\), ie; 4^th and 5^th terms in the above expansion.

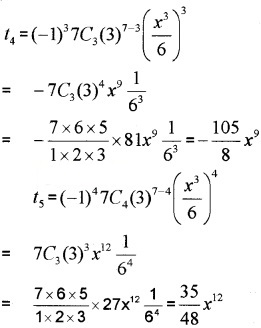
ii) Here 10 is an even number. Therefore middle terms \(\left(\frac{10}{2}+1=6\right)^{t h}\) term in the above expansion.

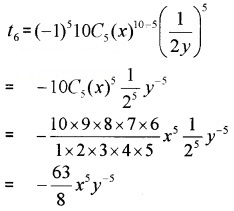
iii) Here 17 is an odd number. Therefore there are two middle terms \(\left(\frac{17+1}{2}=9\right)^{t h}\), ie; 9^th and 10^th terms in the above expansion. \(\left(x+\frac{2}{\sqrt{x}}\right)^{17}\).

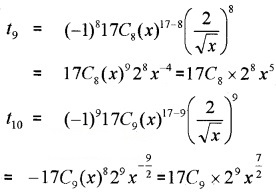
Question 2.
Find the term independent of x in the following expansion. (3 score each)

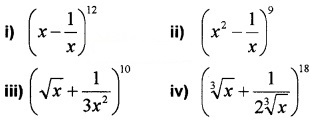
Answer:
i) General term = t_r+1 = (-1)^r12C_r(x)^12-r \(\left(\frac{1}{x}\right)^{r}\)
=(-1)^r12C_r(x)^12-r-r = (-1)^r12C_r(x)^12-2r
Term independent of x in the expansion will be the term in which the power of x is zero, ie; 12 – 2r = 0 ⇒ 12 = 2r
⇒ r = 6
t₇ = (-1)⁶12C⁶x^12-2(6)
= \(\frac{12 \times 11 \times 10 \times 9 \times 8 \times 7}{1 \times 2 \times 3 \times 4 \times 5 \times 6}\) = 924.

ii) General term = t_r+1 =(-1)^r9C_r(x²)^9-r\(\left(\frac{1}{x}\right)^{r}\)
= (-1)^r9C_r(x)^18-2r-r = (-1)^r9C_r(x)^18-3r
Term independent of x in the expansion will be the term in which the power of x is zero.
ie; 18 – 3r = 0 ⇒ 18 = 3r ⇒ r = 6
t₇ = (-1)⁶9C₆x^18-3(6)
= \(\frac{9 \times 8 \times 7}{1 \times 2 \times 3}\) = 84.

iii) General term = t_r+1

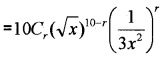
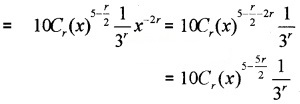
Term independent of x in the expansion will be the term in which the power of x is zero.

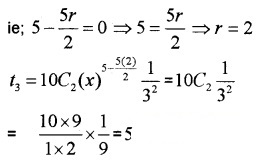
iv) General term = t_r+1

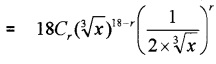
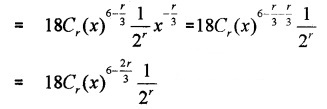
Term independent of x in the expansion will be the term in which the power of x is zero.

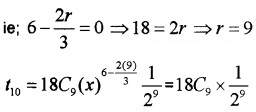
Question 3.
Find the coefficient of x¹⁰ in the expansion of \(\left(2 x^{2}-\frac{3}{x}\right)^{11}\).
Answer:
General term = t_r+1

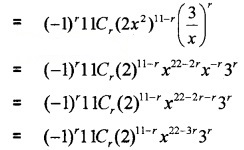
Given; 22 – 3r = 10 ⇒ 12 = 3r ⇒ r = 4
t₅ = (-1)⁴11C₄2^11-4 x^22-3(4) 3⁴
= 11C₄2⁷3⁴x¹⁰
Therefore the coefficient of x¹⁰ is 11C₄2⁷3⁴.

Question 4.
Find the coefficient of a⁵b⁷ in the expansion of (a – 2b)¹².
Answer:
General term = t_r+1 = (-1)^r12C_r(a)^12-r(2b)^r
= (-1)^r12C_r(a)^12-r2^rb^r
The term containing a⁵b⁷ is obtained by putting r = 7
⇒ t₈ = (-1)⁷12C₇(a)^12-72⁷b⁷
Therefore the coefficient of a⁵b⁷ is
(-1)⁷12C₇2⁷ = -12C₇2⁷.

Question 5.
Find the coefficient of (3 score each)

1. x¹¹ in the expansion of \(\left(x-\frac{2}{x^{2}}\right)^{17}\)
2. x⁹ in the expansion of \(\left(3 x^{2}+\frac{5}{x^{3}}\right)^{12}\)
3. x²⁰ in the expansion of \(\left(3 x^{3}-\frac{2}{x^{2}}\right)^{40}\)

Answer:
1. General term

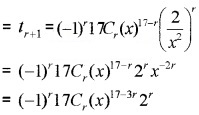
The term containing x¹¹ is obtained by
17 – 3r = 11 ⇒ 6 = 3r ⇒ r = 2
⇒ t₃ = (-1)²17C₂ (x)^17-3(2) 2² = 17C₂(x)¹¹ × 4
Therefore the coefficient of x¹¹ is 17C₂ × 4
= \(\frac{17 \times 16}{1 \times 2}\) × 4 = 544

2. General term

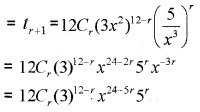
The term containing x⁹ is obtained by
24 – 5r = 9 ⇒ 15 = 5r ⇒ r = 3
⇒ t₄ = 12C₃(3)^12-3(x)^24-5(3)5³
= 12C₃(3)⁹(x)⁹5³
Therefore the coefficient of x⁹ is 12C₃(3)⁹5³.

3. General term = t_r+1
= (-1)^r40C_r(3x³)^40-r (\(\frac{2}{x^{2}}\))^r
= (-1)^r40C_r(3)^40-rx^120-3r (2)^r x^-2r
= (-1)^r40C_r(3)^40-rx^120-5r(2)^r
The term containing x²⁰ is obtained by
120 – 5r = 20 ⇒ 100 = 5r ⇒ r = 20
⇒ t₂₁ = (-1)²⁰40C₂₀(3)^40-20(x) ^120-5(20) 2²⁰
= 40C₂₀(3)²⁰(x)²⁰2²⁰
Therefore the coefficient of x²⁰ is 40C₂₀(3) ²⁰ 2²⁰.

Question 6.

1. Find the term independent of x in the expansion of \(\left(x^{2}+\frac{2}{x}\right)^{6}\) (3)
2. If the middle term in the expansion of \(\left(x^{m}+\frac{2}{x}\right)^{6}\) is independent of x, find the value of m.

Answer:
1. t_r+1 = ⁿC_ra^n-rb^r = ⁶C_r(x²)^6-r\(\left(\frac{2}{x}\right)^{r}\)
= ⁶C_rx^12-2rx^-r(2)^r = ⁶C_rx^12-3r(2)^r
For term independent of x;
12 – 3r = 0 r = 4
t₅ = ⁶C₄(2)⁴ = ⁶C₂ × 16 = \(\frac{6 \times 5}{1 \times 2}\) × 16 = 240

2. m = 1

Plus One Maths Binomial Theorem Four Mark Questions and Answers

Question 1.

1. Write the general term in the expansion \(\left(\frac{3 x^{2}}{2}-\frac{1}{3 x}\right)^{6}\) (2)
2. Find the term independent of x in the above expansion. (2)

Answer:
1. General term = t_r+1

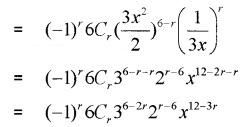
2. Term independent of x in the expansion will be the term in which the power of x is zero.
ie; 12 – 3r = 0 ⇒ 12 = 3r ⇒ r = 4

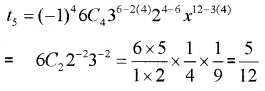
Plus One Maths Binomial Theorem Practice Problems Questions and Answers

Question 1.
Expand the following. (2 score each)

1. (3a² – 2b)⁴
2. (3 – 4x²)⁵
3. \(\left(\frac{x}{2}-2 y\right)^{6}\)
4. \(\left(\frac{x}{2}-2 y\right)^{6}\)

Answer:
1.

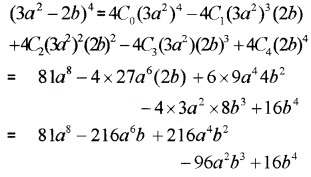
2.

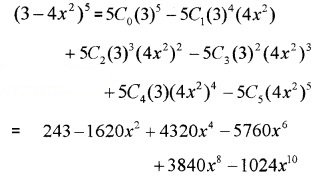
3.

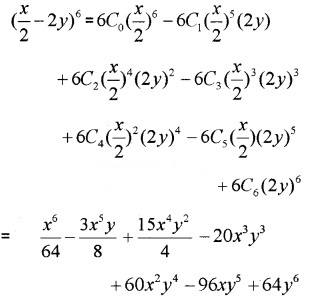
4.

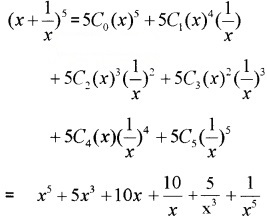
Question 2.
Write the general term in the expansion of the following; (2 score each)

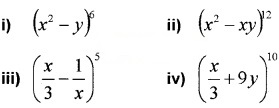
Answer:
i) General term = t_r+1
= (-1)^r6C_r(x²)^6-r(y)^r
= (-1)^r6C_rx^12-ry^r.

ii) General term = t_r+1

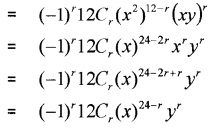
iii) General term = t_r+1

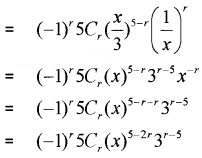
iv) General term = t_r+1

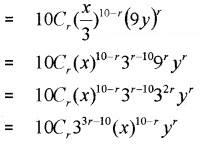
Question 3.
If the coefficient of x² in the expansion of (1 + x)ⁿ is 6 then the positive value of n.
Answer:
t_r+1 = nC_rx^r, the term containing x² is obtained by putting r= 2.
nC₂ = 6 ⇒ \(\frac{n(n-1)}{2}\) = 6 ⇒ n(n -1) = 12
⇒ n(n -1) = 4 × 3 ⇒ n = 3.

Question 4.
Find the 13^th term in the expansion of \(\left(9 x-\frac{1}{3 \sqrt{x}}\right)^{18}\).
Answer:

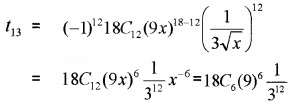
= 18C₆(3)^12-12 = 18C₆ = 18564

Plus One Maths Chapter Wise Questions and Answers