Kerala Plus One Maths Chapter Wise Questions and Answers Chapter 6 Linear Inequalities
Plus One Maths Linear Inequalities Three Mark Questions and Answers
Question 1.
Solve the following inequalities.
- 12(3x5+4)≥13(x−6)
- (2x−13)≥(3x−2)4−(2−x)5 (3 score each)
Answer:
1. Given;
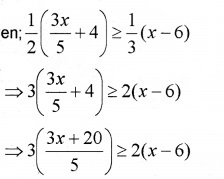
⇒ 3(3x + 20) ≥ 10(x – 6)
⇒ 9x + 60 ≥ 10x – 60
⇒ 9x – 10x ≥ -60 – 60
⇒ -x ≥ -120 ⇒ x ≤ 120
2. Given;
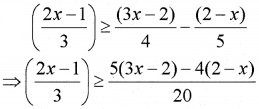
⇒ 20(2x -1) ≥ 3[15x – 10 – 8 + 4x]
⇒ 40x – 20 ≥ 45x – 54 + 12x
⇒ 40x – 20 ≥ 57x – 54
⇒ 40x – 57x ≥ -54 + 20
⇒ -17x ≥ -34 ⇒ x ≤ 2
Question 2.
1. Which of the following sets of inequality represent the second quadrant? (1)
(a) x < 0, y < 0
(b) x > 0, y > 0
(c) x < 0, y > 0
(d) x > 0, y < 0
2. Write the system of inequalities that represents the shaded rectangle in the figure given below: (2)
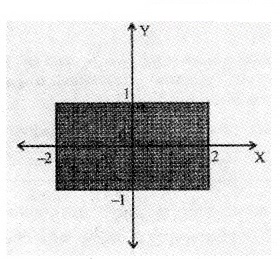
Answer:
1. (a) x < 0, y < 0
2. The shaded figure is a rectangle. The side parallel to x axis are y = -1 and y = 1. The side perpendicular to x axis are x = 2 and x = -2. Hence the inequality that represent the shaded region are
-2 ≤ x ≤ 2; -1 ≤ y ≤ 1.
Question 3.
Find all pairs of consecutive even positive integers both of which are smaller than10 such that their sum is less than 23.
Answer:
Consecutive even positive integers be x and x + 2. Then, x + x + 2 < 23; x + 2 < 10
⇒ 2x < 23 – 2; x < 10 – 2
⇒ x < 212 = 10.5; x < 8
⇒ 8 < x ≤ 10 Therefore x can take values 9, 10. Hence the pairs are (9, 10), (10, 9).
Question 4.
The longest side of a triangle is 3 times the shortest side and the third side is 2 cm shorter than the longest side. If the perimeter of the triangle is at least 61 cm, find the minimum length of the shortest side.
Answer:
Let the shortest side is x, then;
Longest side = 3x;
Third side = Longest side – 2 = 3x – 2
Perimeter = 3x + 3x – 2 + x ≥ 61 ⇒ 7x – 2 ≥ 61
⇒ 7x ≥ 61 + 2 ⇒ x ≥ 637 = 9.
Plus One Maths Linear Inequalities Four Mark Questions and Answers
Question 1.
Solve the following system of inequalities graphically.
- 2x – y > 1; x – 2y < -1
- x + y ≤ 9; y > x; x ≥ 0
- x – 2y ≤ 3; 3x + 4y ≥ 12; x ≥ 0, y ≥ 1
- 2x + y – 3 ≥ 0; x – 2y + 1 ≥ 0; y ≤ 3 (4 score each)
Answer:
1. 2x – y > 1; x – 2y < -1

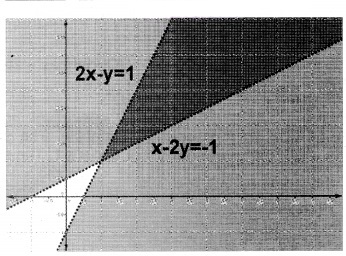
2. x + y ≤ 9; y > x ⇒ x – y < 0

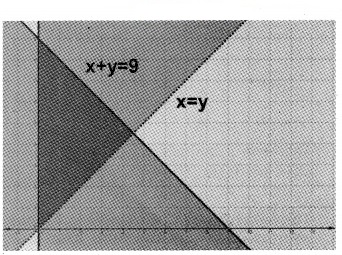
3. x – 2y ≤ 3; 3x + 4y ≥ 12

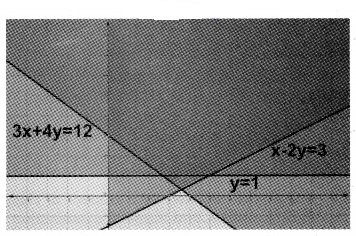
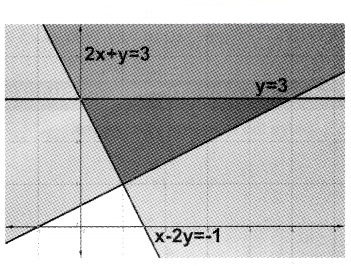
4. 2x + y ≥ 3; x – 2y ≤ -1

Plus One Maths Linear Inequalities Practice Problems Questions and Answers
Question 1.
Solve the following inequalities.
- 4x + 3 < 5x + 7
- 3(x – 1) ≤ 2(x – 3) (1 score each)
Answer:
1. Given; 4x + 3 < 5x + 7
⇒ 4x – 5x < 7 – 3 ⇒ -x < 4 ⇒ x > -4.
2. Given; 3(x – 1) < 2(x – 3)
⇒ 3x – 3 ≤ 2x – 6 ⇒ 3x – 2x ≤ -6 + 3
⇒ x ≤ -3.
Question 2.
Solve the inequality 3(x−2)5≤5(2−x)3.
Answer:
Given; 3(x−2)5≤5(2−x)3
⇒ 9(x – 2) ≤ 25(2 – x)
⇒ 9x – 18 ≤ 50 – 25x
⇒ 9x + 25x ≤ 50 + 18
⇒ 34x ≤ 68 ⇒ x ≤ 2.
Question 3.
Show the solution of each inequality on a number line.
- 4x + 3 < 6x + 7
- 5x – 3 ≥ 3x – 5
- 3(1 – x) < 2(x + 4)
- 2 – 3x < 2(x + 6)
- -3 ≤ 3 – 2x < 6 (2 score each)
Answer:
1. Given; 4x + 3 < 6x + 7 ⇒ 4x – 6x < 7 – 3
⇒ -2x < 4 ⇒ x > -2
![]()
2. Given; 5x – 3 > 3x – 5 ⇒ 5x – 3x ≥ -5 + 3
⇒ 2x ≥ -2 ⇒ x ≥ 1.
![]()
3. Given; 3(1 – x) < 2(x + 4) ⇒ 3 – 3x < 2x + 8
⇒ -3x – 2x < 8 – 3 ⇒ -5x < 5 ⇒ x > -1.
![]()
4. Given; 2 – 3x < 2(x + 6) ⇒ 2 – 3x < 2x + 12
⇒ -3x – 2x < 12 – 2 ⇒ -5x < 10 ⇒ x > -2
![]()
5. Given; -3 ≤ 3 – 2x < 6
⇒ -3 ≤ 3 – 2x; 3 – 2x < 6
⇒ -3 – 3 ≤ -2x; -2x < 6 – 3
⇒ -6 ≤ -2x; -2x < 3 ⇒ 3 ≥ x; x > −32 ⇒ −32 < x ≤ 3
![]()
Question 4.
The marks obtained by a student of class XI in first and second terminal examination are 62 and 48, respectively. Find the minimum marks he should get in the annual examination to have an average of at least 60 marks.
Answer:
Let x denote the mark obtained by the student in Class XI examination, then;
62+48+x3 ≥ 60 ⇒ 110 + x ≥ 1800 ⇒ x ≥ 70.
