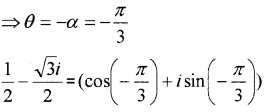Plus One Maths Chapter Wise Questions and Answers Chapter 5 Complex Numbers and Quadratic Equations

Kerala Plus One Maths Chapter Wise Questions and Answers Chapter 5 Complex Numbers and Quadratic Equations

Plus One Maths Complex Numbers and Quadratic Equations Three Mark Questions and Answers

Question 1.
If z₁ = 2 – i, z₂ = 1 + i

1. Find | z₁ + z₂ + 1| and |z₁ – z₂ + i| (2)
2. Hence find $\left|\frac{z_{1}+z_{2}+1}{z_{1}-z_{2}+i}\right|$ (1)

Answer:
1. |z₁ + z₂ + 1| = |2 – i + 1 + i + 1| = 4
|z₁ – z₂ + i| = |2 – i – 1 – i + i| = |1 – i|
$=\sqrt{1+1}=\sqrt{2}$

2.

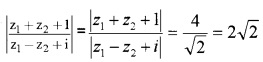
Question 2.
Find the square root of -15 – 8i.
Answer:
Let x + iy = $\sqrt{-15-8 i}$
Then (x + iy)² = -15 – 8i
⇒ x² – y² + 2xyi = – 15 – 8i
Equating real and imaginary parts, we have
x² – y² = -15 ______(1)
2xy = – 8
We know the identity
(x² + y²)² = (x² – y²)² + (2xy)²
= 225 + 64
= 289
Thus, x² + y² = 17 _______(2)
From (1) and (2), x² = 1 and y² = 16 or x = ±1 and y = ±4
Since the product xy is negative, we have
x = 1, y = -4 or, x = -1, y = 4
Thus, the square roots of -15 – 8i are 1 – 4i and -1 + 4i.

Plus One Maths Complex Numbers and Quadratic Equations Four Mark Questions and Answers

Question 1.
Consider the complex number $\frac{i-1}{\cos \frac{\pi}{3}+i \sin \frac{\pi}{3}}$

1. Express in a + ib form. (2)
2. Convert into polar form. (2)

Answer:
1.

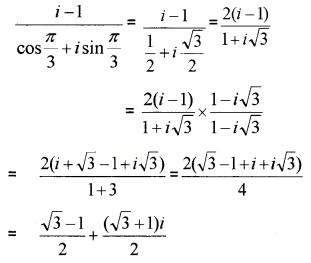
2.

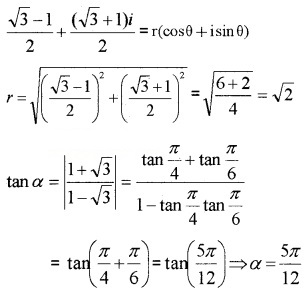
The complex number lies in the first quadrant;
⇒ θ = α = $\frac{5 \pi}{12}$

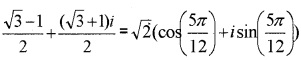
Question 2.

1. Express the complex number $\frac{2-i}{(1-i)(1+2 i)}$ in the form a + ib (2)
2. Solve the equation 27x² – 10x + 1 = 0 (2)

Answer:
1.

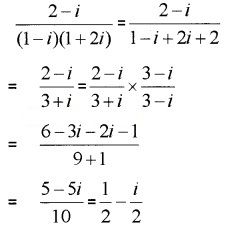
2. 27x² – 10x + 1 = 0

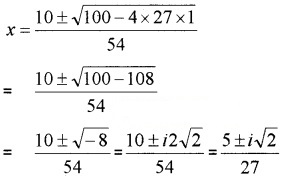
Question 3.

1. For what value of x and y 4x + i(3x – y) = 3 – 6i (2)
2. Solve the equation 21x² – 28x + 10 = 0 (2)

Answer:
1. Given; 4x + i(3x – y) = 3 – 6i
⇒ 4x = 3; 3x – y = -6

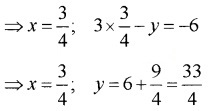
2. 21x² – 28x + 10 = 0

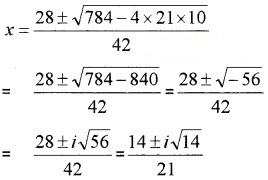
Question 4.
Consider the complex number z = $\frac{1+i}{1-i}$
1. Write z in a + ib form.
2.

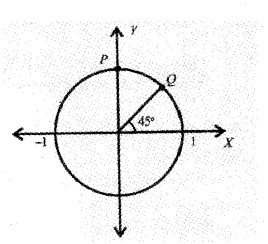
In the figure radius of the circle is 1. Write the polar form of the complex number represent by the points P and Q. (2)
3. Find the square root of i. (2)
Answer:
1.

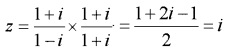
2. Polar form of the point P is $1\left(\cos \frac{\pi}{2}+i \sin \frac{\pi}{2}\right)$
Polar form of the point Q is $1\left(\cos \frac{\pi}{4}+i \sin \frac{\pi}{4}\right)$

3. i = 0 + i ⇒ $\sqrt{i}$ = x + iy ⇒ i = x² + y² + 2xyi x² + y² = 0; 2xy = 1
(x² + y²)² = (x² – y²)² + 4x²y²
(x² + y²)² = 0 + (1)² = 1
x² + y² = 1; x² + y² = 0

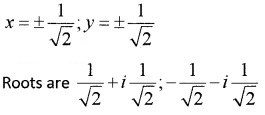
Plus One Maths Complex Numbers and Quadratic Equations Six Mark Questions and Answers

Question 1.

1. Express the complex number $\frac{3-\sqrt{-16}}{1-\sqrt{-9}}$ in the form a + ib (2)
2. Represent the complex number $\frac{5+i \sqrt{3}}{-4+2 \sqrt{3 i}}$ in the polar form. (2)
3. Solve the equation ix² – x + 12i = 0 (2)

Answer:
1.

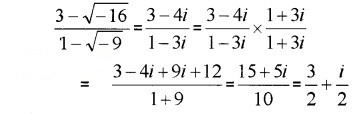
2.

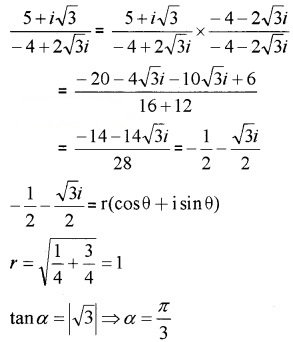
The complex number lies in the third quadrant;

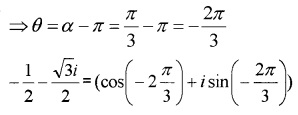
3. ix² – x + 12i = 0

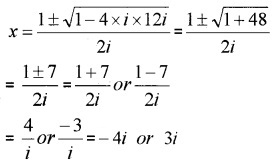
Plus One Maths Complex Numbers and Quadratic Equations Practice Problems Questions and Answers

Question 1.
Express each of the following in a + ib form. (1 score each)

1. (2 – 4i) + (5 + 3i)
2. (1 – i) – (-1 + 6i)
3. 3(7 + 7i) + i(7 + 7i)
4. $\left(\frac{1}{5}+i \frac{2}{5}\right)-\left(4+\frac{5}{2} i\right)$

Answer:
1. (2 – 4i) + (5 + 3i) = (2 + 5) + (-4 + 3)i = 7 – i

2. (1 – i) – (-1 + 6i) = 1 – i + 1 – 6i = 2 – 7i

3. 3(7 + 7i) + i(7 + 7i) = 21 + 21i + 7i – 7 = 14 + 28i

4.

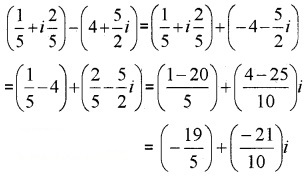
Question 2.
Express each of the following in a + ib form. (1 score each)

1. (-5i)($\frac{1}{8}$i)
2. (-i)(2i)(-$\frac{1}{8}$i)³
3. i⁹⁹
4. i¹¹¹ + i²²² + i³³³
5. (7 – i)(2 + 7i)
6. (-1 – i)(4 + 2i)
7. (5 – 3i)²
8. ($\frac{1}{3}$ + 3i)³

Answer:
1.

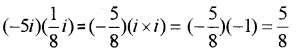
2.

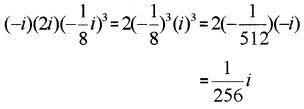
3. i⁹⁹ = i^{96 + 3} = i⁹⁶i³ = -i

4. i¹¹¹ + i²²² + i³³³ + i¹⁰⁸ + i^{220 + 2} + i^{332 + 1}
= i³ + i² + i¹ = -i – 1 + i = -1

5. (7 – i)(2 + 7i) = 7 × 2 – 2i + 7 × 7i – i × 7i
= 14 – 2i + 49i + 7 = 21 + 47i

6. (-1 – i)(4 + 2i) = -4 – 4i – 2i + 2 = – 2 – 6i

7. (5 – 3i)² = 5² – 2 × 5 × 3i + (3i)²
= 25 – 30i – 9 = 16 – 30i

8.

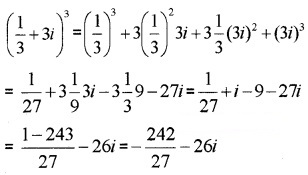
Question 3.
Find the multiplicative inverse of the following; (1 score each)

1. 3 – 4i
2. 2 – 3i
3. $\sqrt{5}$ + 3i

Answer:
1. Multiplicative inverse = $\frac{1}{3-4 i}$

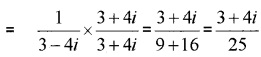
2. Multiplicative inverse = $\frac{1}{2-3 i}$

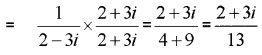
3. Multiplicative inverse = $\frac{1}{\sqrt{5}+3 i}$

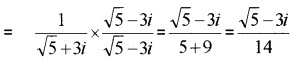
Question 4.
Express each of the following in a + ib form. (2 score each)

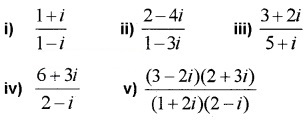
Answer:

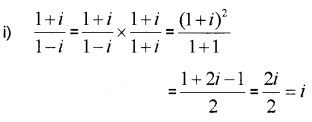
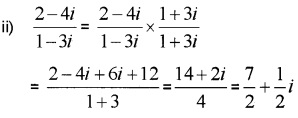
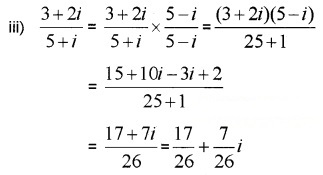
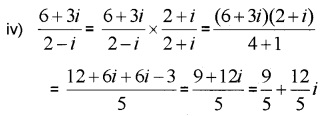
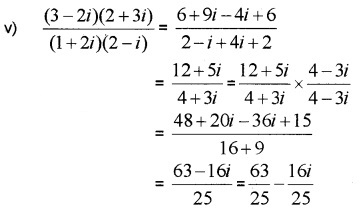
Question 5.
Convert the following into polar form. (2 score each)

1. 1 + i
2. -1 + i
3. $\sqrt{3}$ – i
4. $\frac{5-\sqrt{3} i}{4+2 \sqrt{3} i}$

Answer:
1. Given; 1 + i = r(cosθ + isinθ)
r = $\sqrt{1+1}=\sqrt{2}$
tanα = $\left|\frac{1}{1}\right|$ = 1 ⇒ α = $\frac{\pi}{4}$
The complex number lies in the first quadrant;

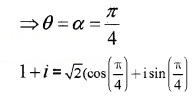
2. -1 + i = r(cosθ + isinθ)
r = $\sqrt{1+1}=\sqrt{2}$
tanα = $\left|\frac{1}{-1}\right|$ = 1 ⇒ α = $\frac{\pi}{4}$
The complex number lies in the second quadrant;

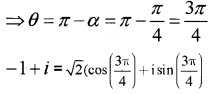
3.

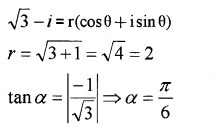
The complex number lies in the fourth quadrant;

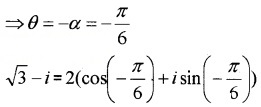
4.

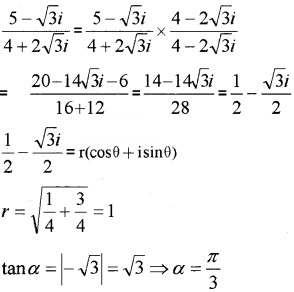
The complex number lies in the fourth quadrant;

Plus One Maths Chapter Wise Questions and Answers