Plus One Maths Chapter Wise Questions and Answers Chapter 4 Principle of Mathematical Induction

Kerala Plus One Maths Chapter Wise Questions and Answers Chapter 4 Principle of Mathematical Induction

Plus One Maths Principle of Mathematical Induction Three Mark Questions and Answers

Question 1.
For all n ≥ 1, prove that
1² + 2² + 3² +……….+ n² > \(\frac{n^{3}}{3}\)
Answer:
Let p(n): 1² + 2² + 3² + n²
Put n = 1 ⇒ p(1) = 1 > \(\frac{1}{3}\) which is true.
Assuming that true for p(k)
p(k): 1² + 2² + 3² +……….+ k² > \(\frac{k^{3}}{3}\)
Let p(k + 1): 1² + 2² + 3² +…….+ k² + (k + 1)² > \(\frac{k^{3}}{3}\) + (k + 1)²


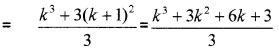
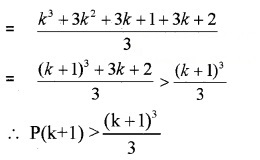
Hence by using the principle of mathematical induction true for all n ∈ N.

Question 2.
For all n ≥ 1 , prove that 1 + 2 + 3 +…….+ n < \(\frac{1}{8}\)(2n + 1)²
Answer:
Let p(n): 1 + 2 + 3 +…….+ n ,
Put n = 1 ⇒ p(1) = 1 < \(\frac{9}{8}\) which is true.
Assuming that true for p(k)
p(k): 1 + 2 + 3 +…….+ k < \(\frac{1}{8}\)(2k + 1)²
Let p(k +1): 1 + 2 + 3 +……..+ k + (k +1) < \(\frac{1}{8}\) (2k + 1)² + (k + 1)

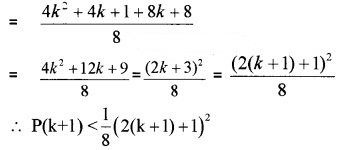
Hence by using the principle of mathematical induction true for all n ∈ N.

Question 3.
For all n ≥ 1, prove that p(n): 2³ⁿ – 1 is divisible by 7.
Answer:
p(1): 2³⁽¹⁾ – 1 = 8 – 1 = 7 divisible by 7, hence true. Assuming that for p(k)
p(k) : 2^3k – 1 is divisible by 7.
2^3k – 1 = 7M
P(k + 1): 2^{3(k + 1)} – 1 = 2^{3k + 3} – 1
= 2^3k2³ – 1 = 2^3k × 8 – 1
= 2^3k × 8 – 8 + 7 = 8(2^3k – 1) + 7
= 8(7M) + 7
Hence divisible by 7. Therefore by using the principle of mathematical induction true for all n ∈ N.

Question 4.
For all n ≥ 1, prove that p(n): n³ + (n + 1)³ + (n + 2)³ is divisible by 9.
Answer:
p(1): 1 + 2³ + 3³ = 1 + 8 + 27 = 36 divisible by 9, hence true. Assuming that true for p(k)
p(k): k³ + (k + 1)³ + (k + 2)³ is divisible by 9.
⇒ k³ + (k + 1)³ + (k + 2)³ = 9M
p(k +1 ): (k + 1)³ + (k + 2 )³ + (k + 3)³
= (k +1)³ + (k + 2)³ + k³ + 9k² + 27k + 27
= [(k + 1)³ + (k + 2)³ + k³] + 9[k² + 3k + 3]
= 9M + 9[k² + 3k + 3]
Hence p(k + 1)divisible by 9. Therefore by using the principle of mathematical induction true for all n ∈ N.

Plus One Maths Principle of Mathematical Induction Four Mark Questions and Answers

Question 1.
For all n ≥ 1, prove that

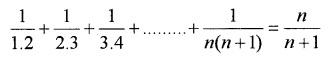
Answer:

Hence by using the principle of mathematical induction true for all n ∈ N.

Question 2.
For all n ≥ 1, prove that

Answer:
Let

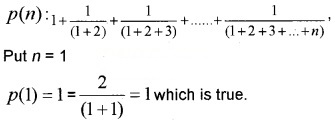
Assuming that true for p(k)

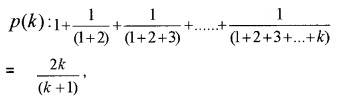
Let p(k + 1):

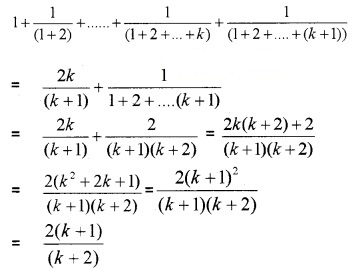
Hence by using the principle of mathematical induction true for all n ∈ N.

Question 3.
For all n ≥ 1 , prove that 1.2.3 + 2.3.4 +………+ n(n + 1)(n + 2) = \(\frac{n(n+1)(n+2)(n+3)}{4}\).
Answer:
Let p(n): 1.2.3 + 2.3.4 +……..+ n(n + 1)(n + 2),
Put n = 1
p(1) = \(\frac{1(1+1)(1+2)(1+3)}{4}\) = 6 which is true.
Assuming that true for p(k)
p(k): 1.2.3 + 2.3.4 +……..+ k(k + 1)(k + 2) = \(\frac{k(k+1)(k+2)(k+3)}{4}\),
Let p(k + 1)

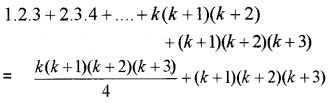
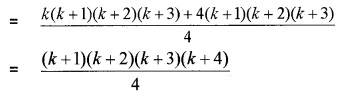
Hence by using the principle of mathematical induction true for all n ∈ N.

Question 4.
For all n ≥ 1, prove that

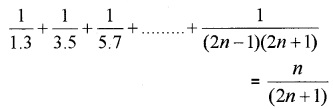
Answer:

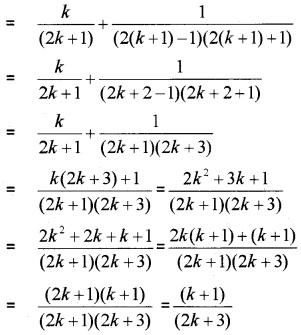
Hence by using the principle of mathematical induction true for all n ∈ N.

Question 5.
For all n ≥ 1 , prove that p(n): n(n + 1 )(n + 5) is divisible by 3.
Answer:
p(1): 1(1 + 1)(1 + 5) = 12divisible by 3, hence true. Assuming that true for p(k)
p(k): k(k + 1)(k + 5) is divisible by 3.
k(k + 1)(k + 5) = 3M
p(k + 1): (k + 1)(k + 2)(k + 6)
= (k + 1)(k² + 8k + 12)
= (k + 1)(k² + 5k + 3k +12)
= (k + 1)[k(k + 5) + 3(k + 6)]
= [k(k + 1)(k + 5) + 3(k + 1)(k + 6)]
= [3M + 3(k + 1)(k + 6)]
= 3[M + (k + 1)(k + 6)]
Hence divisible by 3. Therefore by using the principle of mathematical induction true for all n ∈ N.

Question 6.
For all n ≥ 1 , prove that p(n): 2.7ⁿ + 3.5ⁿ – 5 is divisible by 24.
Answer:
p(1): 2.7¹ + 3.5¹ – 5 = 14 + 15 – 5 = 24 divisible by 24, hence true. Assuming that true for p(k)
p(k): 2.7^k + 3.5^k – 5 is divisible by 24.
⇒ 2.7^k + 3.5^k – 5 = 24M
p(k + 1): 2.7^{k + 1} + 3.5^{k + 1} – 5
= 2.7^k.7 + 3.5^k.5 – 5
= 2.7^k.(6 + 1) + 3.5^k.(4 + 1) – 5
= 12.7^k + 2.7^k + 12.5^k + 3.5^k – 5
= 12(7^k + 5^k) + (2.7^k + 3.5^k) – 5
= 12(7^k + 5^k) + 24M
7^k And 5^k are odd numbers, therefore (7^k + 5^k) will be an even and will be divisible by 24, Hence p(k + 1)divisible by 24. Therefore by using the principle of mathematical induction true for all n ∈ N.

Plus One Maths Chapter Wise Questions and Answers