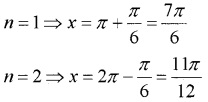Plus One Maths Chapter Wise Questions and Answers Chapter 3 Trigonometric Functions

Kerala Plus One Maths Chapter Wise Questions and Answers Chapter 3 Trigonometric Functions

Plus One Maths Trigonometric Functions Three Mark Questions and Answers

Question 1.
Prove the following

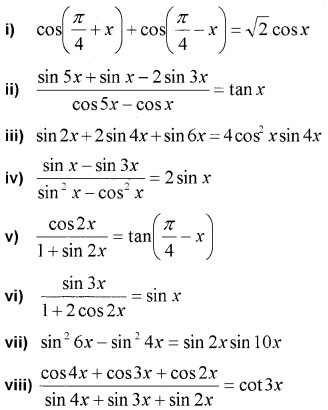
Answer:
i) LHS

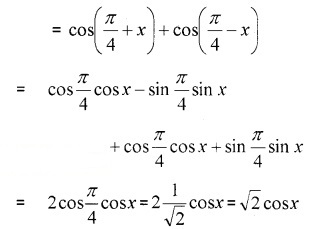
ii) LHS

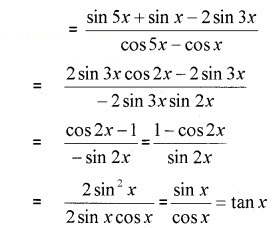
iii) LHS = sin 2x + 2 sin 4x + sin 6x
= 2 sin 4xcos2x + 2sin 4x
= 2 sin 4x(cos2x + 1) = 4 cos² x sin 4x

iv) LHS

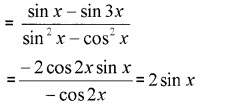
v) LHS

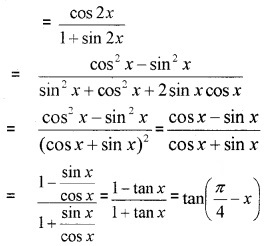
vi) LHS

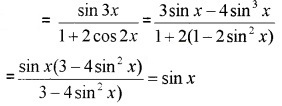
vii) LHS = sin² 6x – sin² 4x

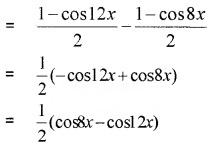
= 2 sin 10x sin(-2x)
= 2 sin 10x sin2x

viii) LHS

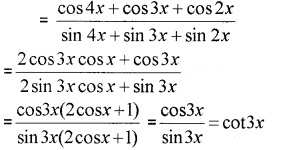
Question 2.
Find the general solution of the following equations.

1. cos4x = cos2x
2. sin 2x +cosx = 0
3. cos3x + cosx – cos2x = 0

Answer:
1. Given; cos 4x = cos 2x
⇒ cos4x – cos 2x = 0
⇒ -2 sin 3x sin x = 0
General solution is
⇒ sin3x = 0; ⇒ 3x = nπ ⇒ x = \(\frac{n \pi}{3}\), ∈ Z
Again we have;
⇒ sinx = 0; ⇒ x = nπ; n ∈ Z

2. Given; sin 2x + cosx = 0
⇒ 2sin xcosx + cosx = 0
⇒ cosx(2sin x + 1) = 0
General solution is
⇒ cosx = 0 ⇒ x = (2n + 1) \(\frac{\pi}{2}\), n ∈ Z
Again we have; 2sin x + 1 = 0

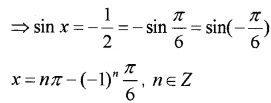
3. Given; cos3x +cosx – cos2x = 0
⇒ 2 cos2x cosx – cos2x = 0
⇒ cos2x(2cosx – 1) = 0
General solution is

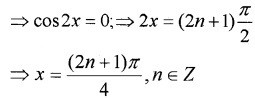
Again we have; 2cosx -1 = 0

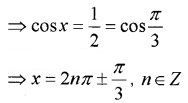
Question 3.
In Triangle ABC, if a = 25, b = 52 and c = 63, find cos A and sin A.
Answer:

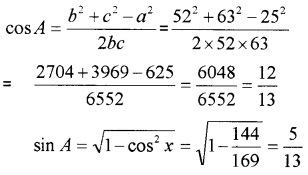
Question 4.
For any ΔABC, prove that a(b cosC – c cosB) = b² – c²
Answer:
LHS = ab cos C – ac cos B

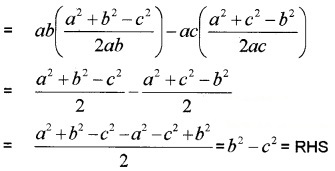
Question 5.
For any ΔABC, prove that, \(\frac{\sin (B-C)}{\sin (B+C)}=\frac{b^{2}-c^{2}}{a^{2}}\).
Answer:

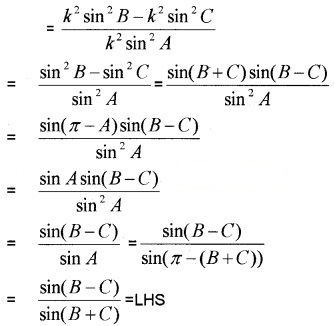
Question 6.

1. Convert \(\frac{2 \pi}{3}\) radian measure into degree measure. (1)
2. Prove that \(\frac{\sin 5 x+\sin 3 x}{\cos 5 x+\cos 3 x}=\tan 4 x\) (2)

Answer:
1. \(\frac{2 \pi}{3}=\frac{2 \pi}{3} \times \frac{180}{\pi}=120^{\circ}\)

2. LHS

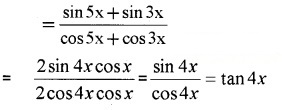
Plus One Maths Trigonometric Functions Four Mark Questions and Answers

Question 1.
For any ΔABC, prove that

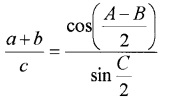
Answer:

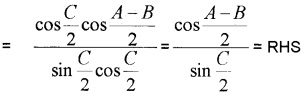
Question 2.
For any ΔABC, prove that \(\sin \frac{B-C}{2}=\frac{b-c}{a} \cos \frac{A}{2}\).
Answer:

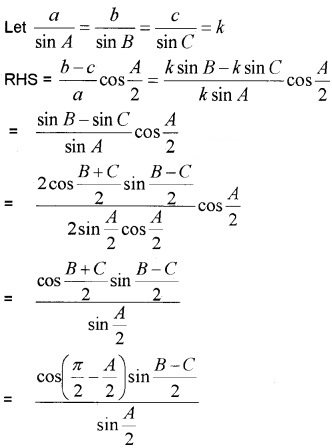
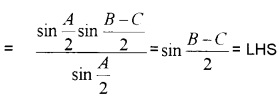
Question 3.
(i) Which of the following is not possible. (1)
(a) sin x = \(\frac{1}{2}\)
(b) cos x = \(\frac{2}{3}\)
(c) cosec x = \(\frac{1}{3}\)
(d) tan x = 8
(ii) Find the value of sin 15°. (2)
(iii) Hence write the value of cos 75° (1)
Answer:
(i) (c) cosec x = \(\frac{1}{3}\)

(ii) sin 15° = sin(45° – 30°)
= sin45°cos30°- cos45°sin30°

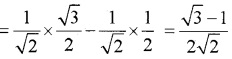
(iii) sin 15° = sin(90° – 75°) = cos 75°

Plus One Maths Trigonometric Functions Six Mark Questions and Answers

Question 1.
The angle of elevation of the top point P of the vertical tower PQ of height h from a point A is 45° and from a point B, the angle of elevation is 60°, where B is a point at a distance d from the point A measured along the line AB which makes angle 30° with AQ. Prove that d = h(\(\sqrt{3}\) – 1).
Answer:

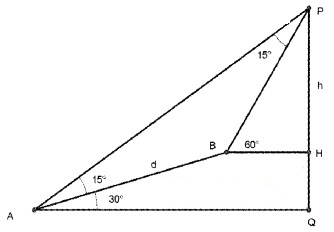
From the figure we have ∠PAQ = 45°, ∠BAQ = 30°and ∠PBH = 60°
in right ∆AQP
Clearly ∠APQ = 45°, ∠BPH = 30° , giving ∠APB = 15° ⇒ ∠PAB = 15°
In ∆APQ ,PQ = AQ = h
AP² = h² + h² = 2h² ⇒ AP = \(\sqrt{2}\)h
From ∆ABP,

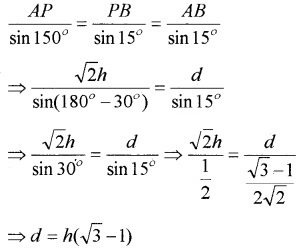
Question 2.
A tree stands vertically on a hillside which makes an angle of 15° with the horizontal. From a point on the ground 35m down the hill from the base of the tree, the angle of elevation of the top of the tree is 60°. Find the height of the tree.
Answer:

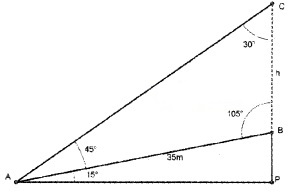
Let BC represent the tree, A be the point 35m down the hill from the base of the tree and h be the height of the tree.
Clearly in ∆ABC
∠BAC = 60°- 15° =45°;
∠ACB = 30°; ∠ABC = 105°

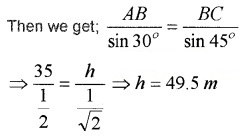
Question 3.
(i) If sin x = cos x, x ∈ [0, π] then is
(a) 0
(b) \(\frac{\pi}{4}\)
(c) \(\frac{\pi}{3}\)
(d) π
(ii) Write the following in ascending order of tits values, sin 100°, sin 0°, sin 50°, sin 200°
(iii) Solve: sin2x – sin4x + sin6x = 0
Answer:
(i) (b) \(\frac{\pi}{4}\)

(ii) sin 100° = sin(l 80 – 80) = sin 80°
sin 200° = sin(l 80° + 20°) = -sin 20°
The ascending order is
sin 200°, sin 0°, sin 50°, sin 100°

(iii) sin2x + sin6x – sin4x = 0
⇒ 2sin 4x cos2x – sin 4x = 0
⇒ sin 4x(2 cos 2x – 1) = 0
⇒ sin4x = 0 or (2cos2x – 1) = 0
⇒ 4x = nπ or cos2x = \(\frac{1}{2}\)

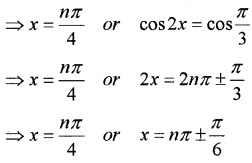
Plus One Maths Trigonometric Functions Practice Problems Questions and Answers

Question 1.
Convert the following degree measure into radian measure.
i)  45°
ii) 25°
iii) 240°
iv) 40°20′
v) -47°30′
Answer:

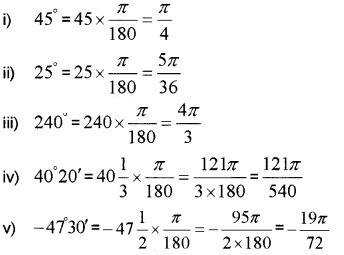
Question 2.
Convert the following radian measure into degree measure,
i)   6
ii) -4
iii) \(\frac{5 \pi}{3}\)
iv) \(\frac{7 \pi}{6}\)
v) \(\frac{11}{16}\)
Answer:

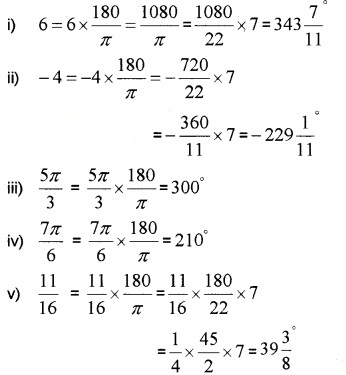
Question 3.
The minute hand of a watch is 1.5 cm long. How far does its tip move in 40 minutes? (Use π = 3.14)
Answer:
60 minutes = 360 degrees.
1 minutes = 6 degrees.
40 minutes = 240 degrees.
240° = 240 × \(\frac{\pi}{180}=\frac{4 \pi}{3}\)
The required distance travelled = l = rθ
= 1.5 × \(\frac{4 \pi}{3}\) = 2 × 3.14 = 6.28 cm

Question 4.
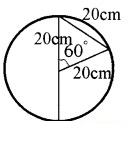
In a circle of diameter 40 cm, the length of a cord is 20 cm. Find the length of minor arc of the chord.
Answer:
The radius and chord join to form a equilateral triangle. Therefore
l = rθ = 20 × \(\frac{\pi}{3}\)
= 20 × \(\frac{3.14}{3}\) = 20.933.

Question 5.
If the arcs of the same lengths in the two circles subtend angles 65° and 110° at the centre, find the ratio of their radii.
Answer:
We have l = rθ, the radius and angle are inversely proportional. Therefore;

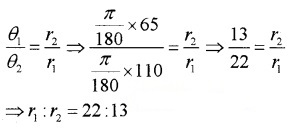
Question 6.
Find the values of the other five trigonometric functions in the following; (2 score each)

1. cos x = \(-\frac{3}{5}\), x lies in the third quadrant.
2. cot x = \(-\frac{5}{12}\), x lies in the second quadrant.
3. sin x = \(\frac{1}{4}\), x lies in the second quadrant.

Answer:
1. Given;
cos x = \(-\frac{3}{5}\)

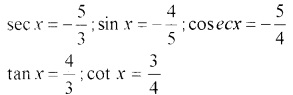
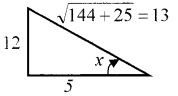
2. Given;
cot x = \(-\frac{5}{12}\)

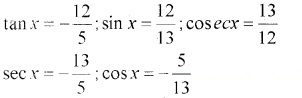
3. Given;
sin x = \(\frac{1}{4}\); cosecx = 4

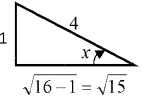
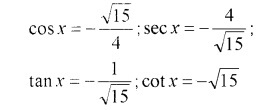
Question 7.
Find the value of the trigonometric functions. (2 score each)

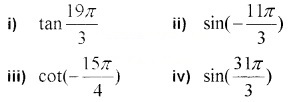
Answer:

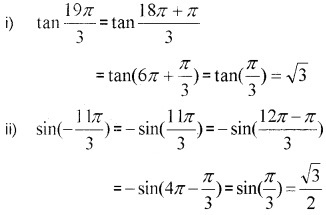
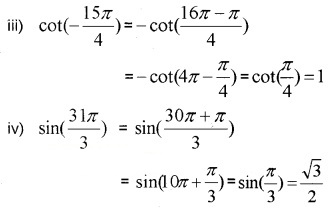
Question 8.
Find the value of the following.

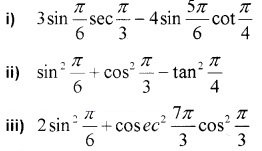
iv) sin 75°
v) tan 15°
Answer:

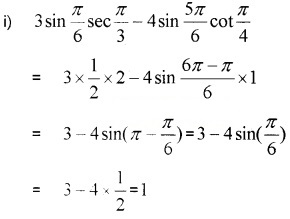
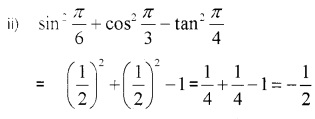
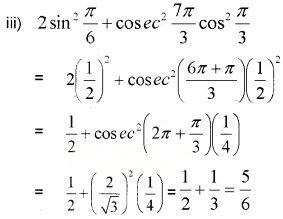
iv) sin 75° = sin(45° + 35°)
= sin 45° cos30° + cos45° sin 30°

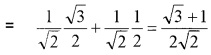
v) tan 15° = tan(45° – 30°) = \(\frac{\tan 45^{\circ}-\tan 30^{\circ}}{1+\tan 45^{\circ} \tan 30^{\circ}}\)

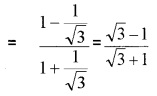
Question 9.
Find the principal and general solution of the following.

1. sin x = \(\frac{\sqrt{3}}{2}\)
2. cosx = \(\frac{1}{2}\)
3. tan x = \(\sqrt{3}\)
4. cos ecx = -2

Answer:
1. Given; sin x = \(\frac{\sqrt{3}}{2}\) = sin \(\frac{\pi}{3}\)
General solution is; x = nπ + (-1)ⁿ\(\frac{\pi}{3}\),
n ∈ Z
Put n = 0, 1 we get principal solution; x = \(\frac{\pi}{3} ; \frac{2 \pi}{3}\).

2. Given; cosx = \(\frac{1}{2}\) = cos \(\frac{\pi}{3}\)
General solution is; x = 2nπ ± \(\frac{\pi}{3}\), n ∈ Z
Put n = 0, 1 we get principal solution;
n = 0 ⇒ x = \(\frac{\pi}{3}\); n = 1 ⇒ x = 2π – \(\frac{\pi}{3}\) = \(\frac{5\pi}{3}\).

3. Given; tan x = \(\sqrt{3}\) = tan\(\frac{\pi}{3}\)
General solution is; ⇒ x = nπ + \(\frac{\pi}{3}\), n ∈ Z
Put n = 0, 1 we get principal solution;
n = 0 ⇒ x = \(\frac{\pi}{3}\); n = 1 ⇒ x = π + \(\frac{\pi}{3}\) = \(4\frac{\pi}{3}\).

4. Given; cosecx = -2
⇒ sin x = \(-\frac{1}{2}\) = – sin \(\frac{\pi}{6}\) = sin(-\(\frac{\pi}{6}\) )
General solution is; x = nπ – (-1)ⁿ \(\frac{\pi}{6}\), n ∈ Z
Put n = 1, 2 we get principal solution;

Plus One Maths Chapter Wise Questions and Answers