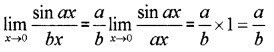Plus One Maths Chapter Wise Questions and Answers Chapter 13 Limits and Derivatives

Kerala Plus One Maths Chapter Wise Questions and Answers Chapter 13 Limits and Derivatives

Plus One Maths Limits and Derivatives Three Mark Questions and Answers

Question 1.
Evaluate the following: (3 score each)

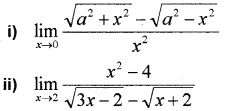
Answer:

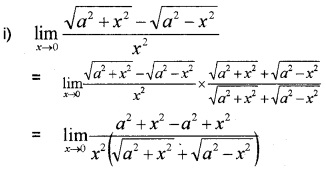
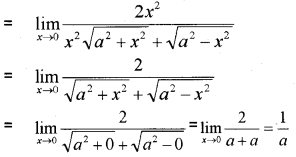
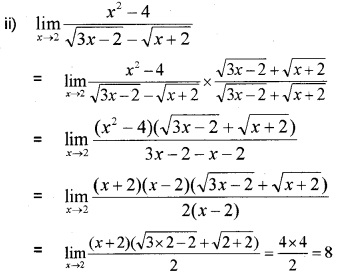
Question 2.
Evaluate the following: (3 score each)

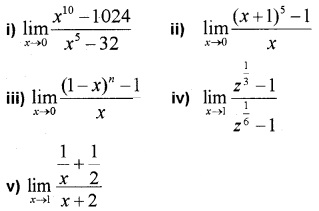
Answer:

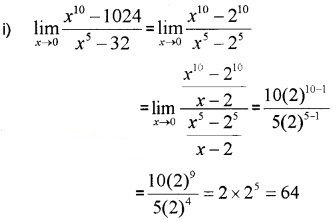
ii) Put x + 1 = y, x → 0, y → 1

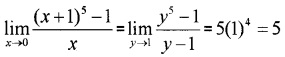
iii) Put 1 – x = y, x → 0, y → 1

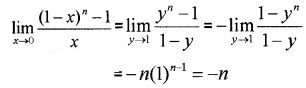
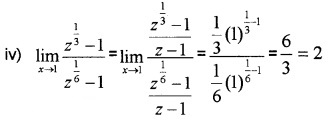
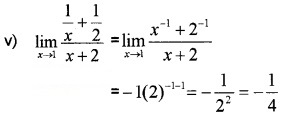
Question 3.
Evaluate the following: (3 score each)

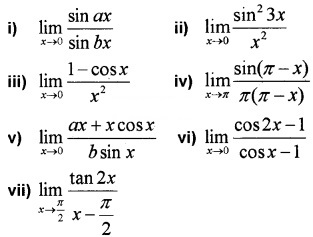
Answer:

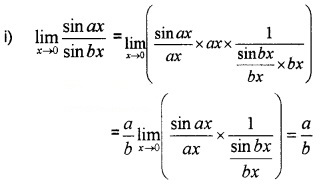
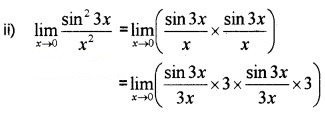
= 1 × 3 × 1 × 3 = 9

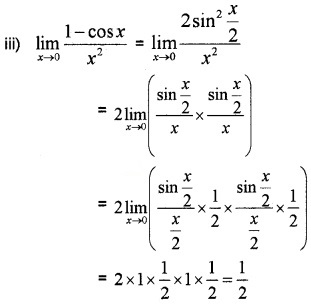
iv) Put π – x = y, x → π, y → 0

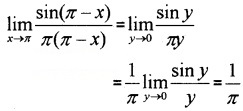
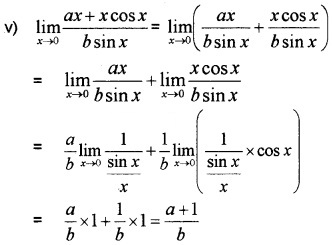
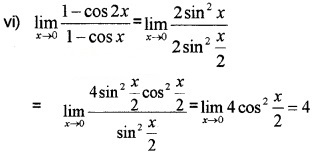
vii) Put x – $\frac{\pi}{2}$ = y, x → $\frac{\pi}{2}$, y → 0

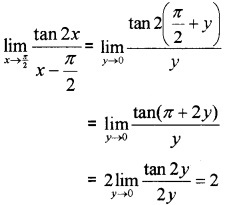
Question 4.
Evaluate the following: (3 score each)

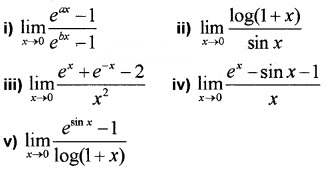
Answer:

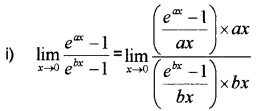
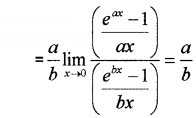
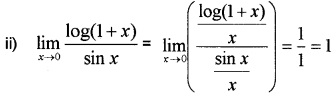
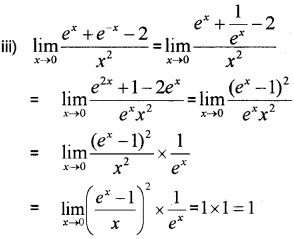
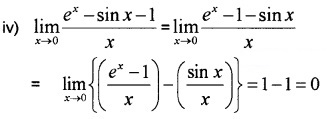
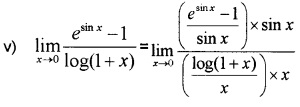
= $\frac{1}{1}$ × 1 = 1.

Question 5.
Find $\lim _{x \rightarrow 0} f(x)$ and $\lim _{x \rightarrow 1}$ f(x) where
f(x) = $\left\{\begin{array}{cc}{2 x+3,} & {x \leq 0} \\{3(x+1),} & {x>0} \end{array}\right.$.
Answer:

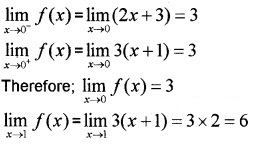
Question 6.
Find $\lim _{x \rightarrow 1}$f(x) where f(x) = $\left\{\begin{array}{cc} {x^{2}-1,} & {x \leq 1} \\{-x^{2}-1,} & {x>1}\end{array}\right.$.
Answer:

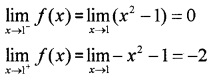
Therefore; $\lim _{x \rightarrow 1^{-}}$f(x) ≠ $\lim _{x \rightarrow 1^{-}}$f(x)
Hence $\lim _{x \rightarrow 1^{-}}$f(x) does not exist.

Question 7.
Evaluate

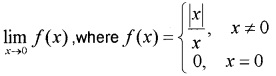
Answer:

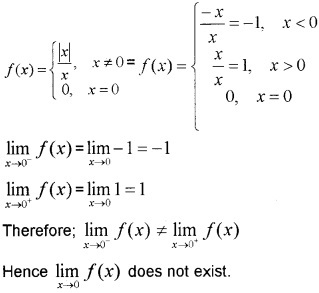
Plus One Maths Limits and Derivatives Practice Problems Questions and Answers

Question 1.
Evaluate the following:(2 score each)

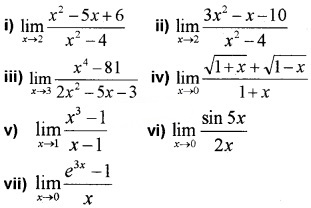
Answer:

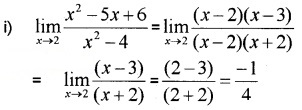
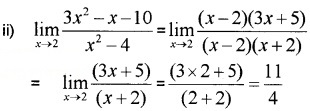
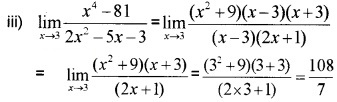
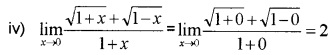
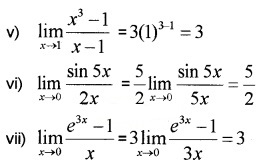
Question 2.
Find the derivatives of the following: (2 score each)

1. y = (x – d)(x – b)
2. y = (ax² + b)²
3. y = $\frac{x-a}{x-b}$
4. y = x^-3(5 + 3x)

Answer:
1.

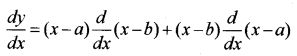
= (x – a) × 1 + (x – b) × 1
= x – a + x – b = 2x – a – b

2. y = a²x⁴ + b² + 2abx²
$\frac{d y}{d x}$ = 4a²x³ + 4abx.

3.

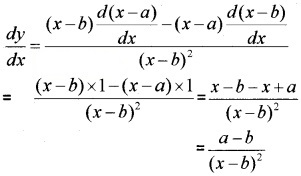
4. y = 5x^-3 + 3x^-2
$\frac{d y}{d x}$ = 5(-3)x^-3-1 + 3(-2)x^-2-1
= -15x^-4 – 6x^-3

Question 3.
Find the derivatives of the following: (3 score each)

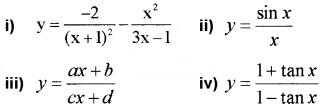
Answer:

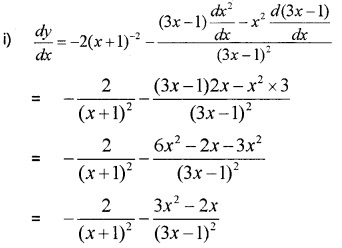
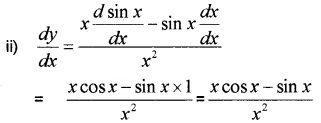
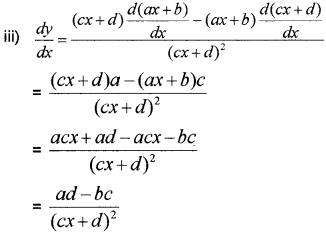
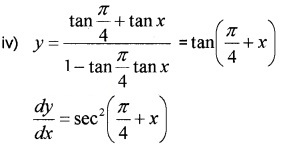
Question 4.
If xy = c² , prove that x² $\frac{d y}{d x}$ + c² = 0.
Answer:
xy = c² ⇒ y = $\frac{c^{2}}{x}$
Differentiating with respect to x;

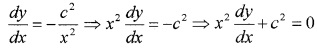
Question 5.
Evaluate: $\lim _{x \rightarrow 0} \frac{(x+5)^{2}-25}{x}$.
Answer:

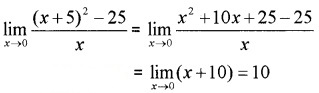
Question 6.
Find the derivative of f(x) = x sin x.
Answer:
f'(x) = x × cosx + sin x × 1 = xcosx + sinx.

Question 7.
Find the derivative of f(x) = $\frac{\sin x}{x}$.
Answer:

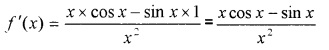
Question 8.
Evaluate $\lim _{x \rightarrow 0} \frac{\sin a x}{b x}$.
Answer:

Plus One Maths Chapter Wise Questions and Answers