A Plus Topper

Improve your Grades

Plus One Maths Chapter Wise Questions and Answers Chapter 1 Sets

by

Kerala Plus One maths Chapter Wise Questions and Answers Chapter 1 Sets

Plus One Maths Sets Three Mark Questions and Answers

Question 1.
There are 200 individuals with a skin disorder, 120 had been exposed to the chemical A, 50 to chemical B and 30 to both chemical A and B, Find the number of individuals exposed to

  1. Chemical A but not chemical B. (1)
  2. Chemical B but not chemical C. (1)
  3. Chemical A or chemical B. (1)

Answer:
1. Given; n(U) = 200; n(A) = 120;
n(B) = 50; n(A∩B) = 30
n (Chemical A but not chemical B)
= n(A ∩ B’) = n(A) – n(A ∩ B) = 120 – 30 = 90

2. n (Chemical B but not chemical A)
= n(A’ ∩ B) = n(B) – n(A ∩ B) = 50 – 30 = 20

3. n (Chemical A or chemical B)
= n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
= 120 + 50 – 30 = 140.

Question 2.
In a survey of 400 students in a school, 100 were listed as taking apple juice, 150 as taking orange juice and 75 were listed as taking both apple as well as orange juice. Find how many students were taking neither apple juice nor orange juice.
Answer:
Let A – Apple juice; O – Orange juice be the sets.
Given; n(U) = 400; n(A) = 100;
n(O) = 150; n(A ∩ O) = 75
n (neither apple juice nor orange juice)
= n(A’ ∩ O’) = n((A ∪ O)’)
= n(U) – n(A ∪ O)
= 400 – [n(A) + n(O) – n(A ∩ O)]
= 400 – [100 + 150 – 75] = 400 – 175 = 225.

Question 3.
In a committee, 50 people speak French, 20 speak Spanish and 10 speak both Spanish and French. How many speaks at least one of these two languages?
Answer:
Let F – French; S – Spanish be the sets.
Given; n(F) = 50; n(S) = 20;w(F ∩ S) = 10
n (speaks at least one of these two languages)
= n(F ∪ S) = n(F) + n(S) – n(F ∩ S)
= 50 + 20 – 10 = 60.

Question 4.
In a group of 65 people, 40 like cricket, 10 like both cricket and tennis, how many like tennis only and not cricket? How many like tennis?
Answer:
Let C – Cricket; T – Tennis be the sets.
Given;
n(C’ ∪ T) = 65; n(C) = 40; n(C ∩ T) = 10
n(C ∪ T) = n(C) + n(T) – n(C ∩ T)
⇒ 65 = 40 + n(T) – 10 ⇒ n(T) = 35
n (tennis only and not cricket)
= n(T ∪ C’) = n(T) – n(T ∩ C) = 35 – 10 = 25.

Question 5.
Let A and B be two sets such that n( A) = 20, n(A ∪ B) = 42, n(A ∩ B) = 4. Find

  1. n(B) (1)
  2. n(B – A) (1)
  3. n(A – B) (1)

Answer:

  1. n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
    ⇒ 42 = 20 + n(B) – 4 ⇒ n(B) = 26
  2. n(B – A) = n(B) – n(A ∩ B) = 26 – 4 = 22
  3. n(A – B) = n(A) – n(A ∩ B) = 20 – 4 = 16.

Question 6.
A = {x: x is a natural number less than 8}

  1. Write in roster form. (1)
  2. Write a subset of A containing all even numbers in A. (1)
  3. Which of the following could not be the number of elements of power set of a set [2, 8, 10, 16]? (1)

Answer:

  1. A = {1, 2, 3, 4, 5, 6, 7}
  2. {2, 4, 6} or {2, 4, 6, 7}
  3. 10. (since other are powers of 2.)

Plus One Maths Sets Four Mark Questions and Answers

Question 1.
Observe the Venn diagram.
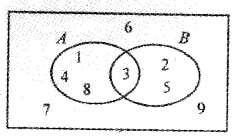
Plus One Maths Chapter Wise Questions and Answers Chapter 1 Sets 4M Q1

  1. Write in roster form. (1)
  2. Verify that (A – B) ∪ (A ∩ B) = A (2)
  3. Find (A ∩ B)’ (1)

Answer:

  1. A = {1, 3, 4, 8} ; B = {2, 3, 5}
  2. A – B = {1, 4, 8}; A ∩ B = {3}
    ⇒ (A – B) ∪ (A ∩ B) = {1, 3, 4, 8}
    Hence; (A – B) ∪ (A ∩ B) = A
  3. (A ∩ B)’ = {1, 2, 4, 5, 6, 7, 8, 9}

Plus One Maths Sets Practice Problems Questions and Answers

Question 1.
Write the following sets in roster form.

  1. A = {x: x xis an integer and -3 < x < 7}
  2. B = {x: x ∈ N; x ≤ 6}
  3. C = {x : x is a vowel in English alphabet}
  4. D = {x : x is a two-digit natural number such that the sum of its digits is 8}
  5. E = {x: x ∈ Z; \(-\frac{1}{2}<x<\frac{9}{2}\)}

Answer:

  1. A = {-2, -1, 0, 1, 2, 3, 4, 5, 6}
  2. B = {1, 2, 3, 4, 5, 6}
  3. C = {a, e, i, o, u}
  4. D = {17, 71, 26, 62, 35, 53}
  5. E = {1, 2, 3, 4}

Question 2.
Write the following sets in Set builder form.

  1. A = {3, 6, 9, 12}
  2. B = {2, 4, 8, 16, 32}
  3. C = \(\left\{\frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \frac{5}{6}, \frac{6}{7}\right\}\)
  4. D = {5, 25, 125, 625}
  5. E = {2, 4, 6……..} (1 score each)

Answer:

  1. A = {x: x = 3n, n ∈ N, n< 4 }
  2. B = {x: x = 2n; n ∈ N; n < 5 }
  3. C = {x: x = \(\frac{n}{n+1}\); n ∈ N, n ≤ 6}
  4. D = {x: x = 5n; n ∈ N, n ≤ 4 }
  5. E = {x: x is an even number}

Question 3.
Write the following in interval form.

  1. {x: x∈ R, -4 < x ≤ 6}
  2. {x: x∈ R, 0 ≤ x < 7 }
  3. {x: x∈ R, 3 ≤ x ≤ 4 } (1 score each)

Answer:

  1. (-4, 6]
  2. [0, 7)
  3. [3, 4]

Question 4.
Write the following in set builder form.

  1. [0, 10]
  2. [-2, 7)
  3. (3, 4)

Answer:

  1. {x: x∈ R, 0 ≤ x ≤ 10 }
  2. { x: x ∈ R, -2 ≤ x < 7 }
  3. {x: x ∈ R, 3 < x < 4 }

Question 5.
Find Set A, B and Universal set U (1 score each)
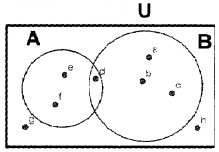
Plus One Maths Chapter Wise Questions and Answers Chapter 1 Sets Practice Questions Q5
Answer:
A = {e, f, d}; B = {a, b, c, d} and U = {a, b, c, d, e, f, g, h}

Question 6.
Write all subset of the following

  1. {1, 2}
  2. {a, b, c}
  3. Φ (1 score each)

Answer:

  1. Φ, {1}, {2}, {1, 2}
  2. Φ, {a}, {b}, {c} ,{a, b}, {a, c}, {b, c}, {a, b, c}
  3. Φ

Question 7.
Let A = {1, 2, {3, 4}, s, d, θ} , Which of the following statements are true/false and why?

  1. 3 ∈ A
  2. {1, {3, 4}} ∈ A
  3. {1, 2, 3} ⊂ A
  4. Φ ∈ A
  5. 1 ⊂ A (1 score each)

Answer:

  1. False
  2. True
  3. False
  4. False
  5. False

Question 8.
If A = {1, 2, 4, 6, 7, 8}; B = {2, 5, 7, 9, 10} and C = {4 , 5, 9, 10}. Find

  1. A ∪ B
  2. B ∪ C
  3. A ∪ C
  4. A ∩ B
  5. B ∩ C
  6. A∪ B ∪ C
  7. A ∩ B ∩ C
  8. (A ∩ B) ∪ (C ∩ A) (1 score each)

Answer:

  1. A ∪ B = {1, 2, 4, 5, 6, 7, 8, 9, 10}
  2. B ∪ C = {2, 4, 5, 7, 9, 10}
  3. A ∪ C = {1, 2, 4, 5, 6, 7, 8, 9, 10}
  4. A ∩ B = {2, 7}
  5. B ∩ C = {5, 9, 10}
  6. A ∪ B ∪ C = {1, 2, 4, 5, 6, 7, 8, 9, 10}
  7. A ∩ B ∩ C = Φ
  8. (A ∩ B) ∪ (C ∩ A) = {2, 7} u {4} = {2, 4, 7}

Question 9.
If A = {2, 4, 6, 7, 8, 12}; B = {2, 7, 9, 10} and C = {5, 9, 10, 12}. Find

  1. A – B
  2. B – C
  3. A – C
  4. B – A
  5. C – A
  6. (A ∪ B) – C
  7. A – {B ∩ C)
  8. (A ∩ B) – (C ∩ A) (1 score each)

Answer:

  1. A – B = {4, 6, 8, 12}
  2. B – C = {2, 7}
  3. A – C = {2, 4, 6, 7, 8}
  4. B – A = {9, 10}
  5. C – A = {5, 9, 10}
  6. (A ∪ B) – C = {2, 4, 6, 7, 8, 9, 10, 12} – {5, 9, 10, 12} = {2, 4, 6, 7, 8}.
  7. A – (B ∩ C) = {2, 4, 6, 7, 8, 12} – {9, 10} = {2, 4, 6, 7, 8, 12}
  8. (A ∩ B) – (C ∩ A) = {2, 7} – {12} = {2, 7}

Question 10.
If U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}; A = {2, 7, 9, 10} B = {5, 9, 10, 12} and C = {1, 4, 5, 7, 11}. Find

  1. A’
  2. B’
  3. A’ – C
  4. (B – A)’
  5. B’ ∩ C’
  6. (A ∪ B)’
  7. A’ ∩ B’ (1 score each)

Answer:

  1. A’ = { 1, 3, 4, 5, 6, 8, 11, 12}
  2. B’ = { 1, 2, 3, 4, 6, 7, 8, 11}
  3. A’ – C = {1, 3, 4, 5, 6, 8, 11, 12} – {2, 3, 6, 8, 9, 10, 12} = {1, 4, 5, 11}
  4. (B – A)’ = {5, 12}’ = {1, 2, 3, 4, 6, 7, 8, 9, 10, 11}
  5. B’ ∩ C’ = {1, 2, 3, 4, 6, 7, 8, 11} – {2, 3, 6, 8, 9, 10, 12} = {2, 3, 6, 8}
  6. (A ∪ B)’ = {2, 5, 7, 9, 10, 12}’ = {1, 3, 4, 6, 8, 11}
  7. A’ ∩ B’ = {1, 3, 4, 5, 6, 8, 11, 12} ∩ {1, 2, 3, 4, 6, 7, 8, 11} = {1, 3, 4, 6, 8, 11}

Question 11.
If X and Y are two sets such that X ∪ Y has 50 elements, X has 28 elements and Y has 32 elements, how many elements does X ∩ Y have?
Answer:
Given; n(X ∪ Y) = 50; n(X) = 28; n(Y) = 32
n(X ∪ Y) = n(X) + n(Y) – n(X ∩ Y)
⇒ 50 = 28 + 32 – n(X ∩ Y)
⇒ n(X ∩ Y) = 60 – 50 = 10

Plus One Maths Chapter Wise Questions and Answers