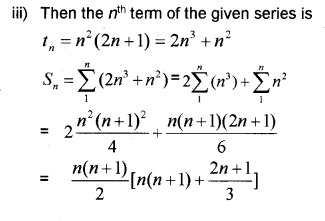Plus One Maths Chapter Wise Previous Questions Chapter 9 Sequences and Series

Kerala Plus One Maths Chapter Wise Previous Questions Chapter 9 Sequences and Series

Plus One Maths Sequences and Series 3 Marks Important Questions

Question 1.
Consider the GP 3,3²,3³, _______. (IMP-2014)
i) Find the sum to n terms of this GP.
ii) Find the value of n so that the sum to n terms of this GP is 120.
Answer:
i)

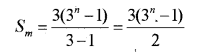
ii)

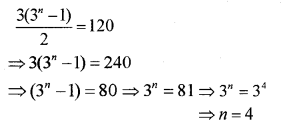
Plus One Maths Sequences and Series 4 Marks Important Questions

Question 1.
Given sum of three consecutive terms in an AP is 21 and their product is 280  (IMP-2011)
i) Find the middle term of the above terms.
ii) Find the remaining two terms of the above AP.
Answer:
i) Let the three consecutive terms be
a-d, a, a + d
a-d + a + a + d = 21
=>3a = 21
=>a = 7
ii) Then the AP becomes 7 – d,7, 7 + d
Given product is 280;
(7 – d)(7)(7 + d) = 280
=> (7 – d)(7 + d) = 40
==> 49 – d² = 40
=> <d² = 9 => d= 3,- 3
Therefore the AP is 4,7,10 or 10,7,4.

Question 2.
Consider the GP 3,6,12  (IMP-2011)
i) Which term of this GP is 96?
ii) Find the value of n so that sum to n terms of this GP is 381.
Answer:

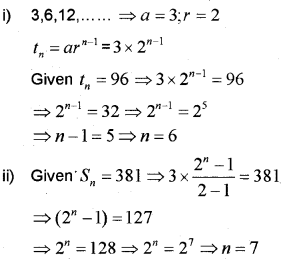
Question 3.
i) What is the sum of the first ‘n’ natural numbers?  (IMP-2012)
ii) Find the sum to ‘n’ terms of the series
3 x 8 + 6 x 11 + 9 x 14 + ______.
Answer:

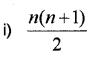
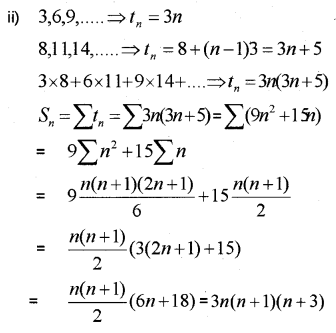
Question 4.
If the sum of the first n terms of an Arithmetic progression is ——,where X and Y are constants, find  (IMP-2012)
i) S₁ and S₂
ii) The first term and common difference.
iii) The n^th term.
Answer:
i) S₁ = X
S₂ =2X + 1/2(2 – 1)Y=2X + Y
ii) First term = a, = Sx = X
S₂ =2 X + Y
=> a₁ +a₂ =2 X + Y
=> a₂ =2X + Y
=>a₂ = X+ Y
Common difference =
a₂ – a₁ =X + Y – X = Y
iii) n^thterm = a_n = a + (n-1)d = X + (n – 1)Y

Question 5.
Find the sum to n terms of the series;  (IMP-2012)
2² + 5² + 8² +_______
Answer:

Question 6.
i) Write the first four terms of the sequence whose nth term \(a_{n}=\frac{n}{n+1}\) (MARCH-2013)
ii) The sum of the first three terms of a GP is \(\frac {12}{13}\) and their product is -1. Find the common ratio and the terms.
Answer:

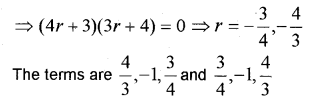
Question 7.
If the numbers \(\frac { 5 }{ 2 }\) x \(\frac { 5 }{ 8 }\) are three consecutive terms of a GP, then find x. (MARCH-2014)
Find the sum of the first n-terms of the series. 2 +22+222 + _____
Answer:

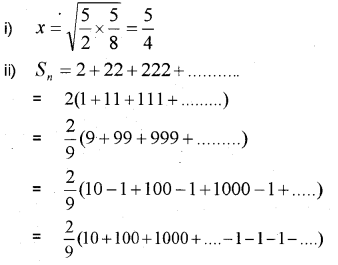
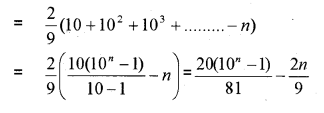
Question 8.
i) Find the 5^th term of the sequence whose nth term is \(a_{n}=\frac{n(n-2)}{(n+3)}\) (MARCH-2014)
ii) Write the sum of first n natural numbers.
iii) The 5^th, 8^th and 11^th terms of a GP are p, q and s respectively. Prove that q² – ps
Answer:

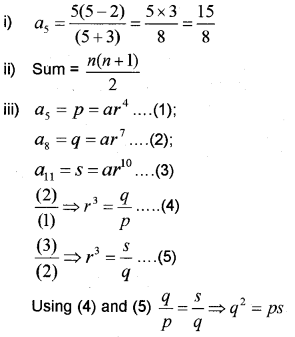
Question 9.
i) A man starts repaying a loan as a first instalment of Rs. 1,000. If he increases the instalment by Rs. 150 every month, what amount will he pay in the 30^th instalment?  (IMP-2014)
ii) Find the sum to n terms of the sequence:
7,77,777,7777 ______.
Answer:

Question 10.
i) Consider the AP 4,10,16,22…….. Find its common difference and the 7^th terms.  (IMP-2014)
ii) If the m^th term of an AP is \(\frac { 1 }{ n }\) and the nth term is \(\frac { 1 }{ m }\) , prove that the sum of the first ‘mn’ terms is \(\frac { 1 }{ 2 }\)(mn +1)
Answer:

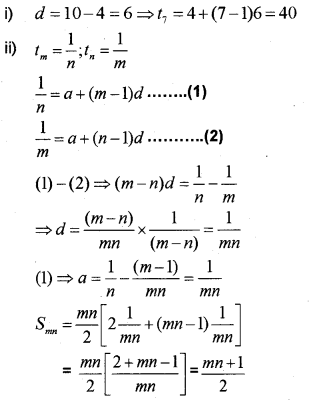
Question 11.
The 6^th term of the sequence whose n^th term is \(t_{n}=\frac{2 n-3}{6}\) is _____. (MARCH-2015)
a) 3
b) \(\frac { 1 }{ 2 }\)
c) \(\frac { 3 }{ 2 }\)
d) \(\frac { 1 }{ 3 }\)
ii) Find the sum to infinity of the sequence 1,\(\frac { 1 }{ 3 }\) ,\(\frac { 1 }{ 9 }\), ………
iii) If a, b, c are in AP and \(a^{\frac{1}{x}}=b^{\frac{1}{y}}=c^{\frac{1}{z}}\), prove that x, y, z are in AP.
Answer:

Plus One Maths Sequences and Series 6 Marks Important Questions

Question 1.
i) In an AP, the first term is 2 and the sum of the first five terms is one fourth the sum of the next five terms. (MARCH-2010)
a) Find the common difference.
b) Find the 20^th term.
ii) If AM and GM of two numbers are 10 and 8 respectively, find the numbers.
Answer:

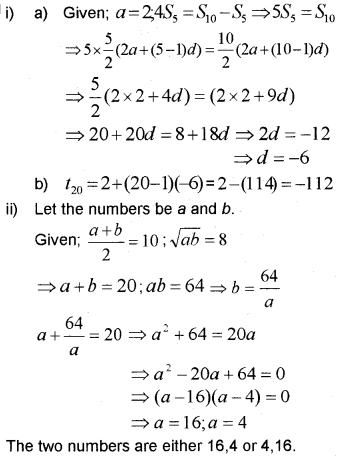
Question 2.
i) In an AP if m^th term is ‘n’ and nth term is ‘m’ .find the (m + n)^th term.  (IMP-2010)
ii) If 3^rd, 8^th and 13^th terms of a GP are x,y,z respectively, prove that x,y,z are in GP.
iii) Prove that x,y,z in the above satisfies the equation \(\frac{y^{10}}{(x z)^{5}}=1\)
Answer:

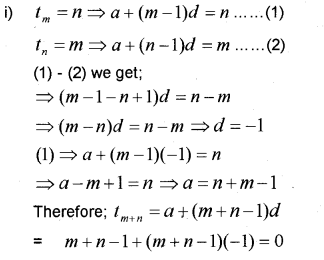
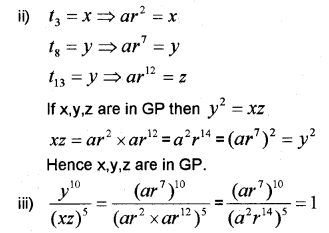
Question 3.
Which of the following is the n^th term of an AP? (MARCH-2011)
a) 3 – 2n
b)n² – 3
c) 3ⁿ – 2
d) 2 – 3n²
ii) Find the 10th term of the sequence
– 6,- \(\frac { 11 }{ 2 }\), – 5,….
iii) The sum of the first three terms of a GP is \(\frac { 39 }{ 10 }\) and their product is 1. Find the common ratio and the terms.
Answer:

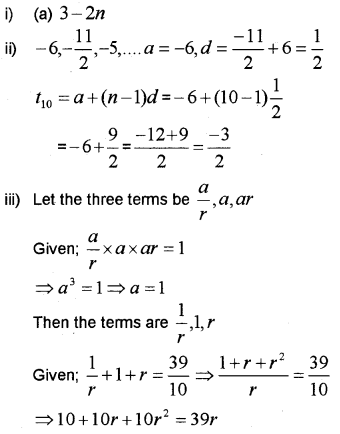
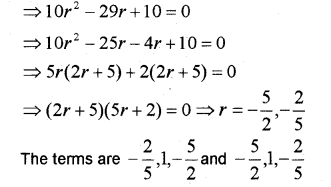
Question 4.
Find the 10^th term of an AP whose n^th \(\frac{2 n-3}{6}\) term is (MARCH-2012)
ii) Find the sum of the first 10 terms of the above AP.
iii) Find the sum of the first 10 terms of a GP, whose 3^rd term is 12 and 8^th term is 384.
Answer:

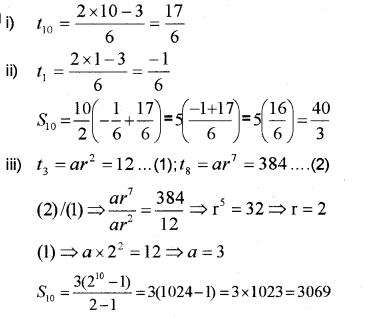
Question 5.
i) Find the 5^th term of the sequence whose n^th term, \(a_{n}=\frac{n^{2}-5}{4}\) (MARCH-2013)
ii) Find 7 + 77 + 777 +……. to n terms.
iii) Find the sum to n terms of the series.
1 x 2 + 2 x 3 + 3 x 4 + 4 x 5 + ………
Answer:

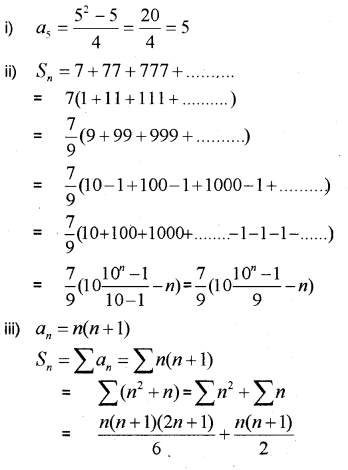
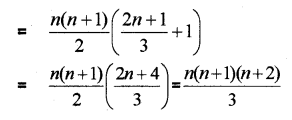
Question 6.
i) Find the sum of multiple of 7 between 200 and 400.  (IMP-2013)
ii) The sum of first 3 terms of a GP is \(\frac { 39 }{ 10 }\) and their product is 1. Find the terms.
Answer:

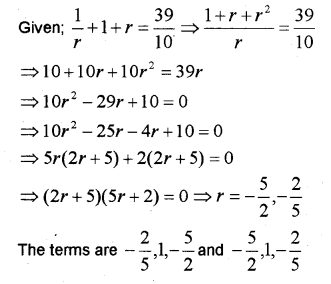
Question 7.
If ‘a’ is the first term and ‘cf is the common difference of an AP, then the nth term of the AP, a_n = ……. (MARCH-2014)
ii) In an AP, if the m^th‘ term is ‘n’ and the n^th term is ‘m’, where , prove that its p^th term is n + m – p.
iii) Find the sum to ‘n’ terms of the series:
1 x 2 + 2 x 3 + 3 x 4 + 4 x 5 + _______.
Answer:

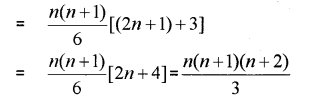
Question 8.
i) If the sum of certain number of terms of the AP 25,22,19 is 116, then find the last term.  (IMP-2014)
ii) Find the sum to n terms of the series
1 x 2 x 3 + 2 x 3 x 4 + 3 x 4 x 5 + ………
(Imp (Science) – 2014)
Answer:

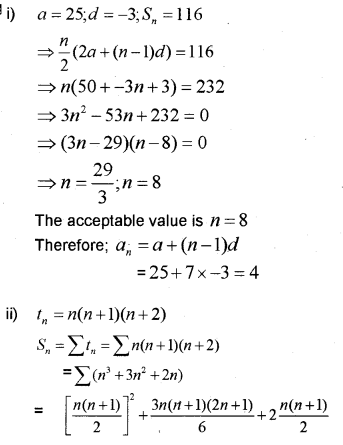
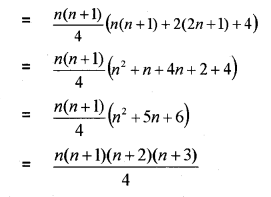
Question 9.
i) The 3^rd term of the sequence whose n^th term is (MARCH-2015)
ii) Insert three numbers between 1 and 256 so that the resulting sequence is a GP.
iii) If p^th term of an AP is q and q^th term is ‘p’, where p ≠ qfind r^th term.
Answer:

Question 10.
i) Geometric mean of 16 and 4 is ______.  (IMP-2015)
(a) 20
(b) 4
(c) 10
(d) 8
ii) Find the sum to n terms of the series: 5 + 55 + 555 + ________.
iii) Find the sum to n terms of the AP,
whose K^th term is a_k = 5K +1
Answer:

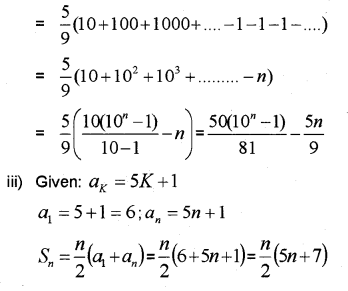
Question 11.
i) If the first three terms of an AP is x – 1,x + 1, 2x + 3, then x is  (IMP-2015)
(a)- 2
(b) 2
(c) 0
(d) 4
ii) Find the sum to n terms of the sequence.
1 x 2 + 2 x 3 + 3 x 4 + _______
iii) The nth term of the GP 5,- \(\frac { 5 }{ 2 }\),\(\frac { 5 }{ 4 }\),\(\frac { 5 }{ 8 }\),….. is \(\frac { 5 }{ 1024 }\) find ‘n’.
Answer:

Question 12.
The n^th term of the GP 5,25,125 (MARCH-2016)
is
(a) n⁵
(b) 5ⁿ
(c) (2n)⁵
(d) (5)²ⁿ
ii) Find the sum of .all natural numbers between 200 and 1000 which are multiples of 10.
iii) Calculate the sum of n-terms of the series whose n81 term is a_n = n(n + 3)
Answer:

Question 13.
i) Which among the following represents the sequence whose n^th terms is \(\frac { n}{ n+1 }\) ? (MAY-2017)
a) 1,2,3,4,5,6
b) 2,3,4,5,6
c) 2,\(\frac { 3 }{ 2 }\),\(\frac { 4 }{ 3 }\),\(\frac { 5 }{ 4 }\),\(\frac { 6 }{ 5 }\)
d) \(\frac { 1 }{ 2 }\),\(\frac { 2 }{ 3 }\),\(\frac { 3 }{ 4 }\),\(\frac { 4 }{ 5 }\),\(\frac { 5 }{ 6 }\)
ii) Using progression, find the sum of first five terms of the series 1 + \(\frac { 2 }{ 3 }\) + \(\frac { 4 }{ 9 }\) + …..
iii) Calculate: 0.6 + 0.66 + 0.666 + ………. n terms.
Answer:

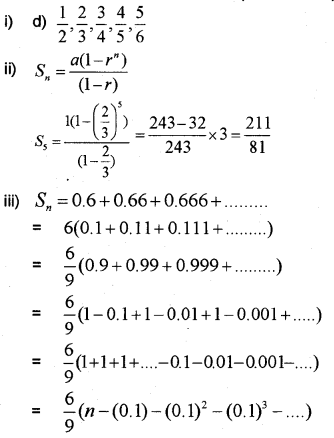
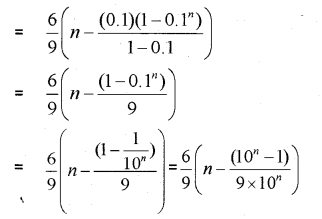
Question 14.
The sum of the infinite series is 1, \(\frac { 1 }{ 3 }\),\(\frac { 1 }{ 9 }\) ………is ________. (MARCH-2017)
(a) \(\frac { 3 }{ 2 }\)
(b) \(\frac { 5 }{ 2 }\)
(c) \(\frac { 2 }{ 3 }\)
(d) \(\frac { 7 }{ 2 }\)
ii) Find the sum of all natural numbers between 100 and 1000 which is a multiple of 5.
iii) Find the sum to n terms of the series 8,88,888 ………
Answer:

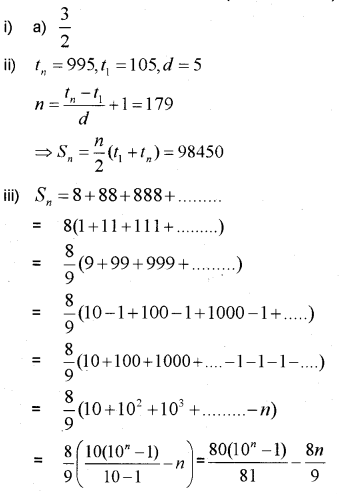
Question 15.
The 6^th term of the GP \(\frac { 1 }{ 2 }\),\(\frac { 1 }{ 4 }\),\(\frac { 1 }{ 8 }\), ………. (MARCH-2017)
a) \(\frac { 1 }{ 32 }\)
b) \(\frac { 1 }{ 64 }\)
c) \(\frac { 1 }{ 16 }\)
d) \(\frac { 1 }{ 128 }\)
ii) The sum of 1st 3 terms of a G.P is \(\frac { 13 }{ 12 }\) and their product is – 1. Find the common ratio and terms.
iii) Find the sum to n terms of the series \(3 \times 1^{2}+5 \times 2^{2}+7 \times 3^{2}\) + ………
Answer:

Plus One Maths Chapter Wise Previous Questions and Answer