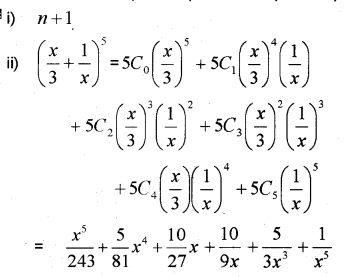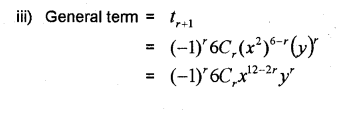Plus One Maths Chapter Wise Previous Questions Chapter 8 Binomial Theorem

Kerala Plus One Maths Chapter Wise Previous Questions Chapter 8 Binomial Theorem

Plus One Maths Binomial Theorem 3 Marks Important Questions

Question 1.
i) The number of terms in the expansion of $\left(\frac{x}{3}+9 y\right)^{10}$ is _____.(IMP-2013)
ii) Find the middle term in the above expansion.
Answer:
i) 11

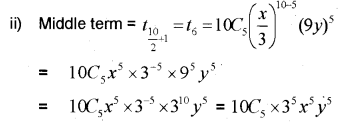
Question 2.
i) Find the general term in the expansion of (x + y)ⁿ
ii) Find the middle term in the expansion of $\left(2 x+\frac{1}{3 y}\right)^{18}$ (MARCH-2014)
Answer:

Question 3.
i) Write the general term in the expansion of (a + b)ⁿ 
ii) Find the 9th term in the expansion of $\left(\frac{x}{2}+\frac{6}{x^{2}}\right)^{12}$ (IMP-2014)
Answer:

Plus One Maths Binomial Theorem 4 Marks Important Questions

Question 1.
i) Find the general term in the expansion of $\left(3 x^{2}-\frac{1}{3 x}\right)^{9}$ (MARCH-2010)
ii) Find the term independent of x in the above expansion.
Answer:

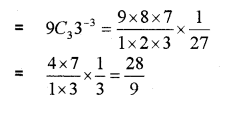
Question 2.
Consider the expansion of $\left(x^{2}-\frac{1}{3 x}\right)^{9}$ (IMP-2010)
i) Find the coefficient of x⁹
ii) Find the term which is independent of x.
Answer:

Question 3.
Consider the expansion of $\left(\frac{x}{9}+9 y\right)^{2 n}$ (MARCH-2011)
i) The number of terms in the expansion is _____
(a) 2n
(b) n+1
(c) 2n+1
(d) 2/7-1
ii) What is its (n+1)^th term?
iii) If n = 5, find its middle term.
Answer:

Question 4.
i) Write the general term in the expansion (1 + x)⁴⁴   
Write 21st and ,22nd terms in the expansion of (1 + x)⁴⁴
iii) If 21^st and 22^nd terms in the expansion of (1 + x)⁴⁴ are equal then find the value of x. (IMP-2011)
Answer:

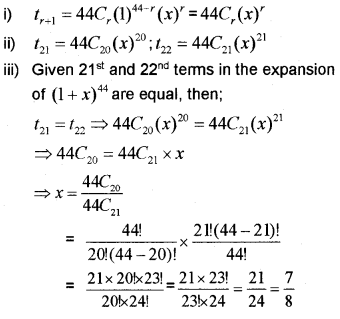
Question 5.
8. Find(x + y)⁴ – (x – y)⁴. (IMP-2012)
Hence evaluate: (√5 + √6)⁴ – (√5 – √6)⁴
Answer:

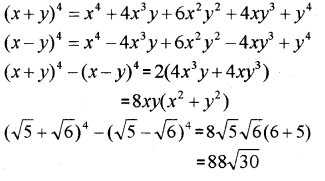
Question 6.
i) How many terms are there in the expansion of (1 + x)²ⁿ (n is a positive integer)? (IMP-2012)
ii) Show that the middle term in the (1 + x)²ⁿ
expansion of is $\frac{1.3 .5 \ldots(2 n-1)}{n !} 2^{n} x^{n}$
Answer:

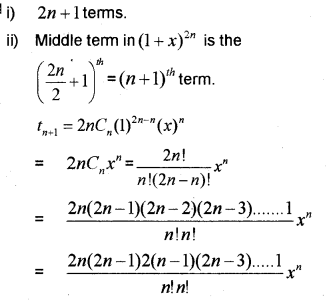
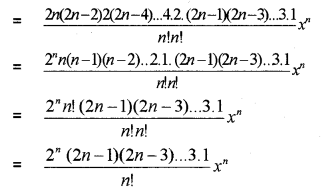
Question 7.
i) Find the general term in the expansion of $\left(\frac{x}{2}-\frac{2}{x}\right)^{10}$ (MARCH-2012)
ii) Find the terms independent of x in the above expansion.
Answer:

Question 8.
i) Find the number of terms in the expansion of $\left(x-\frac{1}{x}\right)^{14}$ (MARCH-2013)
ii) Find the general term in the expansion of $\left(x-\frac{1}{x}\right)^{14}$
iii) Find the term independent of x in the above expansion.
Answer:
i) 15

Question 9.
i)Write the number of terms in the expansion of (a -b)²ⁿ
ii) Find the general term in the expansion of $\left(x^{2}-y x\right)^{12}, x \neq 0$ (MARCH-2014)
iii) Find the coefficient of x⁶y³ in the expansion of (x + 2y)⁹
Answer:

Question 10.
i) Write the expansion of (a + n)ⁿ, where n is any positive integer. (IMP-2014)
ii) Find the value of ‘a’ if the 17^th term and 18^th term in the expansion of (2 +a)⁵⁰ are equal.
Answer:

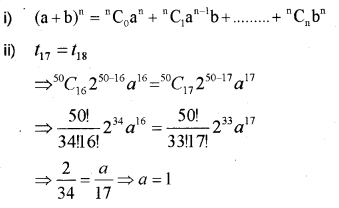
Question 11.
i) The number of term in the expansion of $\left(x-\frac{1}{x}\right)^{2 n}$ is ______. (MARCH-2015)
(a) n+1
(b) n
(c) 2n+1
(d) 2n+2
ii) Find a, if the 17^th term and 18^th term of the expansion of (2 +a)⁵⁰ are equal.
Answer:

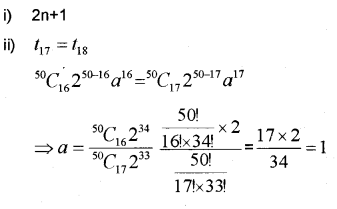
Question 12.
i) Number of terms in the expansion of $\left(x+\frac{1}{x}\right)^{20}$ (IMP-2016)
(a) 19
(b) 20
(c) 21
(d) 22
Consider the expansion of $\left(3 x^{2}-\frac{1}{3 x}\right)^{9}$
find the coefficient of x⁶ and the term independent of x.
Answer:

Question 13.
The 8th term in the expression (MARCH-2016)
of(√2 + √3)⁷ is
a) 27√2
b) 27√3
c) 72√2
d) 72√3
ii) Find the term independent of x in the expansion of $\left(x+\frac{1}{2 x}\right)^{18} ; x>0$
Answer:

Question 14.
Write the expansion of (a + b)^{4  (MAY-2017)}
Evaluate: (√5 + √6)4+ (√5 – √6)⁴
Answer:

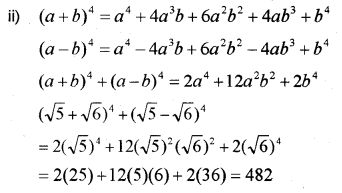
Question 15.
Consider the expansion of $\left(x+\frac{1}{x}\right)^{10}$ (MARCH-2017)
i) The number of terms in the expansion is _____.
(a) 10
(b) 9
(c)11
(d) 12
ii) Find the term which is independent of x in the above expansion.
Answer:

Plus One Maths Binomial Theorem 6 Marks Important Questions

Question 1.
i) Write the number of terms in the expansion of (a + b)ⁿ
ii) Expand $\left(\frac{x}{3}+\frac{1}{x}\right)^{5}$ (MARCH-2013)
iii) Find the general term in the expansion of $\left(x^{2}-y\right)^{6}$
Answer:

Plus One Maths Chapter Wise Previous Questions and Answer