Plus One Maths Chapter Wise Previous Questions Chapter 5 Complex Numbers and Quadratic Equations

Kerala Plus One Maths Chapter Wise Previous Questions Chapter 5 Complex Numbers and Quadratic Equations

Plus One Maths Principle of Complex Numbers and Quadratic Equations 3 Marks Important Questions

Question 1.
Find the modulus and argument of the complex number \(\frac{1+i}{1-i}\) . Find its multiplicative inverse in the form a + ib (IMP-2012)
Answer:
Convert into a + ib form

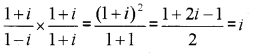
Hence Modulus is 1 and argument is \(\frac{\pi}{2}\)
Multiplicative inverse of i is \(\frac{1}{i}=\frac{1}{i} \times \frac{-i}{-i}=-i\)

Plus One Maths Principle of Complex Numbers and Quadratic Equations 4 Marks Important Questions

Question 1.
i) Express the complex number \(z=\frac{5 + i}{2 + 3i}\) in the form of a + ib. (MARCH-2010)
ii) Represent z in the polar form.
Answer:

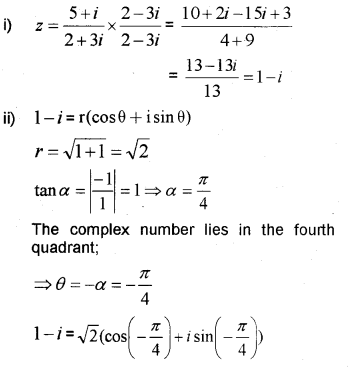
Question 2.
consider the complex number (MARCH-2011)

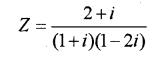
i) Express z in the form of a + ib
ii) Represent z in the polar form.
Answer:

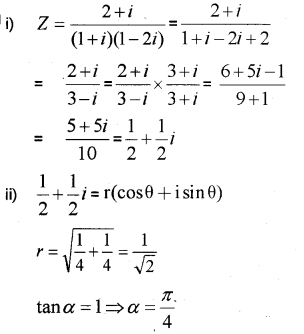
The complex number lies in the first quadrant;

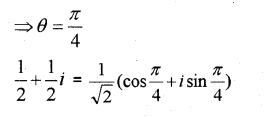
Question 3.
i) Express \(\frac{1}{1-i}\) in the form of a + ib  (IMP-2011)
ii) Express \(\frac{1}{1-i}\) in the polar form.
Answer:

Question 4.
Represent the complex number 1 + i√3 in the polar form.  (IMP-2012)
Express \(\frac{2 + i}{2 – i}\) in the form of a + ib.
Answer:

Question 5.
Consider the complex number  (MARCH-2012)

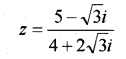
i) Express complex number in the form of a + ib.
ii) Express complex number in the polar form
Answer:

Question 6.
i) Express the following complex number in the form a + ib  (MARCH-2013)
(1 +i) – (1 – 6i) + (2 + i)
ii) Represent the complex number z = 1 + i in the polar form.
Answer:

Question 7.
i) Represent the complex number √3+ i in the polar form.  (MARCH-2013)
ii) Solve : √5x² + x + √5 = 0
(March (Science) – 2013)
Answer:

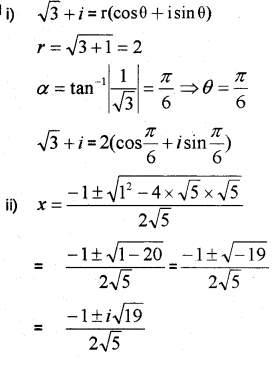
Question 8.
i) Express \(\frac{1+i}{1-i}\) in the form a + ib.  (IMP-2013)
ii) Represent the \(\frac{1+i}{1-i}\) in the polar form.
Answer:

Question 9.
i) Solve the quadratic Equation – x² + x – 2 = 0  (IMP-2014)
ii) Express ‘i’ in the form r(cosθ+i sinθ )
Answer:

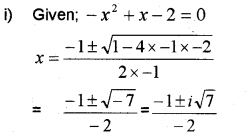
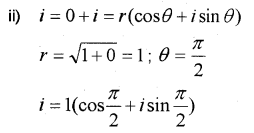
Plus One Maths Principle of Complex Numbers and Quadratic Equations 6 Marks Important Questions

Question 1.

a) a + ib form. (IMP-2010)
b) polar form.
Answer:

Question 2.
i) If z = √3 + i , find the conjugate of Z. (IMP-2010)
ii) Write the polar form of the complex number z = √3 + i
iii) Solve 2x² + 3x + 1 = 0
Answer:

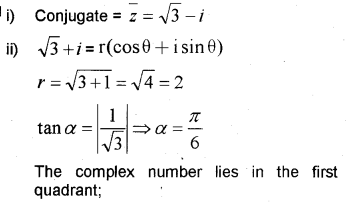
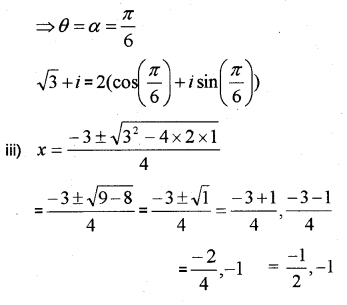
Question 3.
i) Solve: √3x² + x + √3 = 0 (MARCH-2014)
ii) Represent the complex number z = 1 + i √3 in the polar form.
Answer:

Question 4.
The conjugate of 1 – 2i is _______. (IMP-2014)
ii) Express the complex number \(\frac{2 + 3i}{1 – 2i}\) in the form a + ib .
iii) Solve x² + 3x + 5 = 0
Answer:

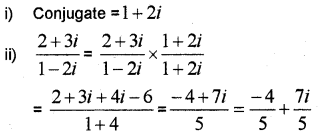
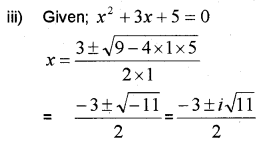
Question 5.
i) Represent the complex number 1 + √3i in the polar form. (MARCH-2015)
ii) Find the square root of the complex number – 7 – 24i.
Answer:

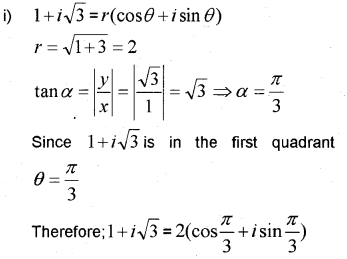
ii)

Since the product xy is negative, we have x = 3, y = – 4 or, x = – 3, y = 4
Thus, the square roots of – 7 – 24i are 3 – 4i and – 3 + 4i.

Question 6.
i) What is i ^{– 35} ? (IMP-2015)
a) i
b) -i
c) 1
d) -1
ii) Express the complex number √3 + i ’ in the polar form.
iii) Solve: √5x² + x + √5 = 0
Answer:
i) a) i
ii)

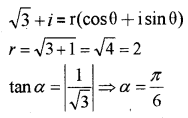
The complex number lies in the first quadrant;

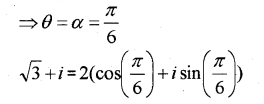
iii)

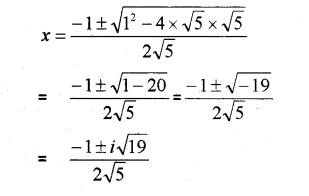
Question 7.
i) Which one of the following is the real part and imaginary part of the complex number: (MARCH-2016)

a) 0 and 1
b) 0 and 2
c) 3 and 2
d) 0 and 4
ii) Express the complex number ‘ i ’ in the polar form.
iii) Solve: √5x² + x + √5 = 0
Answer:
i) b) 0 and 2
ii)

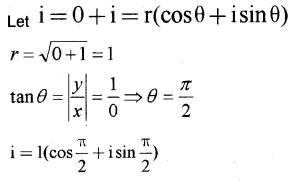
iii)

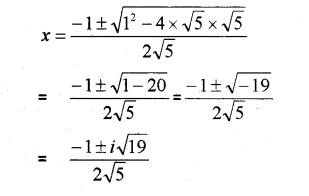
Question 8.
i) Write the real and imaginary part of the complex number – 3 + √- 7 (MAY-2017)
ii) Find the modulus and argument of the complex number 1 + i√3
iii) Solve: x² – 2x + 3 = 0
Answer:
i) Real part is – 3 and imaginary part is √7
ii)

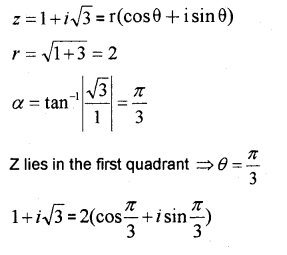
iii)

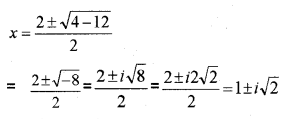
Question 9.
i) i¹⁸= ________
a) 1
b) 0
c) – 1
d) i
ii) complex number in polar form √3 + i
iii) Find the square root of the complex number – 8 – 6i.
Answer:
i) c) – 1
ii)

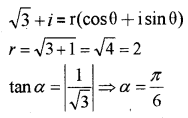
The complex number lies in the first quadrant;

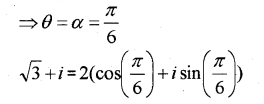
iii)

Since the product xy is negative, we have x = 1, y = – 3 or, x = – 1, y = 3 Thus, the square roots of – 8 – 6i are 1 – 3i and – 1 + 3i.

Plus One Maths Chapter Wise Previous Questions and Answer