Kerala Plus One Maths Chapter Wise Previous Questions Chapter 3 Trigonometric Functions
Plus One Maths Trigonometric Functions 3 Marks Important Questions
Question 1.
i) Find the degree measure corresponding to \(\frac { 11 }{ 14 }\) radians.( use π = \(\frac { 22 }{ 7 }\)) (MARCH-2010)
ii) If cos x = \(\frac { -1 }{ 2 }\), x lies in the third quadrant,find sin x and tan x
Answer:
i) Degree measure corresponding to \(\frac { 11 }{ 14 }\) radians
= \(\frac{11}{14} \times \frac{180}{\pi}=\frac{11}{14} \times \frac{180 \times 7}{22}=\frac{1}{2} \times \frac{180}{2}=45^{\circ}\)
ii) since x lies in the third quadrant
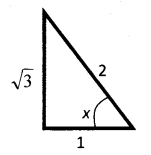
sin x = –\(\frac{\sqrt{3}}{2}\)
tan x = √3
Question 2.
prove that (MARCH-2010)
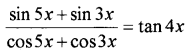
Answer:
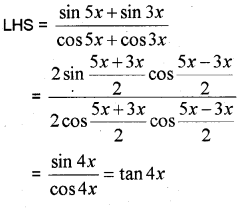
Question 3.
Showthat (cos x + cos y)² +(sin x + sin y)² =\(4 \cos ^{2}\left(\frac{x-y}{2}\right)\) (MARCH-2011)
Answer:
(cos x + cos y)² + (sin x + sin y)²
= cos² x + cos² y + 2cosx cosy + sin² x + sin² y + 2 sin x sin y
= 1+ 1 + 2(cosxcosy + sinxsiny)
= 2 + 2cos(x – y) = 2(1 + cos(x – y))
= \(4 \cos ^{2}\left(\frac{x-y}{2}\right)\)
Question 4.
prove that (MARCH-2013)
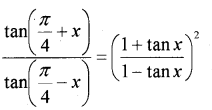
Answer:
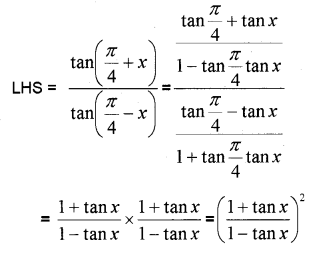
Question 5.
Consider the trigonometric equation tan x = √3 (IMP-2013)
i) Write the general solution.
ii) Write the principal solution.
Answer:
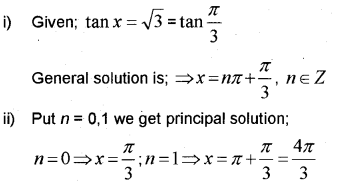
Question 6.
i) The value of sin(π – x) is _______. (MARCH-2014)
ii) Find the principal and general solution of the equation sin x = \(\frac { √3 }{ 2 }\)
Answer:
i) sin x
ii)
Question 7.
prove that (MARCH-2014)
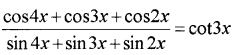
Answer:
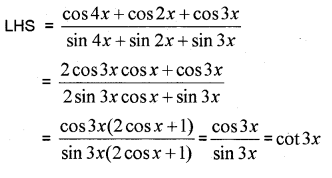
Question 8.
i) 1 + tan² x = _______. (IMP-2014)
ii) If sin x = \(\frac { 3 }{ 5 }\) and x lies in the second quadrant, find the values of cosx, tan x and secx.
Answer:
i) sec² x
ii)
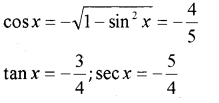
Plus One Maths Trigonometric Functions 4 Marks Important Questions
Question 1.
Expand cos(x + y) and hence prove (IMP-2010)
i) cos 2x = 1 – 2sin² x
ii) Solve the equation tan² θ + cot² θ = 2
Answer:
i) cos(x + y) = cos x cos y — sinx sin y
Put y = x
cos(x + x) = cos x cosx – sin x sin x
=> cos(2x) = cos² x – sin² x
=> cos(2x) = 1 – sin² x – sin² x = 1 – 2sin² x
ii)
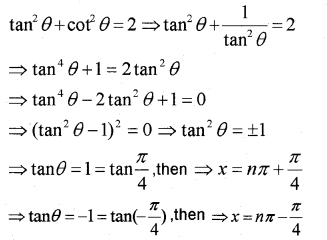
Question 2.
Show that (IMP-2010)
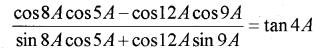
Answer:
Question 3.
i) Find the value of sin(\(\frac { 31π }{ 3 }\)) (MARCH-2011)
ii) Find the principle and general solution of the equation cos x = \(\frac {-√3 }{ 2 }\)
Answer:
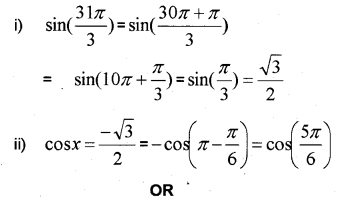
Question 4.
Solve: sin 2x – sin 4x + sin 6x = 0 (IMP-2012)
Answer:
sin 2x + sin 6x – sin 4x = 0
=> 2sin4xcos2x – sin4x = 0
=> sin4x(2cos2x – 1) = 0
=>sin4x = 0 or (2cos2x – 1) = 0
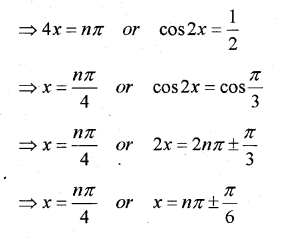
Question 5.
tan x tan 2x tan 3x = tan 3x – tan 2x – tan x (IMP-2012)
Answer:
We have; 3x= 2x + x
Take tan on both sides;
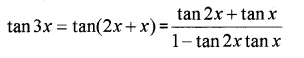
tan 3x(1 – tan 2x tan x) = tan 2x + tan x
tan 3x- tan 3x tan 2x tan x = tan 2x + tan x
tan x tan 2x tan 3x = tan 3x – tan 2x – tan x
Question 6.
i) Evaluate tan(\(\frac {13π }{ 6 }\)) (MARCH-2012)
ii) If tan x = \(\frac {1 }{ 2 }\) and x is in the third quadrant, find sinx and cosx.
Answer:
Question 7.
Prove that (MARCH-2012)
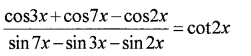
Answer:
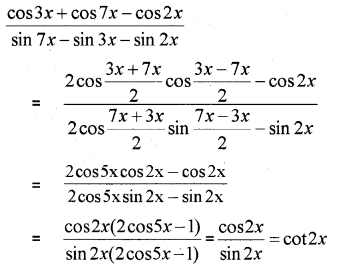
Question 8.
i) \(\frac {tan x + tan y}{ 1 – tan x tan y }\) = _________. (MARCH-2013)
ii) Prove that
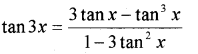
Answer:
i) tan(x + y)
ii)
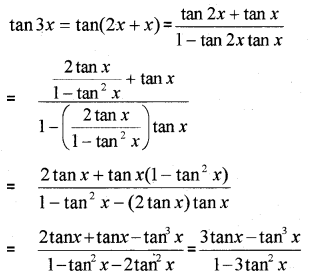
Question 9.
Match the following: (MARCH-2013)
Answer:
Question 10.
i) Prove that (MARCH-2013)
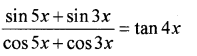
ii) Prove that
Answer:
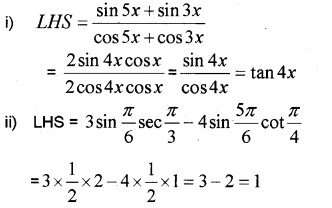
Question 11.
Show that (IMP-2013)
i) tan 15°=2-√3
ii) tan 15°+cot 15° = 4
Answer:
i)
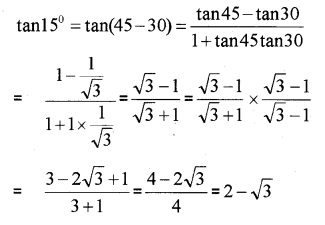
ii)
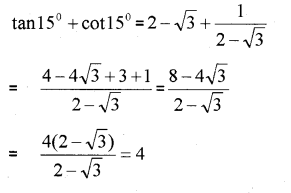
Question 12.
i) Prove that (MARCH-2014)
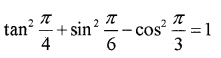
ii)
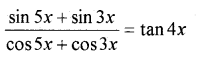
Answer:
i)
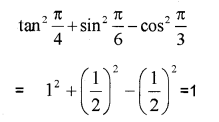
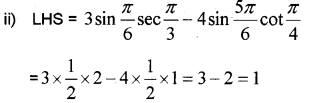
Question 13.
i) If tan x = \(\frac {3 }{ 4 }\); x lies in the third quadrant,
find the value of cos x. (MARCH-2014)
ii) Find the principal and general solution of cos x = \(\frac {1 }{ 2 }\)
Answer:
i) Since x lies in the third quadrant
Plus One Maths Trigonometric Functions 6 Marks Important Questions
Question 1.
i) Write the value of (IMP-2011)
sin 600°; cos 330°; cos 120°; sin 150°
ii) Prove that
sin 600° cos330° +cos120° sin 150° + sin 180° cos 180° = -1
Answer:
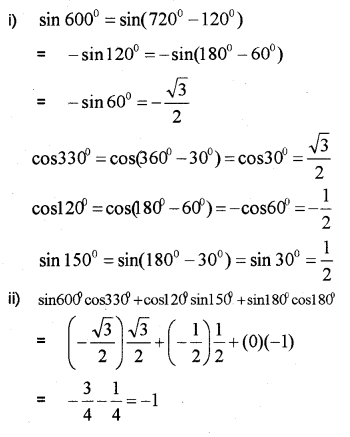
Question 2.
i) Find the value of sin 75° (IMP-2012)
ii) Prove that
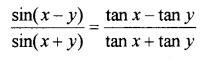
Answer:
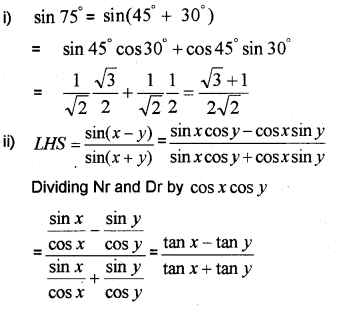
Question 3.
i) \(\frac {2π }{ 3 }\) radians = ______ degree.(IMP-2014)
ii) cos(2π – x) = _______
iii) Find the general solution of sin 2x – sin 4x + sin 6x = 0
Answer:
i) 120°
ii) cos x
iii)
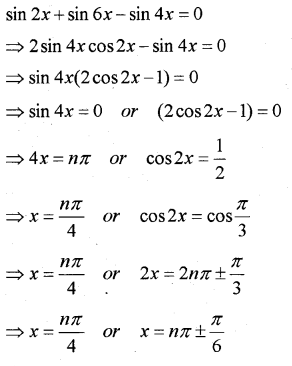
Question 4.
i) sin x cos y + cos x sin y = ______. (IMP-2014)
ii) Find sin 50° cos 10° + cos50° sin10°
iii) Prove that
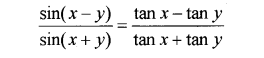
Answer:
i) sin(x + y)
ii) sin 50° cos 10° + cos 50° cos 10°
= sin(50° +10°) = sin(60°) = \(\frac {√3 }{ 2 }\)
iii)
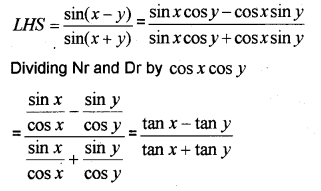
Question 5.
i) Which one of the following values of sin x is incorrect? (MARCH-2015)
a) 0
b) \(\frac {1 }{ 2 }\)
c) 3
d) 1
ii) Prove that
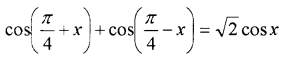
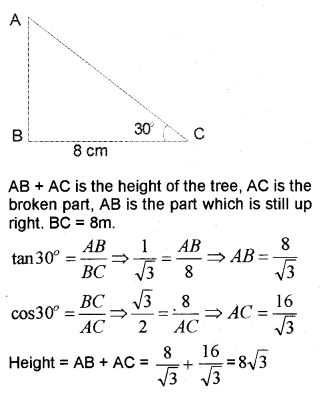
iii) A tree breaks due to a storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Answer:
i) 3
ii)
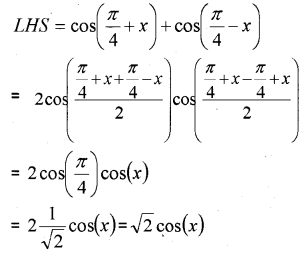
iii)
Question 6.
i) sin 225° = _______.(MARCH-2015)
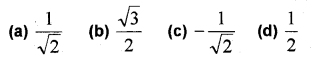
ii) Find the principle and general solutions of sin x = – \(\frac {√3 }{ 2 }\)
iii) Prove that
Answer:
i) \(\frac {- 1 }{ √2 }\)
ii)
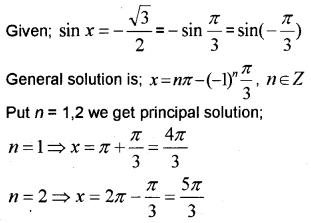
iii)
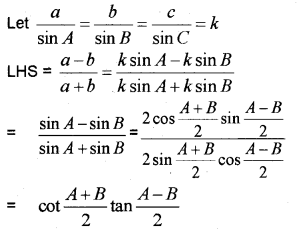
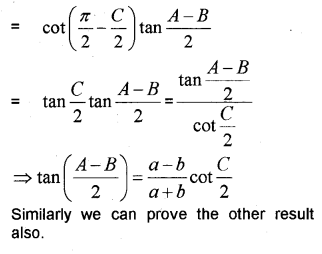
Question 7.
i) Which of the equal to 520° ? (IMP-2015)
ii) Solve Sin 2x – Sin 4x + Sin 6x = 0.
iii) In any triangle ABC, prove that
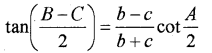
Answer:
i) \(\frac { 26π }{ 6 }\)
ii)
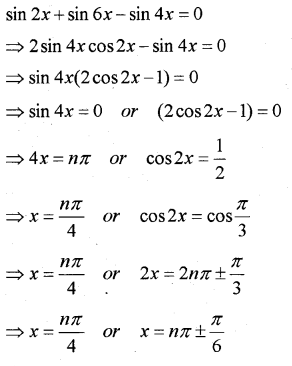
iii)
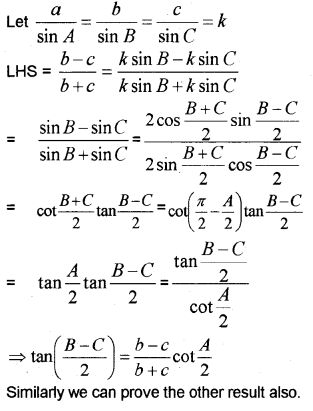
Question 8.
i) The degree measure of \(\frac { 7π }{ 6 }\) radian is _____. (MARCH-2016)
(a) 120° (b) 102° (c) 201° (d) 210°
ii) Prove that
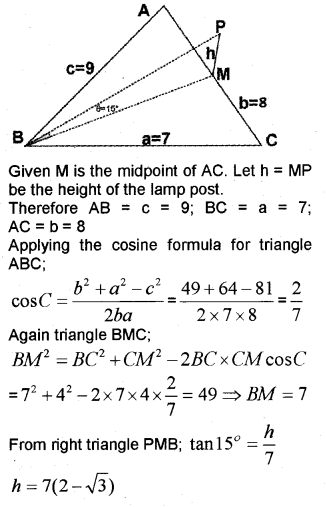
iii)A lamp post is situated at the middle point M of the side AC of a triangular plot ABC with BC = 7m, CA = 8m, AB =9m. Lamp post subtends an angle 15° at the point B. Determine the height of the lamp post.
Answer:
i) 210°
ii)
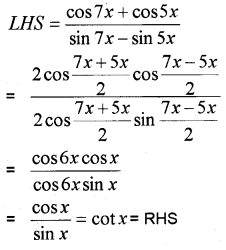
iii)
Question 9.
i) 40°20′ = ____ radians (MAY-2016)
a) \(\frac { 112π }{ 540 }\)
b) \(\frac { 211π }{ 540 }\)
c) \(\frac { 122π }{ 540 }\)
d) \(\frac { 121π }{ 540 }\)
ii) Prove that
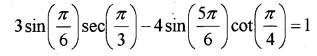
iii) Solve sin 2x – sin 4x + sin 6x = 0
Answer:
i)
d) \(\frac { 121π }{ 540 }\)
ii)
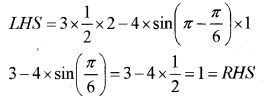
iii)
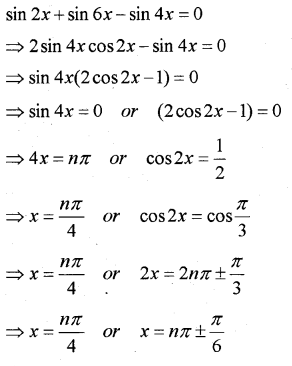
Question 10.
i) sin 405°= _____. (MARCH-2017)
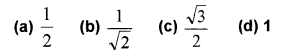
ii)
sin x = \(\frac { 3 }{ 5 }\)
x lies in the second quadrant.Find the values of cosx,secx,tanx,cotx
iii) Solve: sin 2x – sin 4x + sin 6x = 0
Answer:
i) a) \(\frac { 1 }{ 2 }\)
ii)
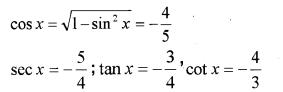
iii)
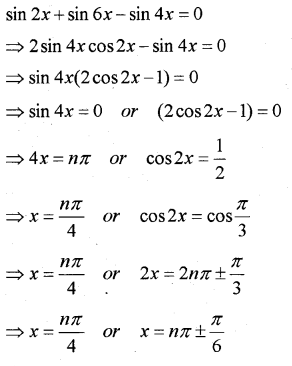
Question 11.
i) \(\frac { 7π }{ 6 }\) radian = ______ degree. (MARCH-2017)
a) 200
b) 300
c) 240
d) 120
ii) Find the value of tan 75°
iii) In a triangle ABC, prove that
a sin(B – C)+b sin(C -A)+c sin (A – B) = 0
Answer:
i) a) 210
ii)
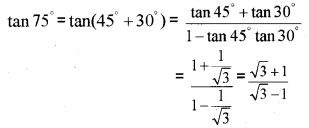
iii)
