Plus One Maths Chapter Wise Previous Questions Chapter 13 Limits and Derivatives

Kerala Plus One Maths Chapter Wise Previous Questions Chapter 13 Limits and Derivatives

Plus One Maths Limits and Derivatives 3 Marks Important Questions

Question 1.
Find the derivative of y = tan x from first principles. (MARCH-2010)
Answer:

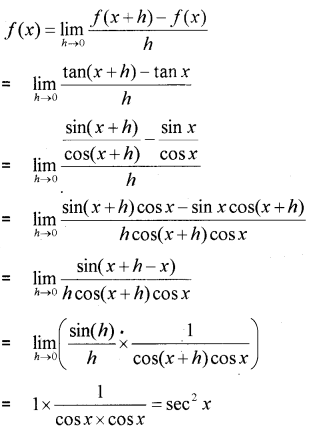
Question 2.
Choose the most appropriate answer from those given in the bracket (IMP-2010)

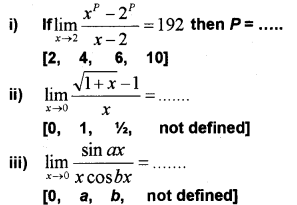
Answer:

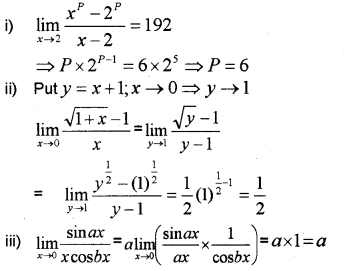
Question 3.

(IMP-2010)
Answer:

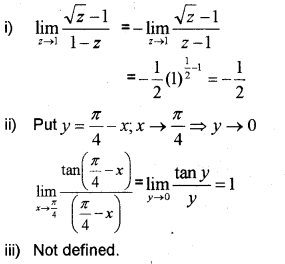
Question 4.
Using the first principle of derivatives, find the derivatives of \(\frac { 1 }{ x }\) (MARCH-2011)
Answer:

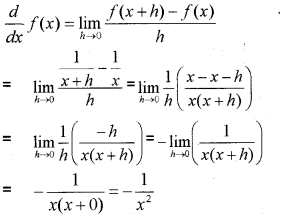
Question 5.
Using the quotient rule find the derivative mof f(x) = cot x (MARCH-2011)
Answer:

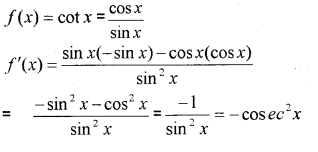
Question 6.
Find the derivatives of the following: (MARCH-2011)

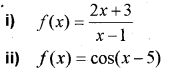
Answer:

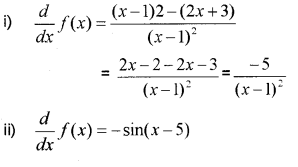
Question 7.
Prove that (MARCH-2012)

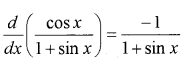
Answer:

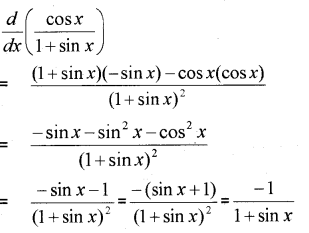
Question 8.
Find the derivative of y = cotx from first principles. (MARCH-2012)
Answer:

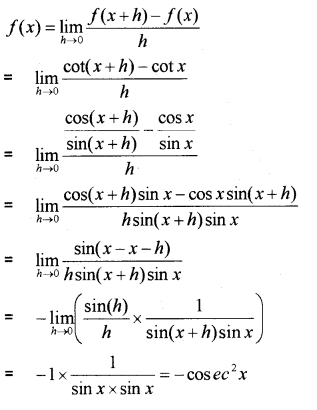
Question 9.
i) The value of \(\lim _{x \rightarrow 0} \frac{\sin x}{x}\) (MARCH-2013)
ii) Evaluate \(\lim _{x \rightarrow 0} \frac{\sin 4 x}{3 x}\)
Answer:
i) 1
ii)

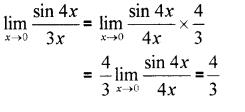
Question 10.
i) The value of \(\lim _{x \rightarrow a} \frac{x^{n}-a^{n}}{x-a}\) (MARCH-2013)
ii) Evaluate \lim _{x \rightarrow 1} \frac{x^{15}-1}{x^{10}-1}
Answer:

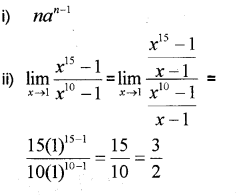
Question 11.
Find the derivative of f(x) = sin x from the first principle. (MARCH-2013)
Answer:

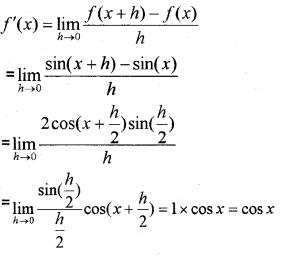
Question 12.
Find the derivative of \(\frac{x+\cos x}{\tan x}\) (MARCH-2014)
Answer:

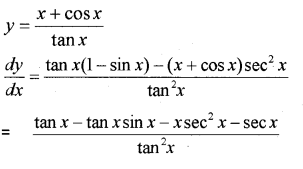
Question 13.
Find the derivatives of f(x) = sinx using the first principle. (MARCH-2014)
Answer:

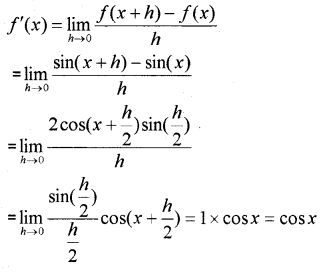
Question 14.
Find the derivative of \(\frac{x^{5}-\cos x}{\sin x}\) using the quotient rule. (MARCH-2014)
Answer:

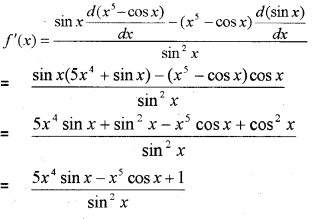
Question 15.
Using the first principle, find the derivative of cosx . (IMP-2011)
Answer:

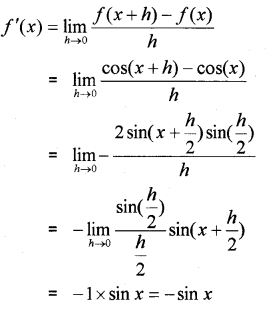
Question 16.
Find the derivative of \(\frac{\cos x}{2 x+3}\) (IMP-2012)
Answer:

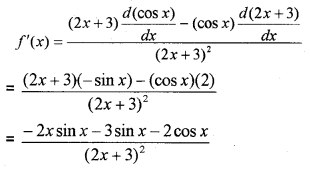
Plus One Maths Limits and Derivatives 4 Marks Important Questions

Question 1.
Evaluate (MARCH-2010)

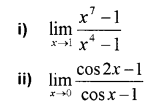
Answer:

Question 2.
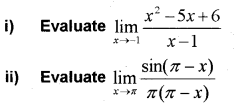(MARCH-2011)
Answer:

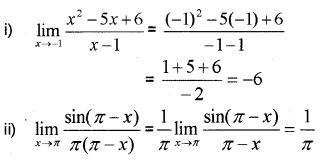
Question 3.
Compute the derivative of sec x with respect to x from first principle. (IMP-2010)
Answer:

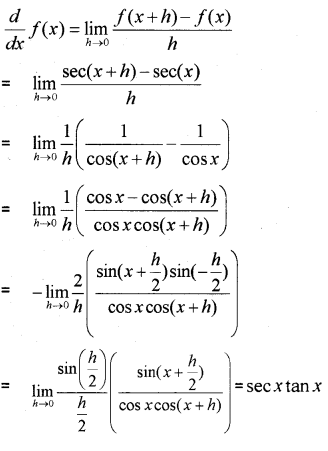
Question 4.
Find \(\lim _{x \rightarrow 2} \frac{x^{4}-4 x^{2}}{x^{2}-4}\) (IMP-2011)
ii) If y = sin 2x .Prove that \(\frac{d y}{d x}=\) = 2cos2x
Answer:

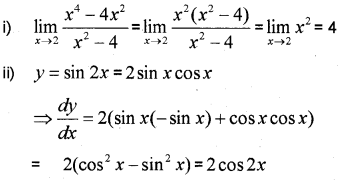
Question 5.

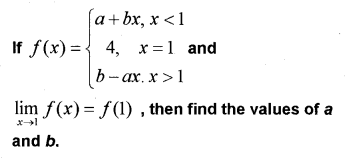
(IMP-2011)
Answer:

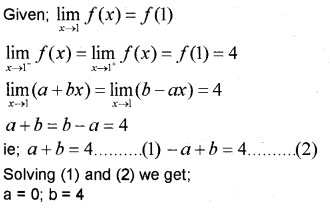
Question 6.
Find the derivative of y = cosec x from first principle. (IMP-2012)
Answer:

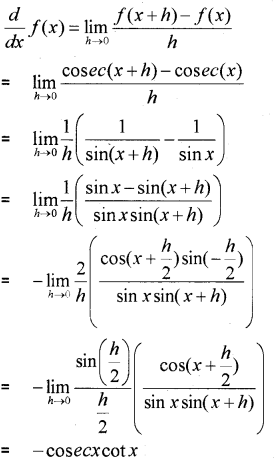
Question 7.
Find the derivative of y = cosec x from first principle. (IMP-2012)
Answer:

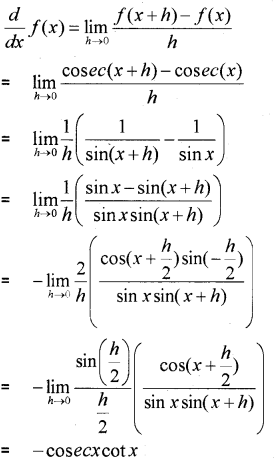
Question 8.
Find the derivative of \(\frac{x+1}{x-1}\) from first principle (IMP-2013)
Answer:

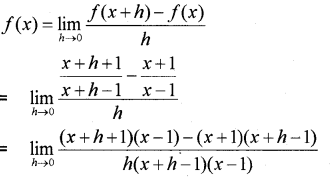
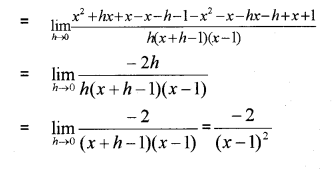
Question 9.
i) The value of \(\lim _{x \rightarrow 0} \frac{\sin 5 x}{5 x}\) (MARCH-2014)
ii) Evaluate \(\lim _{x \rightarrow 0} \frac{\sin a x}{\sin b x}, a, b \neq 0\)
Answer:
i) 1
ii)

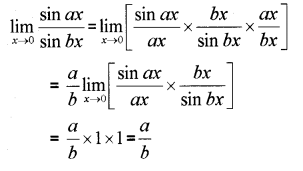
Plus One Maths Limits and Derivatives 6 Marks Important Questions

Question 1.
Find the derivative of \(\frac{1}{x}\) from first principle. (IMP-2010)
Find the derivative of
(ax + b)ⁿ (ax + c)^m
Answer:

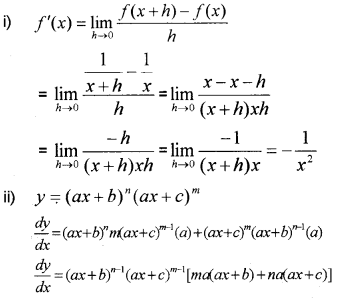
Question 2.
i) Find \(\lim _{x \rightarrow-2} \frac{x^{2}+5 x+6}{x^{2}+3 x+2}\) (IMP-2011)
ii) Find f ‘(x) given f(x) = \(\frac{x^{2}+5 x+6}{x^{2}+3 x+2}\)
Answer:

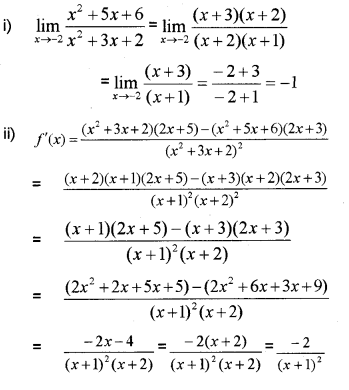
Question 3.
i) Evaluate \(\lim _{x \rightarrow 3}\left(\frac{x^{3}-27}{x^{2}-9}\right)\) (MARCH-2012)
ii) Evaluate \(\lim _{x \rightarrow 0} \frac{\tan x-\sin x}{\sin ^{3} x}\)
Answer:

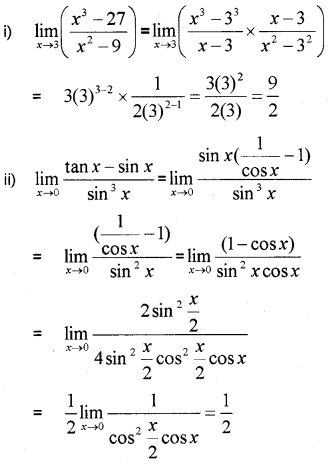
Question 4.
i) Evaluate \(\lim _{x \rightarrow 0} \frac{\sin 5 x}{\sin 3 x}\) (MARCH-2013)
ii) Find the derivate of y = cosx from the first principle.
Answer:
i)

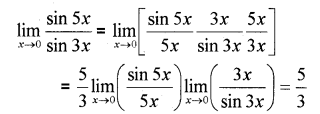
ii)

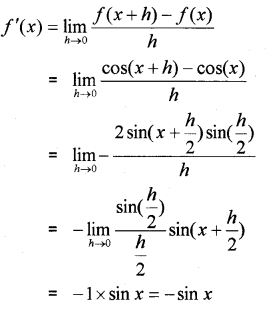
Question 5.
i) Find the derivative of \(\frac{\sin x}{x+\cos x}\) (MARCH-2014)
ii) Match the following:

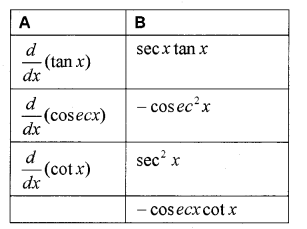
Answer:

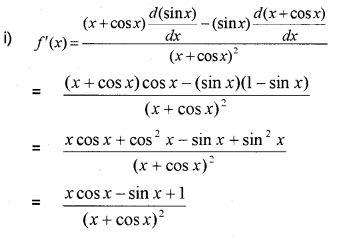
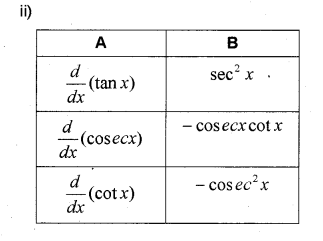
Question 6.
i) \(\frac{d}{d x}(\tan x)\) = ……… (IMP-2014)
ii) Find the derivative of 3 tan x + 5 sec x
iii) Find the derivative of /(x) = (x² + 1)sinx
Answer:

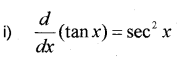
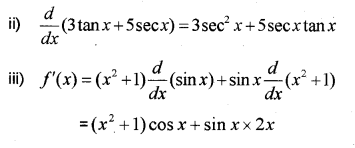
Question 7.
i) Match the following (MARCH-2015)

ii) Find the derivative of tanx using first principle.
Answer:

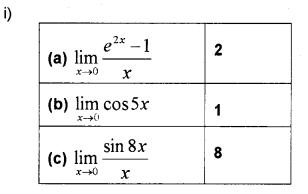
Question 8.
i) Match the following: (MARCH-2015)

ii)

Answer:

Question 9.

iii) Using first principles, find the derivative of cos x. (IMP-2015)
Answer:

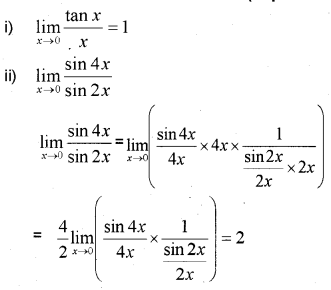
iii)

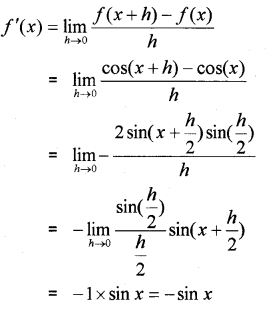
Question 10.
i) Derivative of x² – 2 at x = 10 is (IMP-2016)
a) 10
b) 20
c) -10
d) -20

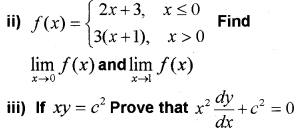
Answer:

Question 11.
i) \(\frac{d}{d x}\left(\frac{x^{n}}{n}\right)\) = ………… (MARCH-2016)
ii) Differentiate \(y=\frac{\sin x}{x+1}\) with respect to x
iii) Use first principles, find the derivative of cosx.
Answer:

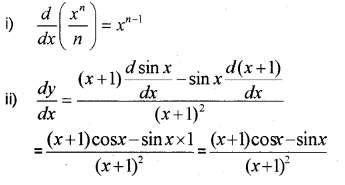
iii)

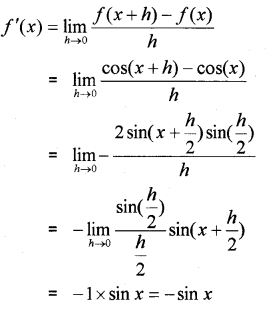
Question 12.
i) \(\frac{d}{d x}(-\sin x)\) = ………….. (MARCH-2016)
ii) Find\(\frac{d y}{d x}\) if \(y=\frac{a}{x^{4}}-\frac{b}{x^{2}}+\cos x\) where a, b are constants.
iii) Using first principles, find the derivative of sinx.
Answer:

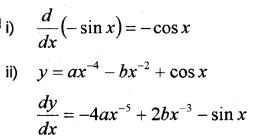
iii)

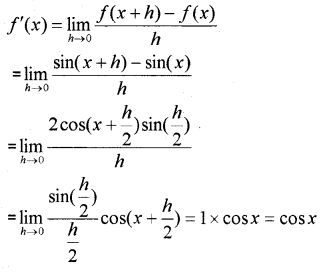
Question 14.

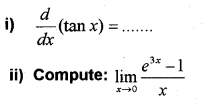
iii) Using the first principle, find the derivative of cosx (MAY-2017)
Answer:

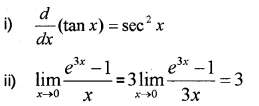
iii)

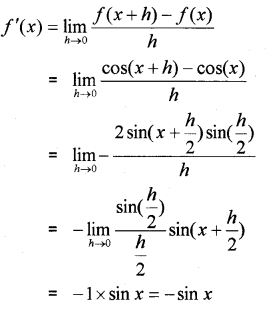
Question 15.

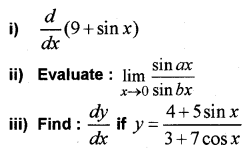
(MARCH-2017)
Answer:
i) cos x
ii)

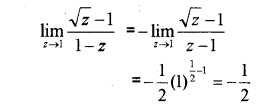
iii)

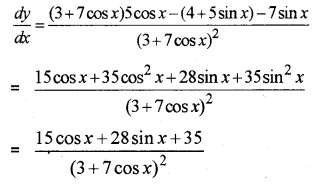
Question 16.
i) \(\lim _{x \rightarrow 0} \frac{e^{\sin x}-1}{x}=\) …….(MARCH-2017)
a) 0
b) 1
c) 2
d) 3
ii) Find
\(\lim _{x \rightarrow 0} \frac{\sqrt{1+x}-1}{x}\)
iii) Find the derivative of f(x) = sin x by using first principal.
Answer:
i) b) 1
ii)

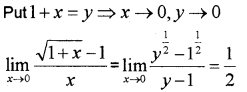
iii)

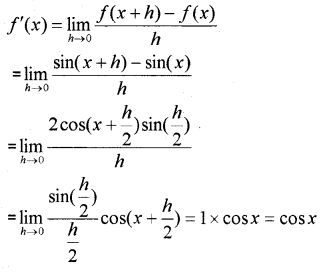
Plus One Maths Chapter Wise Previous Questions and Answer