Kerala Plus One Maths Chapter Wise Previous Questions Chapter 11 Conic Sections
Plus One Maths Conic Sections 3 Marks Important Questions
Question 1.
1. Find the equation of the Hyperbola where foci (0,±8)are and the length of the latus rectum is 24.(IMP-2012)
Answer:
Since foci (0,±8)
=> ae = 8
Latus rectum = 24= \frac {2b² }{ a }
=> 12a = b²
b² =a²(e² -1)
=> b² – a²e² -a²
=>12a = 64 – a²
=>a²+12a-64 = 0
=> a = – 16,4
acceptable value is => a = 4
=> 48 = b²
Hence equation is
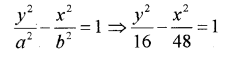
Question 2.
Find the equation of the circle with centre (- a,- b)and radius \sqrt{a^{2}+b^{2}} . (IMP-2012)
Answer:
We have the equation of a circle as;
(x-h)² + (y-k)² – r²
=> (x + a)² +(y + b)² = a² + b²
=> x² +2 ax + a² + y² +2 by + b² =a² +b²
=> x² +2ax + y² +2by = 0
Question 3.
Find the coordinate of the foci, the length of the major axis, minor axis, latus rectum and eccentricity of the ellipse \frac{x^{2}}{25}+\frac{y^{2}}{9}=1 . (MARCH-2013)
Answer:
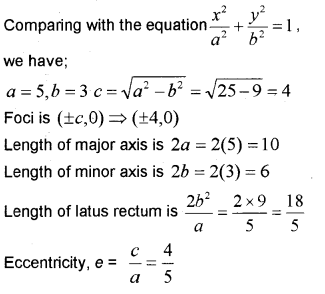
Question 4.
Consider the parabola y² =12x. (MARCH-2015)
i) Find the coordinate of the focus.
ii) Find the length of the latus rectum.
Answer:
i) Given; y² =12x comparing with y² = 4ax We have 4a = 12 => a = 3 Then; Focus is (3,0)
ii) Length of latus rectum = 4a = 12
Question 5.
Find the foci, vertices, the eccentricity and the length of the latus rectum of the hyperbola 16x² – 9y² =144. (SAY-2017)
Answer:
The equation of the hyperbola is of the form
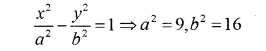
=>a² =9,b² =16
=>c² = a² +b² =9 + 16 = 25
=>c = 5
Coordinate of foci are (±5,0)
Coordinate of vertices are (±a,0) => (±3,0)
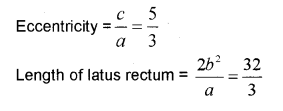
Question 6.
Directrix of the parabola x² = – 4ay is ……….. (MARCH-2014)
a) x + a = 0
b) x – a = 0
c) y – a = 0
d) y + a = 0
Find the equation of the ellipse whose length of the major axis is 20 and foci are (0 ±5)
(March-2015)
Answer:
i) y-a = 0
ii) The equation of the ellipse is of the form;
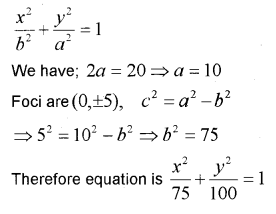
Question 7.
Find the coordinates of the focii, vertices, eccentricity and the length of the Latus Rectum of the ellipse 100x² + 25y² = 2500 (IMP-2015)
Answer:
Given: 100x² +25y² = 2500

Question 8.
Find the foci, vertices, length of the major axis and eccentricity of the ellipse: \frac{x^{2}}{25}+\frac{y^{2}}{9}=1 (MARCH-2016)
Answer:
Since 25 > 9 the standard equation of the ellipse is \frac{x^{2}}{25}+\frac{y^{2}}{9}=1 => a² =25;b² =9
c² =a² – b² =25 – 9 = 16
=>c = 4
Coordinate of foci are (±4,0)
Coordinate of vertex are (±5,0)
Length of major axis = 2a = 2 x 5 = 10
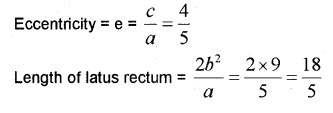
Plus One Maths Conic Sections 4 Marks Important Questions
Question 1.
An ellipse whose major axis as x-axis and the centre (0,0) passes through (4,3) and (- 1,4). (MARCH-2010)
i) Find the equation of the ellipse.
ii) Find is eccentricity.
Answer:
i)

ii)
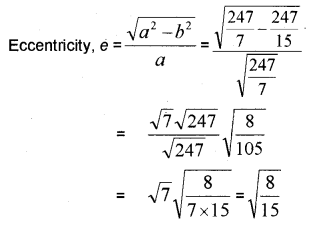
Question 2.
Consider the conic find 9y² -4x² = 36 (IMP-2010)
i) The foci.
ii) Eccentricity.
iii) Length of latus rectum.
Answer:
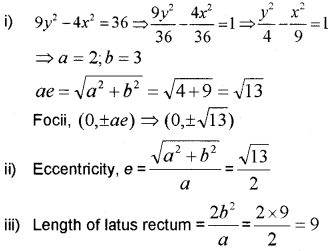
Question 3.
Find the equation of the circle with center (2,2) and passing through the point (4,5). (MARCH-2011)
Find the eccentricity and the length of latus rectum of the ellipse 4x² + 9y² =36
Answer:

Question 4.
For the hyperbola 9x² – 16y² =144 (IMP-2011)
i) find eccentricity.
ii) find the latus rectum.
Answer:
i)
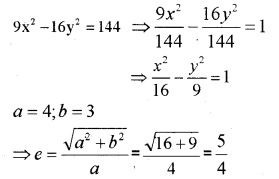
ii)
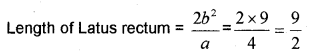
Question 5.
A hyperbola whose transverse axis is x-axis, centre (0,0) and foci (±√10,0) passes through the point (3,2) (MARCH-2012)
i) Find the equation of the hyperbola.
ii) Find the eccentricity.
Answer:
i)
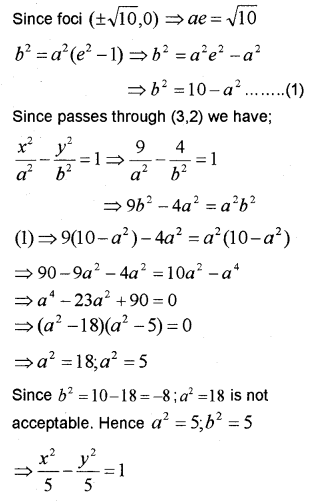
ii)
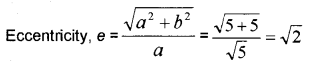
Question 6.
Find the centre and radius of the circle. (IMP-2013)
x² +y² – 8x + 10y – 12 = 0.
ii) Determine the eccentricity and length of latus rectum of the hyperbola —–
Answer:
i) Comparing with the general equation we have
g = – 4; f = 5; c = – 12
Centre – (- g,- f) => (4,- 5)
\sqrt{g^{2}+f^{2}-c} = \sqrt{16+25+12}=\sqrt{53}
ii)
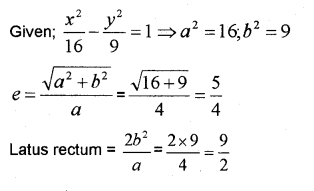
Question 7.
Consider the ellipse \frac{x^{2}}{25}+\frac{y^{2}}{9}=1. Find the coordinate of the foci, the length of the major axis, the length of the minor axis, latus rectum and eccentricity. (MARCH-2014)
Answer:
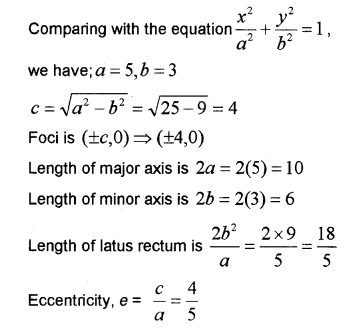
Question 8.
Which one of the following equations (IMP-2014)
represents a parabola which is symmetrical about the positive Y-axis?
a) y² = 4x
b) y² = – 8x
c) x² + 4y = 0
d) x² – 4y = 0
ii) Find the equation of the ellipse vertices are (±13,0) and foci are (±5,0)
Answer:
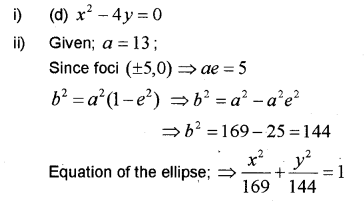
Question 9.
Match the following. (IMP-2014)

Answer:

Question 10.
i) Find the equation of the parabola with focus (6,0) and equation of the directrix is x = – 6. (MARCH-2017)
ii) Find the coordinate of the foci, vertices, the length of transverse axis, conjugate axis and eccentricity of the hyperbola \frac{x^{2}}{16}-\frac{y^{2}}{9}=1
(MARCH -2017)
Answer:

