Kerala Plus One Economics Notes Chapter 15 Measures of Central Tendency
Measures of Central Tendency
The measuring of central tendency is a way of summarizing the data in the form of a typical or representative value. There are several statistical measures of central tendency or “averages”.
The three most commonly used averages are:
- Arithmetic Mean
- Median
- Mode
Arithmetic Mean
The arithmetic mean is the most commonly used measure of central tendency. It is defined as the sum of the values of all observations divided by the number of observations and is usually denoted by x. In general, if there are N observations as x1, x2, x3,……, xN, then the Arithmetic Mean is given by
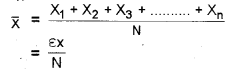
Individual Series
In individual series, values of the variables are given individually without any group, classes, or frequency.
In this case, as stated above, finding the arithmetic mean is to add all the individual values and then divide the sum by the total number of observations and is known as the direct method.
Discrete Series
Here, the data are in the grouped form, and frequency for each observation is given. But it is not in the form of classes. Here also we use a direct method or assumed mean method or step deviation method to find the arithmetic mean. If a particular method is not insisted, you can follow any method which is suitable for the problem.
In this method, mean \(\bar{x}=\frac{\varepsilon f x}{N}\)
Continuous Series: In continuous series, data are given in frequency classes. The mid-value (m) of the class has to be found out first.
Mean \(\bar{x}=\frac{\varepsilon f x}{N}\)
Median
Median is that positional value of the variable which divides the distribution into two equal parts, one part comprises all values greater than or equal to the median value and the other comprises all values less than or equal to it. The Median is the “middle” element when the data set is arranged in order of magnitude.
Individual Series: For finding the median of an individual series, first arrange it in ascending or descending order and then locate the middlemost item. Value of the middlemost item will be the median.
Median = value of \(\left(\frac{N+1}{2}\right)\)th item
Discrete Series: In discrete series items are grouped and frequencies are given. There will not be any classes. For finding the median of a discrete series, first, we arrange the items in ascending or descending order as before. Then, we find less than cumulative frequencies. Now, it is easy to locate the value of \(\left(\frac{N+1}{2}\right)\)th item.
Continuous Series: In Continuous series, data is given in frequency classes. For finding the median, first, we identify the median class. Median class is the class in which the value corresponding to the frequency (N/2)th item may lie. After identifying the median class, we use the following formula for finding the median:
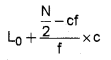
Where,
L = lower limit of the median class
N = total frequency
cf = cumulative frequency of the class preceding the median class
f = frequency of the median class
c = class width of the median class
Mode
Mode is the value around which there is the greatest concentration of values. In other words, it is the item having the largest frequency. In some cases, there may be more than one point of concentration of values and the series may be bi-modal or multi-modal. When one value occurs more frequently than any other value, the distribution is called uni-modal.
The word mode is derived from the French word ‘la mode’ which means fashion or the most popular phenomenon. The mode is thus the most popular item of a series around which there is the highest frequency density. It is denoted by Mo.
1. Individual Series: Comparing to mean and median, computation of mode is easy. In individual series, the model is that value which repeats the highest number of times. It is often found by mere inspection.
2. Discrete Series: In discrete series, the mode is determined just by inspection. The item having the highest frequency is taken as the mode.
3. Continuous Series: In continuous series, mode lies in the class having the highest frequency. Hence the modal class may be determined either by inspection or by grouping table. Then mode is determined using the formula:
![]()
where,
L0 = lower limit of the modal class
D1 = difference between the frequencies of the modal class and the class preceding it (ignoring the sign)
D2 = difference between the frequencies of the modal class and the class succeeding it (ignoring the sign); and
c = class interval of the modal class
Quartiles
Quartiles are the measures that divide the data into four equal parts; each portion contains an equal number of observations. Thus, there are three quartiles. The first Quartile (denoted by Q1) or lower quartile has 25% of the items of the distribution below it and 75% of the items are greater than it. The second Quartile (denoted by Q2) or median has 50% of items below it and 50% of the observations above it. The third Quartile (denoted by Q3) or upper Quartile has 75% of the items of the distribution below it and 25%of the items above it. Thus, Q1 and Q3 denote the two limits within which central 50% of the data lies.
