Plus One Chemistry Notes Chapter 7 Equilibrium

Kerala Plus One Chemistry Notes Chapter 7 Chemical Equilibrium

Introduction
Chemical equilibria are very important in numerous biological and environmental processes. At equilibrium state, the rate of product formed is equal to the rate of reactants formed. The mixture of reactants and products at equilibrium state is called an equilibrium mixture. A equilibrium mixture involving ions in aqueous solutions which is called as ionic equilibrium

Equilibrium In Physical Processes
Phase transformation processes are the familiar example for equilibrium in Physical process.
They are,
Solid \(\rightleftharpoons \) liquid
Liquid \(\rightleftharpoons \) gas
Solid \(\rightleftharpoons \) gas

Solid Liquid Equilibrium
Consider a perfectly insulated thermos flask containing some ice and water at 273 K and normal atmospheric pressure. Since the flask is insulated, there will be no exchange of heat between its contents and the surroundings. It is seen that as long as the temperature remains constant, there is no change in the mass of ice and water. This represents an equilibrium state between ice and water and maybe represented as

We observe there is no change in mass of both ice and water. Since the rate of both reactions are equal.
rate of melting = rate of freezing For any pure substance at 1 atmospheric pressure the temperature at which the solid and liquid phases are at equilibrium is called the normal melting point or normal freezing point of the substance.

Liquid – Vapour Equilibrium
In order to understand the liquid-vapour equilibrium, let us consider evaporation of water in a closed vessel. Consider a closed vessel connected to a manometer. The water vapour present in the vessel is first removed by placing some drying agent such as anhydrous calcium chloride in it for some time. The drying agent is then removed. Now the level of mercury in both the limbs of the manometer will be same. Introduce some water into the vessel and allow to stay at room temperature. Now water starts evaporating. A Pressure will gradually develop within the vessel due to the formation of water vapours. The change of pressure can be easily measured from the manometer. As evaporation continues, the pressure goes on increasing and the level of mercury in the right limb of the manometer starts rising. After some time it is observed that pressure becomes constant. This shows that the quantity of water vapour is not increasing any more, although liquid water is still present in the vessel. This indicates that a state of dynamic equilibrium has been attained between liquid water and water vapours.

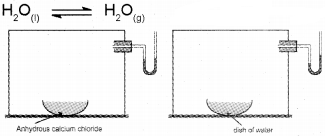
At equilibrium, both reaction take place at the same rate. Thus at equilibrium,
rate of evaporation = rate of condensation

The pressure exerted by the vapours in equilibrium with the liquid at a particular temperature is called
vapour pressure of the liquid.

It may be noted that the equilibrium between the vapours and the liquid is attained only in a closed vessel. If the vessel is open, the vapours leave the vessel and get dispersed. Hence the rate of condensation will never become equal to the rate of evapo-ration.

Solid – Vapour Equilibrium
Consider systems where solids sublime to vapour phase, For example,

Equilibrium involving Dissolution of Solid or Gas in Liquids
Solids in liquids: In a saturated solution, a dynamic equilibrium exits between the solute molecules in the solid state and in the solution: the rate of dissolution of sugar = rate of crystallisation of sugar. Gases in liquids: This equilibrium is governed by Henry’s law, which states that the mass of a gas dissolved in a given mass of a solvent at any temperature is proportional to the pressure of the gas above the solvent

General Characteristics of Equilibria involving Physical Processes
For the physical processes discussed above, following characteristics are common to the system at equilibrium:

1. Equilibrium is possible only in a closed system at a given temperature.
2. Both the opposing processes occur at the same rate and there is a dynamic but stable condition.
3. All measurable properties of the system remain constant.
4. When equilibrium is attained for a physical process, it is characterised by constant value of one of its parameters at a given temperature.
5. The magnitude of such quantities at any stage indicates the extent to which the reaction has proceeded before reaching equilibrium.

Equilibrium In Chemical Processes – Dynamic Equilibrium
Consider a general reversible reaction
A+B \(\rightleftharpoons \) C+D

Suppose the reaction is carried out in a closed container. In the beginning, the concentrations of A and B are maximum and the concentrations of C and D are minimum (equal to zero). As the reaction proceeds, the concentrations of A and B will decrease whereas the concentrations of C and D will increase. Hence the rate of the forward reaction will be high in the beginning and it will decrease gradually because of the fall in concentrations of A and B. On the other hand the velocity of the reverse reaction will be minimum at the beginning and it will increase gradually due to the increase in concentrations of C and D. Finally a stage will be reached when the rate of the forward reaction becomes equal to the rate of the reverse reaction. This state of the system is known as the state of chemical equilibrium. At this state the concentrations of the reactants and the products remain constant.

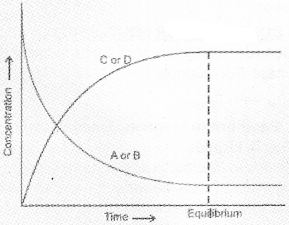
We can also start with C and D and make the reaction to proceed in the reverse direction. The concentration of C and D decreases and A and B increases. Finally, equilibrium is attained. One such example is given.
H_2(g) +l_2(g) \(\rightleftharpoons \) 2Hl_(g)

Law Of Chemical Equilibrium And Equilibrium Constant
The relation between rates of reaction and concentrations was given by Guldberg and Wage in 1864. This relation is known as law of mass action.
The relation is,
\(K_{c}=\frac{[C][D]}{[A][B]}\)
For a general reversible reaction of the type,
aA + bB \(\rightleftharpoons \) cC + dD
the equilibrium constant maybe represented as
\(K_{ c }=\frac { [c]^{ c }[D]^{ d } }{ [A]^{ a }{ \left[ B \right] }^{ b } } \)
The equation is known as the expression for the law of chemical equilibrium.

The law of chemical equilibrium or equilibrium law may thus be stated as :
At a given temperature, the product of concentrations of the reaction products raised to the respective stoichiometric coefficient in the balanced chemical equation divided by the prod-uct of concentrations of the reactants raised to their individual stoichiometric coefficients has a constant value. This is known as the Equilibrium Law or Law of Chemical Equilibrium.
If equilibrium constant for the backward reaction is
K’_c then K’_c = \(\frac{1}{K_{e}}\)

Homogeneous Equilibria
In a homogeneous system, all the reactants and products are in the same phase. For example, in the gaseous reaction,
N_2(g) + 3H_2(g) \(\rightleftharpoons \) 2NH_3(g)

Heterogeneous Equilibria
Equilibrium in a system having more than one phase
is called heterogeneous equilibrium.
For example, H₂O_(l) \(\rightleftharpoons \) H₂O_(g)

Applications Of Equilibrium Constants

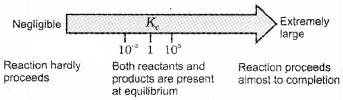
Predicting the Extent of a Reaction

• If K_c >10³, products predominate over reactants, i.e., if K_c is very large, the reaction proceeds nearly to completion.
• If K_c < 10^-3, reactants predominate over products, i.e., if K_c is very small, the reaction proceeds rarely.
• If K_c is in the range of 10^-3 to 10³, appreciable concentrations of both reactants and products are present.

Predicting The Direction Of The Reaction
The equilibrium constant is also used to find in which direction the reaction mixture of reactants and products will proceed. For this, we have to calculate the reaction quotient (Q_c) and compare with the equilibrium constant (K_c).

The concentrations of the species in Q_c are not necessarily equilibrium values.
For a general reaction aA + bB → cC + dD
\(Q_{ c }=\frac { [c]^{ c }[D]^{ d } }{ [A]^{ a }{ \left[ B \right] }^{ b } } \)
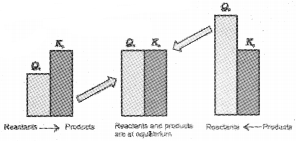
If Q_c > K_c, the reaction will proceed in the direction of the reactants (i.e., reverse reaction).
If Q_c < K_c, the reaction will proceed in the direction of the products (i.e., forward reaction).
If Q_c = K_c, the reaction mixture is already at equilibrium.

Calculating Equilibrium Concentrations
Step 1.
Write the balanced equation forthe reaction.

Step 2.
Under the balanced equation, make a table that lists foreach substance involved in the reaction:
a) the initial concentration,
b) the change in concentration on going to equilibrium, and
c) the equilibrium concentration.

In constructing the table, define x as the concentration ’ (mol/L) of one of the substances that reacts on going to equilibrium, then use the stoichiometry of the reaction to determine the concentrations of the other substances in terms of x.

Step 3.
Substitute the equilibrium concentrations into the equilibrium equation forthe reaction and solve for x. If you are to solve a quadratic equation choose the mathematical solution that makes chemical sense.

Step 4.
Calculate the equilibrium concentrations from the calculated value of x.

Step 5.
Check your results by substituting them into the equilibrium equation.

Problem
3.00 mol of PCl₅ kept in 1L closed reaction vessel was allowed to attain equilibrium at 380 K. Calculate composition of the mixture at equilibrium. K_c = 1.80

Solution
Let x mol of PCl₅ dissociated, At equilibrium:
(3 – x) x x
K_c = [PCl₃][Cl₂][PCl₅]
1.8 = x²/(3 – x)
x² + 1.8x – 5.4 = 0
x = [-1.8 ± √(1.8)² – 4(-5.4)]/2
x = [-1.8 ± √3.24 + 21.6]/2
x = [-1.8 ± 4.98]/2
x = [-1.8 + 4.98]/2
x = 1.59
[PCl₅] = 3.0 -x = 3 – 1.59 = 1.41 M
[PCl₃] = [Cl₂] = x = 1.59 M

Relationship Between Equilibrium Constant K, Reaction Quotient Q And Gibbs Energy G

• ∆G is negative, then the reaction is spontaneous and proceeds in the forward direction.
• ∆G is positive, then reaction is considered non-spontaneous. Instead, as reverse reaction would have a negative ”G, the products of the forward reaction shall be converted to the reactants.
• ∆G is O, reaction has achieved equilibrium; at this point, there is no longer any free energy left to drive the reaction.

A mathematical expression of this thermodynamic view of equilibrium can be described by the following equation:

∆G = ∆G° + RT InQ
where, G° is standard Gibbs energy.
At equilibrium, when ∆G = 0 and Q=K_c the equation becomes,
∆G = ∆G° +RTIn K = 0
∆G° = -RTInK
InK = -∆G° / RT
Therefore, K = e^∆Gv/RT

Factors Affecting Equilibria
In order to decide what course the reaction adopts and make a qualitative prediction about the effect of a change in conditions on equilibrium we use Le Chatelier’sprinciple. It states that a change in any of the factors that determine the equilibrium conditions of a system will cause the system to change in such a manner so as to reduce or to counteract the effect of the change. This is applicable to both physical and chemical equilibria.

Effect of Concentration Change
When the concentration of any of the reactants or products in a reaction at equilibrium is changed, the composition of the equilibrium mixture changes so as to minimize the effect of concentration changes.

Effect of Pressure Change
A pressure change obtained by changing the volume can affect the yield of products in case of a gaseous reaction where the total number of moles of gaseous reactants and total number of moles of gaseous products are different.

Effect of Inert Gas Addition
If the volume is kept constant and an inert gas such as argon is added which does not take part in the reaction, the equilibrium remains undisturbed. It is because the addition of an inert gas at constant volume does not change the partial pressures orthe molar concentrations of the substance involved in the reaction. So the reaction quotient does not change.

Effect of Temperature Change
Whenever an equilibrium is disturbed by a change in the concentration, pressure or volume, the composition of the equilibrium mixture changes because the reaction quotient, Q_c no longer equals the equilibrium constant, K_c However, when a change in temperature occurs, the value of equilibrium constant, K_c is changed. In general, the temperature dependence of the equilibrium constant depends on the sign of ∆H for the reaction.

• The equilibrium constant for an exothermic reaction (negative ∆H) decreases as the temperature increases.
• The equilibrium constant for an endothermic reaction (positive ∆H) increases as the temperature increases.

Temperature changes affect the equilibrium constant and rates of reactions.

Effect of a Catalyst
A catalyst increases the rate of the chemical reaction by making available a new low energy pathway for the conversion of reactants to products. It increases the rate of forward and reverse reactions that pass through the same transition state and does not affect equilibrium. Catalyst lowers the activation energy for the forward and reverse reactions by exactly ‘ the same amount.

Ionic Equilibrium In Solution
Michael Faraday classified the substances into two categories based on their ability to conduct electricity. One category of substances conduct electricity in their aqueous solutions and are called electrolytes while the other do not and are thus, referred to as non-electrolytes.

Faraday further classified electrolytes into strong and weak electrolytes.

Strong electrolytes on dissolution in water are ionized almost completely, while the weak electrolytes are only partially dissociated.

Acids. Bases And Salts

Arrhenius Concept of Acids and Bases
According to Arrhenius theory, acids are substances that dissociates in water to give hydrogen ions H⁺_(aq) and bases are substances that produce hydroxyl ions OH^–_(aq). The ionization of an acid HX _(aq) can be represented by the following equations:
HX_(aq) → H⁺(aq) + X^–(aq)
or
HX(aq) + H₂O(l) -> H₃O⁺(aq) + X^–(aq)

The Bronsted-Lowry Acids and Bases
The Danish chemist, Johannes Bronsted and the English chemist, Thomas M. Lowry gave a more general definition of acids and bases. According to Bronsted-Lowry theory, acid is a substance that is capable of donating a hydrogen ion l-T and bases are substances capable of accepting a hydrogen ion, H⁺. In short, acids are proton donors and bases are proton acceptors.

The acid-base pair that differs only by one proton is called a conjugate acid-base pair. Therefore, OH^– is called the conjugate base of an acid H₂O and NH₄⁺ is called conjugate acid of the base NH₃. If Bronsted acid is a strong acid then its conjugate base is a weak base and vice versa.
Consider the example of ionization of hydrochloric acid in water.

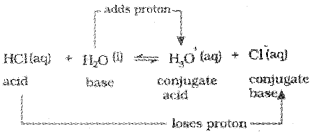
Ionization Of Acids And Bases

The Ionization constant of water and its ionic product
Water undergoes self ionisation to a small extent as follows.

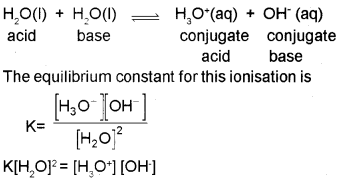
Since [H₂O] is constant, K[H₂O]² may be taken as a new constant K_w. Thus,
K_w= [H₃O⁺][OH^–]

Where K_w is called ionic product of water. Its value is 1 x10‘14 mol2 L2 at 298 K. In pure water, the concen-tration of hydronium ions and hydroxyl ions are equal. Therefore in pure water,
[H₃O⁺] = [OH^–] = 1 × 10^-7 mol L^-1

Since the ionisation of water increases with increase of temperature, K_w increases with rise of temperature.

The pH Scale
Hydronium ion concentration in molarity is more conveniently expressed on a logarithmic scale known as the pH scale.

The pH of a solution is defined as the negative logarithm to base 10 of the activity (a_H+) of hydrogen ion.
i.e., pH = – log aH^H+ = – log {[H+]/,mol L^-1}
Acidic solution has pH < 7 Basic solution has pH > 7
Neutral solution has pH = 7

Ionization Constants of Weak Acids

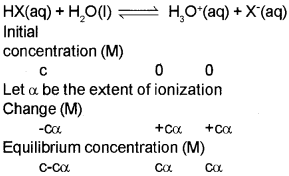
Here, c= initial concentration of the undissociated acid, HXat time, t = 0. α = extent up to which HX is ionized into ions.
K_a = c²a² / c(1 – α) = cα²/1 – A
K_a is called the dissociation or ionization constant.

Ionization of Weak Bases
The equilibrium constant for base ionization is called base ionization constant and is represented by K_b.

When equilibrium is reached, the equilibrium constant can be written as:
K_b = (cα)² / c(1 – α) = cα² / (1 – α)
considering the base-dissociation equilibrium reaction:
K_b = [BH⁺][OH^–]/[B]
Then multiplying and dividing the above expression by [H⁺], we get:
K_b = [BH⁺][OH^–][H⁺]/[B][H⁺]
= {[OH^–][H⁺]}{[BH⁺]/[B][H⁺]}
= K_w/K_a
Then we get the following relation;
pK_a + PK_b = pK_q = 14 (at 298 K)

Common ion effect in the ionization of Acids and Bases.
Common ion effect my be defined as the suppression of the dissociation of a weak electrolyte (weak acid or weak base) by the addition of some strong electrolyte containing a common ion.

Factors Affecting Acid Strength
Dissociation of an acid depends on the strength and polarity of the H-A bond.
Electronegativity of A increases CH₄ < NH₃ < H₂O < HF Acid strength increases

Common Ion Effect in the Ionization of Acids and Bases
Ka = [H⁺] [Ac^–] / [HAc] acetate ions to an acetic acid solution results in decreasing the concentration of hydrogen ions, [H⁺], Also, if H⁺ ions are added from an external source then the equilibrium moves in the direction of undissociated acetic acid. This phenomenon is an example of common ion effect.

Hydrolysis of Salts and the pH of their Solutions
Salts formed by the reactions between acids and bases in definite proportions, undergo ionization in water. The cations/anions formed on ionization of salts either exist as hydrated ions in aqueous solutions or interact with water to reform corresponding acids/bases depending upon the nature of salts. The later process of interaction between water and cations/anions or both of salts is called hydrolysis.

Buffer Solutions
The solutions which resist change in pH on dilution or with the addition of small amounts of acid or alkali are called Buffer Solutions.

Solubilityequilibriaof Sparingly Soluble Salts

Solubility Product Constant
The equilibrium between the undisolved solid and the ions in a saturated solution can be represented by the equation:

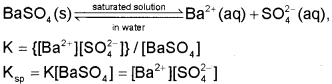
We call K_sp the solubility product constant or simply solubility product.

Thus, solubility product of a salt is the product of concentration of ions in its saturated solution, raised to a power equal to the number of times the ions occur in the equation representing the dissociation of the salt.

The term K_sp in equation is given by Q_sp when the concentration of one or more species is not the concentration under equilibrium. Obviously under equilibrium conditions K_sp = Q_sp but otherwise it gives the direction of the processes of precipitation or dissolution.

Common Ion Effect on Solubility of Ionic Salts
The solubility of salts of weak acids like phosphates increases at lower pH. This is because at lower pH the concentration of the anion decreases due to its proto-nation. This, in turn, increases the solubility of the salt so that K_sp = Q_sp.

Ncert Supplementary Syllabus

Designing Buffer Solution
Knowledge of pK_a, pK_b and equilibrium constant help us to prepare the buffer solution of known pH. Let us see how we can do this.

Preparation of Acidic Buffer
To prepare a buffer of acidic pH we use weak acid and its salt formed with strong base. We develop the equation relating the pH, the equilibrium constant, K_a of weak acid and ratio of concentration of weak acid and its conjugate
base. For the general case where the weak acid HA ionises in water,

ratio of concentration of conjugate base (anion) of the acid and the acid present in the mixture. Since acid is a weak acid, it ionises to a very little extent ‘and concentration of [HA] is negligibly different from concentration of acid taken to form buffer. Also, most of the conjugate base, [A^–], comes from the ionisation of salt of the acid. Therefore, the concentration of conjugate base will be negligibly different from the concentration of salt. Thus, equation (A-2) takes the form: pH-pK_a + log\(\frac{[\mathrm{Salt}]}{[\mathrm{Acid}]}\)

In the equation (A-1), if the concentration of [A^–] is equal to the concentration of [HA], then pH = pK_a because value of log 1 is zero. Thus if we take molar concentration of acid and salt (conjugate base) same, the pH of the buffer solution will be equal to the pK_a of the acid. So for preparing the buffer solution of the required pH we select that acid whose pK_a is close to the required pH. For acetic acid pK_a value is 4.76, therefore pH of the buffer solution formed by acetic acid and sodium acetate taken in equal molar concentration will be around 4.76.

A similar analysis of a buffer made with a weak base and its conjugate acid leads to the result,

pH of the buffer solution can be calculated by using the equation pH + pOH =14.

We know that pH + pOH = pK_w and pK_a + pK_b = pK_w On putting these values in equation (A-3) it takes the form as follows:

If molar concentration of base and its conjugate acid (cation) is same then pH of the buffer solution will be same as pK_a for the base. pK value for ammonia is 9.25; therefore a buffer of pH close to 9.25 can be obtained by taking ammonia solution and ammonium chloride solution of equal molar concentration. For a buffer solution formed by ammonium chloride and ammonium hydroxide, equation (A-4) becomes:

pH of the buffer solution is not affected by dilution because ratio under the logarithmic term remains unchanged.

Plus One Chemistry Notes