Kerala Plus One Chemistry Notes Chapter 6 Thermodynamics
Introduction
The study of energy transformations forms the subject matter or thermodynamics.
Thermodynamic Terms
The system and the surroundings
A system in thermodynamics refers to that part of universe in which observations are made and remain-ing universe constitutes the surroundings. The surroundings include everything other than the system. System and the surroundings together constitute the universe.
Types Of The System
1. Open System:
In an open system, there is exchange of energy and matter between system and surroundings
2. Closed System:
In a closed system, there is no exchange of matter, but exchange of energy is possible between system and the surroundings
3. Isolated System:
In an isolated system, there is no exchange of energy or matter between the system and the surroundings. The presence of reactants in a thermos flask or any other closed insulated vessel is an example of an isolated system.
The State Of The System
The state of a system means the condition of the system when is macroscopic properties have definite values. If any of the macroscopic properties of the system changes, the state of the system will change. A process is said to occur when the state of the system changes.
The measurable properties required to describe the state of a system are called state variables or state functions. Temperature, pressure, volume, composition etc. are state variables.
The Internal Energy as a State Function
1. Work:
The system which can’t exchange heat between the system and surroundings through its boundary is called adiabatic system. The manner in which the state of such a system may be changed will be called adiabatic process. Adiabatic process is a process in which there is no transfer of heat between the system and surroundings.
Internal energy, U, of the system is a state function. The positive sign expresses that wad is positive when work is done on the system. Similarly, if the work is done by the system, wad will be negative.
2. Heat:
A system change its internal energy by ex-change of heat. The q is positive, when heat is transferred from the surroundings to the system and q is negative when heat is transferred from system to the surroundings. first law of thermodynamics, which states that The energy of an isolated system is constant.
i. e., ∆U = q + w
It is commonly stated as the law of conservation of energy i.e., energy can neither be created nor be destroyed.
Applications
Work
The work done due to expansion or compression of a gas against an opposing external pressure is called the pressure – volume type of work. It is a kind of mechanical work.
If Y is the initial volume and Vf is the final volume of a certain amount of gas and Pex is the external pressure, then the work involved in the process is given by
w = – Pex (Vf – Vi) or w = -Pex ∆V
The negative sign of this expression is required to obtain conventional sign for w.
It must be noted that the above expression gives the work done by the gas in irreversible expansion or compression
Work done in isothermal reversible expansion (or compression) of a gas is given by the relation
wrev =-2.303 nRT log \(\frac{V_{f}}{V_{i}}\)
Where n = the number of moles of the gas
Free expansion
Expansion of a gas in vaccum is called free expansion. Since P = 0 in vacuum, work done in free expansion = 0
Isothermal and free expansion of an ideal gas.
1. For isothermal irreversible change q= -w = pex (Vf – Vi)
2. For isothermal reversible change
q = -w = nRT In \(\frac{V_{f}}{V_{i}}\)
= 2.303 nRT log \(\frac{V_{f}}{V_{i}}\)
3. For adiabatic change q = 0, ∆U = wad
Enthalpy, H
1. A useful new state function:
We know that the heat absorbed at constant volume is equal to change in the internal dnergy i.e., ∆U= qp
We may write equation as ∆U=qp – p∆V at constant pressure, where qp is heat absorbed by the system and -pAV represent expansion work done by the system.
We can rewrite the above equation as U2 -U1 = qp – p(V2 – V1)
On rearranging, we get qp = (U2 +pV2) = (U1 +pV1) Now we can define another thermodynamic function, the enthalpy H [Greek word enthalpien, to warm or heat content] as :
H=U+PV
so, equation becomes qp = H2 – H1 = ∆H
Although q is a path dependent function, H is a state function because it depends on U, p and V, all of which are state functions.
Therefore, ∆H is independent of path. Hence,qp is also independent of path.
For finite changes at constant pressure, we can write ∆H = ∆U + ∆pV
It is important to note that when heat is absorbed by the system at constant pressure, we are actually measuring changes in the enthalpy. Remember ∆H = qp heat absorbed by the system at constant pressure.
∆H is negative for exothermic reactions which evolve heat during the reaction and ∆H is positive for endothermic reactions which absorb heat from the surroundings.
2. Extensive and Intensive Properties:
An extensive property is a property whose value depends on the quantity or size of matter present, in the system. For example, mass, volume, internal energy, enthalpy, heat capacity, etc. Those properties which do not depend on the quantity or size of matter present are known as intensive properties. For example temperature, density, pressure, etc.
3. Heat Capacity:
The heat required to rise the temperature of the system in case of heat absorbed by the system.
The increase of temperature is proportional to the heat transferred q = coeff × ∆T
The magnitude of the coefficient depends on the size, composition, and nature of the system. We can also write it as q = C ∆T
The coefficient, C is called the heat capacity. Water has a large heat capacity i.e., a lot of energy is needed to raise its temperature. C is directly proportional to amount of substance. The molar heat capacity of a substance, Cm = \(\frac{C}{n}\), is the heat capacity for one mole of the substance and is the quantity of heat needed to raise the temperature of one mole by one degree Celsius (or one kelvin).
Specific heat, also called specific heat capacity is the quantity of heat required to raise the temperature of one unit mass of a substance by one degree Celsius (or one kelvin). q = c × m × ∆T
4. The relationship between Cp and Cv for an ideal gas:
At constant volume, the heat capacity, C is denoted by Cv and at constant pressure, this is denoted by Cp. Let us find the relationship between the two. We can write equation for heat, q at constant volume as qv=Cv ∆T = ∆U at constant pressure as qp = Cp∆T = ∆H
The difference between Cp and Cv can be derived for an ideal gas as:
For a mole of an ideal gas, ∆H = ∆U + ∆(pV)
= ∆U + ∆(RT)
= ∆U + R∆T
On putting the values ∆H of ∆H and we have
Cp∆T = Cv∆T
Cp = Cv +R
Cp – Cv = R
Measurement Of ∆U And ∆H: Calorimetry
We can measure energy changes associated with chemical or physical processes by an experimental technique called calorimetry.
1. ∆U measurements:
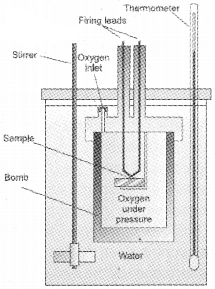
Here, a steel vessel (the bomb) is immersed in a water bath. The whole device is called calorimeter. The steel vessel is immersed in water bath to ensure that no heat is lost to the surroundings. A combustible substance is burnt in pure dioxygen supplied in the steel bomb. Heat evolved during the reaction is transferred to the water around the bomb and its temperature is monitored. Since the bomb calorimeter is sealed, its volume does not change i.e., the energy changes associated with reactions are measured at constant volume. Under these conditions, no work is done as the reaction is carried out at constant volume in the bomb calorimeter. Even for reactions involving gases, there is no work done as ∆V = 0.
2. ∆H measurements:
Measurement of heat change at constant pressure (generally under atmospheric pressure) can be done in a calorimeter at constant p
In an exothermic reaction, heat is evolved, and system loses heat to the surroundings.
Therefore, qp will be negative and ∆rH will also be negative. Similarly in an endothermic reaction, heat is absorbed, qp is positive and ∆rH will be positive.
Enthalpy Change, ∆rH Of A Reaction – Reaction Enthalpy
The enthalpy change accompanying a reaction is called the reaction enthalpy.
The reaction enthalpy change is denoted by ∆rH
∆rH = (sum of enthalpies of products) – (sum of enthalpies of reactants)
1. Standard enthalpy of reactions:
The standard enthalpy of reaction is the enthalpy change for a reaction when all the participating substances are in their standard states.
The standard state of a substance at a specified temperature is its pure form at 1 bar.
2. Enthalpy changes during phase transformations:
The enthalpy change that accompanies melting of one mole of a solid substance in standard state is called standard enthalpy of fusion or molar enthalpy of fusion ∆fusH°.
Amount of heat required to vaporize one mole of a liquid at constant temperature and under standard pressure (1bar) is called its standard enthalpy of vaporization or molar enthalpy of vaporization ∆vapH°. And that of sublimation is called Standard enthalpy of sublimation, ∆subH°.
3. Standard enthalpy of formation
The standard enthalpy change for the formation of one mole of a compound from its elements in their most stable states of aggregation (also known as reference states) is called Standard Molar Enthalpy of Formation( ∆fH°).
Hess’s Law of Constant Heat Summation Hess’s Law:
If a reaction takes place in several steps then its standard reaction enthalpy is the sum of the standard enthalpies of the intermediate reactions into which the overall reaction may be divided at the same temperature.
Enthalpies For Different Types Of Reactions
1. Standard enthalpy of combustion
Enthalpy of combustion of a substance is defined as the enthalpy change accompanying the complete combustion of one mole of the substance in excess of air or oxygen.
Standard enthalpy of combustion is defined as the enthalpy change accompanying the complete combustion of one mole of the substance in excess of air or oxygen when all the reactants and products are tin their standard states at the specified temperature. It is denoted as ∆cH°.
For example, the complete combustion of one mole of methane evolves 890.3 kJ of heat. Thus, the enthalpy of combustion of methane is- 890.3 kJ mol-1.
Combustion reactions are always accompanied by the evolution of heat. Hence enthalpy of combustion is always negative.
2. Enthalpy of atomization (symbol: ∆aH°)
It is the enthalpy change on breaking one mole of bonds completely to obtain atoms in the gas phase.
3. Bond Enthalpy (symbol: ∆bondH°)
The bond dissociation enthalpy is the change in enthalpy when one mole of covalent bonds of a gaseous covalent compound is broken to form products in the gas phase.
Lattice Enthalpy
The lattice enthalpy of an ionic compound is the enthalpy change which occurs when one mole of an ionic compound dissociates into its ions in gaseous state.
Spontaneity
A process which has an urge or a natural tendency to occur under a given set of conditions is known as a spontaneous process.
Some of the spontaneous process need no initiation, i.e., they take place by themselves. Dissolution of common salt in water, evaporation of water in an open vessel, combination of NO and oxygen to form NO2, neutralisation reaction between NaOH and HCl, etc. are examples of such processes. But some other spontaneous processes need initiation. For example, hydrogen reacts with oxygen to form water only when initiated by passing an electric spark. Once initiated, it occurs by itself.
1. Is decrease in enthalpy a criterion for spontaneity?
By analogy, we may be tempted to state that a chemical reaction is spontaneous in a given direction, because decrease in energy has taken place, as in the case of exothermic reactions.lt becomes obvious that while decrease in enthalpy may be a contributory factor for spontaneity, but it is not true for all cases.
2. Entropy and spontaneity
Entropy(S) is the measure of the degree of randomness or disorder in the system. The greater the disorder in an isolated system, the higher is the entropy. The crystalline solid state is the state of lowest entropy (most ordered), The gaseous state is state of highest entropy. ∆S is independent of path.
∆S is related with q and T for a reversible reaction as: ∆S = \(\frac{q_{\text {rev }}}{T}\)
When a system is in equilibrium, the entropy is maximum, and the change in entropy, ∆S = 0.
3. Gibbs energy and spontaneity
we define a new thermodynamic function the Gibbs energy or Gibbs function, G, as G = H – TS
Gibbs energy change is a better parameter to determine the spontaneity or feasibility of a process. It can be summarised as follows.
i) If ∆G is negative (i.e., <0) the precess will be spontaneous. ii) If ∆G is zero, the precess is in equilibrium state. iii) If ∆G is positive (i.e., >0), the process is non- spontaneous in the forward direction. The reverse process may be spontaneous.
Ncert Supplementary Syllabus
Enthalpy of Dilution
It is known that enthalpy of solution is the enthalpy change associated with the addition of a specified amount of solute to the specified amount of solvent at a constant temperature and pressure. This argument can be applied to any solvent with slight modification. Enthalpy change for dissolving one mole of gaseous hydrogen chloride in 10 mol of water can be represented by the following equation.
HCl(g) + 10 aq. → HCl. 10 aq. ∆H = -69.01 kJ/mol
Let us consider the following set of enthalpy changes:
(S- 5) HCl(g) + 25 aq. → HCl.25 aq. ∆H = -72.03 kJ/mol
(S-2) HCtlgi + 40 aq. → HCl.40 aq. ∆H = -72.79 kJ/mol
(S-3) HCl(g) + ∞ aq. → HCl. ∞aq. ∆H = -74.85 kJ/mol
The values of ∆H show general dependence of the enthalpy of solution on amount of solvent. As more and more solvent is used, the enthalpy of solution approaches a limiting value, i.e, the value in infinitely dilute solution. For hydrochloric acid this value of AH is given above in equation (S-3).
If we subtract the first equation (equation S-1) from the second equation (equation S-2) in the above set of equations, we obtain
This value (-0.76kJ/mol) of ∆H is enthalpy of dilution. It is the heat withdrawn from the
HCl.25 aq. + 15 aq. → HCl.40 aq.
∆H = [ -72.79 – (-72.03)] kJ/mol
= -0.76 kJ/mol
This value (-0.76kJ/mol) of ∆H is enthalpy of dilution. It is the heat withdrawn from the surroundings when additional solvent is added to the solution. The enthalpy of dilution of a solution is dependent on the original concentration of the solution and the amount of solvent added.
Entropy and Second Law of Thermodynamics
We know that for an isolated system the change in energy remains constant. Therefore, increase in entropy in such systems is the natural direction of a spontaneous change. This, in fact, is the second law of thermodynamics. Like first law of thermodynamics, second law can also be stated in several ways. The second law of thermodynamics explains why spontaneous exothermic reactions are so common. In exothermic reactions, heat released by the reaction increases the disorder of the surroundings and overall entropy change is positive which makes the reaction spontaneous.
Absolute Entropy and Third Law of Thermodynamics
Molecules of a substance may move in a straight line in any direction, they may spin like a top and the bonds in the molecules may stretch and compress. These motions of the molecule are called translational, rotational and vibrational motion respectively. When temperature of the system rises, these motions become more vigorous and entropy increases. On the other hand, when temperature is lowered, the entropy decreases. The entropy of any pure crystalline substance approaches zero as the temperature approaches absolute zero. This is called third law of thermodynamics. This is so because there is perfect order in a crystal at absolute zero.
The statement is confined to pure crystalline solids because theoretical arguments and practical evidences have shown that entropy of solutions and super cooled liquids is not zero at 0 K. The importance of the third law lies in the fact that it permits the calculation of absolute values of entropy of pure substance from thermal data alone. For a pure substance, this can be done by summing \(\frac{q_{\text {rev }}}{T}\) increments from 0 K to 298 K. Standard entropies can be used to calculate standard entropy changes by a Hess’s law type of calculation.
