Plus One Chemistry Notes Chapter 2 Structure of Atom

Kerala Plus One Chemistry Notes Chapter 2 Structure of Atom

Introduction
The atomic theory of matter was first proposed by John Dalton. His theory, called Dalton’s atomic theory, regarded the atom as the ultimate particle of matter.

Sub-Atomic Particles
Discovery Of Electron
The experiments of Michael Faraday in discharge tubes showed that when a high potential is applied to a gas taken in the discharge tube at very low pres-sures, certain rays are emitted from the cathode. These rays were called cathode rays.

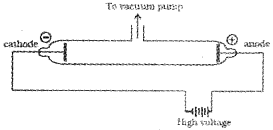
The results of these experiments are summarised below:
1. The cathode rays start from cathode and move towards the anode.

2. In the absence of electrical or magnetic field, these rays travel in straight lines.ln the presence of electrical or magnetic field, they behave as negatively charged particles, i.e.,they consist of negatively charged particles, called electrons.

3. The characteristics of cathode rays (electrons) do not depend upon the material of electrodes and the nature of the gas present in the cathode ray tube.Thus, we can conclude that electrons are the basic constituent of all the atoms.

Charge To Mass Ratio Of Electron
In 1897, the British physicist J.J. Thomson measured the ratio of electrical charge (e) to the mass of electron (m_e) by using cathode ray tube and applying electrical and magnetic field perpendicular to each other as well as to the path of electrons.

From the amount of deviation of the particles from their path in the presence of electrical or magnetic field, the value of e/m was found to be 1.75882 × 10¹¹ coulomb per kg or approximately 1.75288 × 10⁸ cou-lomb per gram. The ratio e/m was found to be same irrespective of the nature of the gas taken in the dis-charge tube and the material used as the cathode.

Charge Of The Electron
Millikan (1868-1953) devised a method known as Oil drop experiment (1906-14), to determine the charge on the electrons. He found the charge on the electron to be – 1.6 × 10-¹⁹C.

Mass of the electron (m)

Discovery Of Protons And Neutrons
Electrical discharge earned out in the modified cathode ray tube led to the discovery of canal rays. The characteristics of these positively charged particles are listed below:

• unlike cathode rays, the e/m ratio of the particles depend upon the nature of gas present in the cathode ray tube.
• Some of the positively charged particles carry a multiple of the fundamental unit of electrical charge.
• The behaviour of these particles in the magnetic or electrical field is opposite to that observed for cathode rays.

The smallest and lightest positive ion was obtained from hydrogen and was called proton. Later, electrically neutral particles were discovered by Chadwick (1932) by bombarding a thin sheet of beryllium by α – particles when electrically neutral particles having a mass slightly greater than that of the protons was emitted. He named these particles as neutrons.

Atomic Models

Thomson Model Of Atom
J.J. Thomson was the first to propose a model of the atom. According to him, the atom is a sphere in which positive charge is spread uniformly and the electrons are embedded in it so as to make the atom electrically neutral. This model is also known as “plumpudding model’. But this model was soon discarded as it could not explain many of the experimental observations.

Rutherford’s Nuclear Model of Atom
Rutherford and his students (Hans Geiger and Ernest Marsden) bombarded very thin gold foil with α – particles. The experiment is known as α -particle scattering experiment. On the basis of the observations, Rutherford drew the following conclusions regarding the structure of atom :

1. Most of the space in the atom is empty as most of the α -particles passed through the foil undeflected.

2. A few α – particles were deflected. Since the α – particles are positively charged, the deflection must be due to enormous repulsive force showing that the positive charge of the atom is not spread throughout the atom as Thomson had presumed. The positive charge has to be concentrated in a very small volume that repelled and deflected the positively charged α – particles.

3. Calculations by Rutherford showed that the volume occupied by the nucleus is negligibly small as compared to the total volume of the atom.

On the basis of above observations and conclusions, Rutherford proposed the nuclear model of atom (after the discovery of protons). According to this model:
1.The positive charge and most of the mass of the atom was densely concentrated in extremely small region. This very small portion of the atom was called nucleus by Rutherford.

2. The electrons move around the nucleus with a very high speed in circular paths called orbits. Thus, Rutherford’s model of atom resembles the solar system in which the nucleus plays the role of sun and the electrons that of revolving planets.

3. Electrons and the nucleus are held together by electrostatic forces of attraction.

Atomic Numberand Mass Number
’ Knowing the atomic number Z and mass number A of an element, we can calculate the number of protons, electrons and neutrons present in the atom of the element.
Atomic Number (Z) = Number of protons = Number of electrons
Mass Number (A) – Atomic number (Z) = Number of neutrons

Isotopes, Isobars And Isotones
Isotopes are atoms of the same element having the same atomic number but different mass numbers. They contain different number of neutrons. For ex-ample, there are three isotopes of hydrogen having mass numbers 1,2 and 3 respectively. All the three isotopes have atomic number 1. They are represented as \(_{ 1 }^{ 1 }{ H }\), \(_{ 1 }^{ 2 }{ H }\) and \(_{ 1 }^{ 3 }{ H }\) and named as hydrogen or protium, deuterium (D) and tritium (T) respectively. Isobars are atoms of different elements which have the same mass number. For example, \(_{ 6 }^{ 14 }{ C }\) and \(_{ 7 }^{ 14 }{ N }\) are isobars.
Isotones may be defined as atoms of different elements containing same number of neutrons. For example \(_{ 6 }^{ 13 }{ C }\) and \(_{ 7 }^{ 14 }{ N }\) are isotones.

Developments Leading To The Bohr’S Model Of Atom
Neils Bohr improved the model proposed by Rutherford. Two developments played a major role in the formulation of Bohr’s model of atom. These were:

1. electromagnetic radiation possess both wave like and particle like properties(Dual character)
2. Experimental results regarding atomic spectra which can be explained only by assuming quantized electronic energy levels in atoms.

Wave Nature Of Electromagnetic Ra-Diation
Light is the form of radiation and it was supposed to be made of particles known as corpuscules.
As we know, waves are characterised by wavelength (λ), frequency (υ) and velocity of propagation (c) and these are related by the equation
c = vλ or v = \(\frac { c }{ \lambda } \)

The wavelengths of various electromagnetic radiations increase in the order.
γ rays < X-rays< uv rays < visible < IR < Microwaves < Radio waves

Particle Nature Of Electro Magnetic Radiation: Planck’S Quantum Theory
Planck suggested that atoms and molecules could emit (or absorb) energy only in discrete quantities and not in a continuous manner, a belief popular at that time. Planck gave the name quantum to the smallest quantity of energy that can be emitted or absorbed in the form of electromagnetic radiation. The energy (E) of a quantum of radiation is proportional to its frequency (υ) and is expressed by the equation E = hυ

Photoelectric Effect
When metal was exposed to a beam of light, electrons were emitted. This phenomenon is called photoelectric effect. Obseravations of the photoelectric effect experiment are the following:

• There is no time lag between the striking of light beam and the ejection of electrons from the metal surface.
• The number of electrons ejected is proportional to the intensity or brightness of light.
• For each metal, there is a characteristic minimum frequency, u₀ (also known as threshold frequency) below which photoelectric effect is not observed. At a frequency u>u₀, the ejected electrons come out with certain kinetic energy.

The kinetic energies of these electrons increase with the increase of frequency of the light used.

Using Plank’s quantum theory Einstein explained photoelectric effect. When a light particle, photon with sufficient energy strikes an electron instantaneously to the electron during the collision and the electron is ejected without any time lag. Greater the energy of photon greater will be the kinetic energy of ejected electron and greater will be the frequency of radiation.

If minimum energy to eject an electron is hv0 and the photon has an energy equal to hv. Then kinetic en-ergy of photoelectron is given by, hv=hv₀ + 1/2 m_ev² where m_e is the mass of electron and hv₀ is called the work function.

Duel Behaviour Of Electromagnetic Ra-Diation
Light has dual behaviour that is it behaves either as a wave or as a particle. Due to this wave nature, it shows the phenomena of interference and diffraction.

Evidence For The Quantized Electronic Energy Levels : Atomic Spectra
It is observed that when a ray of white light is passed through a prism, the wave with shorter wavelength bends more than the one with a longer wavelength. Since ordinary white light consists of waves with ail the wave-lengths in the visible range, a ray of white light is spread out into a series of coloured bands called spectrum. In a continuous spectrum light of different colours merges together. For example violet merges into blue, blue into green and soon.

Emission and absorption spectra
The spectrum of radiation emitted by a substance that has absorbed energy is called an emission spectrum. Atoms, molecules or ions that have absorbed radiation are said to be “excited”.

A continuum of radiation is passed through a sample which absorbs radiation of certain wavelengths. The missing wavelength which corresponds to the radiation absorbed by the matter, leave dark spaces in the bright continuous spectrum. The study of emission or absorption spectra is referred to as spectroscopy Line spectra or atomic spectra is the spectra where emitted radiation is identified by the appearance of bright lines in the spectra.

Line spectrum of Hydrogen
The hydrogen spectrum consists of several series of lines named after their discoverers. Balmershowed in 1885 on the basis of experimental observations that if spectral lines are expressed in terms of wavenumber (\(\overline { v } \)), then the visible lines of the hydrogen spectrum obey the following formula :
\(\overline { v } \) = 109,677 \(\left[\frac{1}{2^{2}}-\frac{1}{n^{2}}\right] \mathrm{cm}^{-1}\)
where n = 3, 4, 5, ………….
The series of lines described by this formula are called the Balmer series.

The value 109,677cm^-1 is called the Rydberg constant for hydrogen. The first 5 series of lines correspond to n₁ = 1, 2, 3, 4, 5 are known as Lyman, Balmer, Paschen, Bracket and Pfund series respectively. Line specrum becomes more complex for heavier atoms.

Bhor’S Model For Hydrogen Atom
Bhors model for hydrogen atom says that
1. the energy of an electron does not change with time.
The diagram shows the Lyman, Balmer and Paschen series of transitions for hydrogen atom.

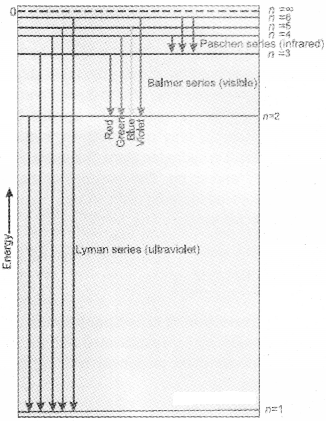
2. The frequency of radiation absorbed or emitted when transition occurs between two stationary states that differ in energy by ∆E, is given by :
\(v=\frac{\Delta E}{h}=\frac{E_{2}-E_{1}}{h}\)
E₁ and E₂ are the energies of the lower and higher allowed energy states respectively.
The angular momentum of an electron in a given stationary state can be expressed as in equation,

Bohr’s theory for hydrogen atom:
1. The stationary states for electron are numbered n = 1,2,3. These integral numbers are known as Principal quantum numbers.
2. The radii of the stationary states are expressed as:
r_n = n² a₀
where a₀ = 52.9 pm

3. The most important property associated with the electron, is the energy of its stationary state. It is
given by the expression, \(E_{n}=-R_{H}\left(\frac{1}{n^{2}}\right)\)
where R_H is called Rydberg constant and its value is 2.18 × 10^-18 J. The energy of the lowest state, also called as the ground state, is
E₁ = -2.18 × 10^-18 \(\left(\frac{1}{1^{2}}\right)\) = -2.18 × 10^-18 J. The energy of the stationary state for n = ∝, will be :
E₂ = -2.18 × 10^-18 J\(\left(\frac{1}{2^{2}}\right)\) = -0.545 × 10^-18 J.

When the electron is free from the influence of nucleus(n = ∞), the energy is taken as zero. When the electron is attracted by the nucleus and is present in orbit n, the energy is emitted and its energy is lowered. That is the reason for the presence of negative sign and depicts its stability relative to the reference state of zero energy and n = ∞

4. Bohr’s theory can also be applied to the ions containing only one electron, similar to that present in hydrogen atom. For example, He⁺ Li²⁺, Be³⁺ and so on. The energies of the stationary states associated with these hydrogen-like species are given by the expression,

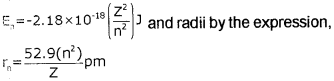
Explanation of Line Spectrum of Hydrogen
The frequency (v) associated with the absorption and emission of the photon can be evaluated by using equation,

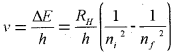
Limitations of Bohr’s Model
Bohr’s model was too simple to account for the following points:
1. It fails to account for the finer details (doublet, that is two closely spaced lines) of the hydrogen atom spectrum. This model is also unable to explain the spectrum of atoms other than hydrogen Further, Bohr’s theory was also unable to explain the splitting of spectral lines in the presence of magnetic field (Zeeman effect) or an electric field (Stark effect).
2. It could not explain the ability of atoms to form molecules by chemical bonds.

Towards Quantum Mechanical Model Of The Atom
Two important developments which contributed significantly in the formulation of a more suitable and general model for atoms were:

1. Dual behaviour of matter
2. Heisenberg uncertainty principle

Dual Behaviour of Matter
The French physicist, de Broglie proposed that matter, like radiation, should also exhibit dual behaviour i. e., both particle and wavelike properties. This means that just as the photon, electrons should. also have momentum as well as wavelength. de Broglie, from this analogy, gave the following relation between wavelength (λ) and momentum (p) of a material particle.
\(\lambda=\frac{h}{m v}=\frac{h}{p}\)

Heisenberg’s Uncertainty Principle
Werner Heisenberg a German physicist in 1927, stated uncertainty principle which is the consequence of dual behaviour of matter and radiation. It states that it is impossible to determine simultaneously, the exact position and exact momentum (or velocity) of an electron. Mathematically, it can be given as in equation,

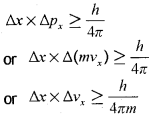
∆x is the uncertainty in position and ∆p_x (or ∆v_x) is the uncertainty in momentum (or velocity) of the particle. If the position of the electron is known with high degree of accuracy (∆x is small), then the velocity of the electron will be uncertain ∆v_x is large]. On the other hand, if the velocity of the electron is known precisely ( ∆v_x is small), then the position of the electron will be uncertain (∆x will be large). Thus, if we carry out some physical measurements on the electron’s position or velocity, the outcome will always depict a fuzzy or blur picture.

Significance of Uncertainty Principle
Heisenberg Uncertainty Principle rules out existence of definite paths or trajectories of electrons and other similar particles. The trajectory of an object is determined by its location and velocity at various moments. If we know where a body is at a particular instant and if we also know its velocity and the forces acting on it at that instant, we can tell where the body would be sometime later. We, therefore, conclude that the position of an object and its velocity fix its trajectory. The effect of Heisenberg Uncertainty Principle is significant only for motion of microscopic objects and is negligible for that of macroscopic objects.

Reasons for the Failure of the Bohr Model
In Bohr model, an electron is regarded as a charged particle moving in well defined circular orbits about the nucleus. The wave character of the electron is not considered in Bohr model. Further, an orbit is a clearly defined path and this path can completely be defined only if both the position and the velocity of the electron are known exactly at the same time. This is not possible according to the Heisenberg uncertainty principle. Bohr.model of the hydrogen atom, therefore, not only ignores dual behaviour of matter but also contradicts Heisenberg uncertainty principle. There was no point in extending Bohr model to other atoms. In fact, an insight into the structure of the atom was needed which could account for wave-particle duality of matter and be consistent with Heisenberg uncertainty principle. This came with the advent of quantum mechanics.

Quantum Mechanical Model Of Atom
Quantum mechanics is a theoretical science that deals with the study of motions of microscopic objects such as electrons.

In quantum mechanical model of atom, the behaviour of an electron in an atom is described by an equation known as Schrodinger wave equation. Fora system, such as an atom or molecule whose energy does not change with time, the Schrodinger equation written as Hψ = Eψ where H is a mathematical operator, called Hamiltonian operator, E is the total energy and ψ is the amplitude of the electron wave called wave function.

Hydrogen Atom And The Schrodinger Equation
The wave function ψ as such has no physical significance. It only represents the amplitude of the electron wave. However ψ² may be considered as the probability density of the electron cloud. Thus, by determining ψ² at different distances from the nucleus, it is possible to trace out or identify a region of space around the nucleus where there is high probability of locating an electron with a specific energy.

According to the uncertainty principle, it is not possible to determine simultaneously the position and momentum of an electron in an atom precisely. So Bohr’s concept of well defined orbits for electron in an atom cannot hold good. Thus, in quantum mechanical mode, we speak of probability of finding an electron with a particular energy around the nucleus. There are certain regions around the nucleus where probability of finding the electron is high. Such regions are called orbitals. Thus an orbital may be defined as the region in space around the nucleus where there is maximum probability of finding an electron having a specific energy.

Orbitals and Quantum Numbers
Orbitals in an atom can be distinguished by their size, shape and orientation. An orbital of smaller size means there is more chance of finding the electron near the nucleus. Similarly, shape and orientation mean that there is more probability of finding the electron along certain directions than along others. Atomic orbitals are precisely distinguished by what are known as quantum numbers. Each orbital is designated by three quantum numbers labelled as n, l and m_l

The principal quantum number n’ is a positive integer with value of n= 1, 2, 3 ……………

The principal quantum number determines the size and to large extent the energy of the orbital.

The principal quantum number also identifies the shell. With the increase in the value of ‘n’, the number of allowed orbital increases and are given by ‘n²’ Ait the orbitals of a given value of ‘n’ constitute a single shell of atom and are represented by the following letters
n= 1 2 3 4 ………………
Shell = K LM N ………………

Size of an orbital increases with increase of principal quantum number ‘n’. Since energy of the orbital will increase with increase of n.

Azimuthal quantum number, ‘F is also known as orbital angular momentum or subsidiary quantum number. It defines the three-dimensional shape of the orbital. For a given value of n, l can have n values ranging from 0 to (n – 1), that is, for a given value of n, the possible value of l are: l = 0, 1, 2, ……….. (n – 1)

Each shell consists of one or more subshells or sub-levels. The number of subshells in a principal shell is equal to the value of n. For example h the first shell (n = 1), there is only one sub-shell which corresponds to l = 0. There are two sub-shells (l= 0, 1) in the second shell (n = 2), three l= 0, 1, 2) and so on. Each sub-shell is assigned an azimuths! quantum number (l). Sub-shells corresponding to different values of l are represented by the following symbols.
l : 0 1 2 3 4 5 …………….
Notation for sub-shell : s p d f g h …………….

Magnetic orbital quantum number. ‘m_l’ gives information about the spatial orientation of the or bital with respect to standard set of co-ordinate axis. For any sub-shell (defined by T value) 21+ 1 values of m,are possible and these values are given by:
m, = -l, -(l-1), (l-2)… 0, 1… (l-2), (l-1), l Thus for l = 0, the only permitted value of m,= 0, [2(0) + 1 = 1, one s orbital].

Electron spin ‘s’:
George Uhlenbeck and Samuel Goudsmit proposed the presence of the fourth quantum number known as the electron spin quantum number (m_s). Spin angular momentum of the electron — a vector quantity, can have two orientations relative to the chosen axis. These two orientations are distinguished by the spin quantum numbers ms which can take the values of +½ or -½. These are called the two spin states of the electron and are. normally represented by two arrows, ↑ (spin up) and ↓ (spin down). Two electrons that have different m_s values (one +½ and the other -½) are said to have opposite spins. An orbital cannot hold more than two electrons and these two electrons should have opposite spins.

Shapes of Atomic Orbitals
The orbital wave function or V for an electron in an atom has no physical meaning. It is simply a mathematical function of the coordinates of the electron.

According to the German physicist, Max Bom, the square of the wave function (i.e., ψ²) at a point gives the probability density of the electron at that point.

For 1 s orbital the probability density is maximum at the nucleus and it decreases sharply as we move away from it. The region where this probability I density function reduces to zero is called nodal surfaces or simply nodes. In general, it has been found that ns-orbital has (n – 1) nodes, that is, number of nodes increases with increase of principal quantum number n.

These probability density variation can be visualised . in terms of charge cloud diagrams.

Boundary surface diagrams of constant probability density for different orbitals give a fairly good representation of the shapes of the orbitals. In this representation, a boundary surface or contour surface is drawn in space for an orbital on which the value of probability density |ψ|² is constant. Boundary ‘ surface diagram for a s orbital is actually a sphere centred on the nucleus. In two dimensions, this sphere looks like a circle. It encloses a region in which probability of finding the electron is about 90%. The s-orbitals are spherically symmetric, that is, the probability of finding the electron at a given distance is equal in all directions.

unlike s-orbitals, the boundary surface diagrams of p orbitals are not spherical. Instead, each p orbital consists of two sections called lobes that are on either side of the plane that passes through the nucleus. The probability density function is zero on the plane where the two lobes touch each other. The size, shape and energy of the three orbitals are identical. They differ, however, in the way the lobes are oriented. Since the lobes may be considered to lie along the x, y or z-axis, they are given the designations 2p_x, 2p_y, and 2p_z. It should be understood, however, that there is no simple relation between the values of m, (-1, 0 and+1) and the x, y and z directions. For our purpose, it is sufficient to remember that, because there are three possible values of m, there are, therefore, three p orbitals whose axes are mutually perpendicular. Like s orbitals, p orbitals increase in size and energy with increase in the principal quantum number

The number of nodes are given by (n -2), that is number of radial node is 1 for 3p orbital, two for 4p orbital and so on.

For l = 2, the orbital is known as d-orbital and the minimum value of principal quantum number (n) has to be 3 as the value of l cannot be greater than n-1. There are five m; values (-2, -1, 0, +1 and +2) for l = 2 and thus there are five d orbitals. The five d-orbitals are designated as d_xy, d_yz, d_xz, d_x²-y² and d_z². The shapes of the first fourd-orbitals are similar to each other, whereas that of the fifth one, d_z², is different from others, but all five 3d orbitals are equivalent in energy. The d orbitals for which n is greater than 3 (4d, 5d…) also have shapes similar to 3d orbital, but differ in energy and size.

Besides the radial nodes (i.e., probability density function is zero), the probability density functions for the np and nd orbitals are zero at the plane (s), passing through the nucleus (origin). For example, in case of p_z orbital, xy-plane is a nodal plane, in case of d_xy orbital, there are two nodal planes passing through the origin and bisecting the xy plane containing z-axis. These are called angular nodes and number of angular nodes are given by T, i.e., one angular node for p orbitals, two angular nodes for cf orbitals and so on. The total number of nodes are given by (n-1), i.e., sum of I angular nodes and (n-l-1) radial nodes.

Energies Of Orbitals
The order of energy of orbitals in single electron sys-tem are given below:
1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f The orbitals having same energy are called degenerate.

Filling Of Orbitals In Atom
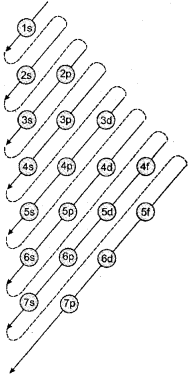
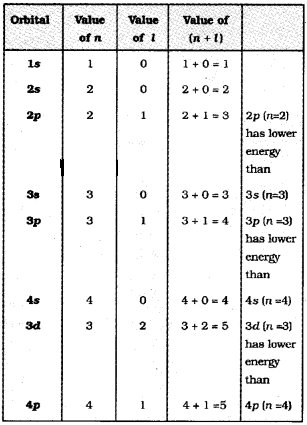
Aufbau principle: According to this principle in the ground state of an atom, an electron will occupy the orbital of lowest energy and orbitals are occupied by electrons in the order of increasing energy.

Pauli’s exclusion principle: Pauli’s exclusion principle states that ‘no two electrons in an atom can have the same values for all the four quantum numbers’

Since the electrons in an orbital must have the same n, I and m quantum numbers, if follows that an orbital can contain a maximum of two electrons provided their spin quantum numbers are different. This is an important consequence of Pauli’s exclusion principle which says that an orbital can have maximum two electrons and these must have opposite spins.

Hund’s rule of maximum multiplicity :
This rule states that electron pairing in orbitals of same energy will not take place until each available orbital of a given subshell is singly occupied (with parallel spin).
The rule can be illustrated by taking the example of carbon atom. The atomic number of carbon is 6 and its electronic configuration is 1s²2s²2p². The two electrons of the 2p subshell can be distributed in the following three ways.

According to Hund’s rule, the configuration in which the two unpaired electron occupying 2px, and 2py orbitals with parallel spin is the correct configuration of carbon.

Exceptional configurations of chromium and copper
The electronic configuration of Cr (atomic number 24) is expected to be [Ar] 4s² 3d⁴, but the actual configuration is [Ar] 4s¹ 3d⁵. Similarly, the actual configuration of Cu (At. No. 29) is [Ar] 4s¹ 3d¹⁰ instead of the expected configuration [Ar] 4s² 3d⁹.

This is because of the fact that exactly half filled or completely filled orbitals (i.e., d⁵, d¹⁰, f⁷, f¹⁴) have lower energy and hence have extra stability.

Plus One Chemistry Notes