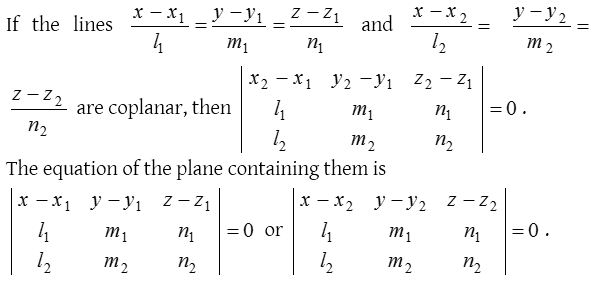What is a Plane in 3D?

What is a Plane in 3D?

https://www.youtube.com/watch?v=3dNL_aOVuQ4

Definition of plane and its equations

If point P(x, y, z) moves according to certain rule, then it may lie in a 3-D region on a surface or on a line or it may simply be a point. Whatever we get, as the region of P after applying the rule, is called locus of P. Let us discuss about the plane or curved surface. If Q be any other point on it’s locus and all points of the straight line PQ lie on it, it is a plane. In other words if the straight line PQ, however small and in whatever direction it may be, lies completely on the locus, it is a plane, otherwise any curved surface.

1. General equation of plane: Every equation of first degree of the form Ax + By + Cz + D = 0 represents the equation of a plane. The coefficients of x, y and z i.e., A, B, C are the direction ratios of the normal to the plane.
2. Equation of co-ordinate planes: XOY-plane : z = 0, YOZ -plane : x = 0, ZOX-plane : y = 0.
3. Equation of plane in various forms:
   1. Intercept form: If the plane cuts the intercepts of length a, b, c on co-ordinate axes, then its equation is
      .
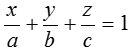   2. Normal form: Normal form of the equation of plane is , where l, m, n are the d.c.’s of the normal to the plane and p is the length of perpendicular from the origin.
4. Equation of plane in particular cases:
   Equation of plane through the origin is given by Ax + By + Cz = 0.
   i.e, if D = 0, then the plane passes through the origin.
5. Equation of plane parallel to co-ordinate planes or perpendicular to co-ordinate axes:
   1. Equation of plane parallel to YOZ-plane (or perpendicular to x-axis) and at a distance ‘a’ from it is x = a.
   2. Equation of plane parallel to ZOX-plane (or perpendicular to y-axis) and at a distance ‘b’ from it is y = b.
   3. Equation of plane parallel to XOY-plane (or perpendicular to z-axis) and at a distance ‘c’ from it is z = c.
6. Equation of plane perpendicular to co-ordinate planes or parallel to co-ordinate axes:
   1. Equation of plane perpendicular to YOZ-plane or parallel to x-axis is By + Cz + D = 0.
   2. Equation of plane perpendicular to ZOX-plane or parallel to y-axis is Ax + Cz + D = 0.
   3. Equation of plane perpendicular to XOY-plane or parallel to z-axis is Ax + By + D = 0.
7. Equation of plane parallel to a given plane:
   Plane parallel to a given plane ax + by + cz + d = 0 is ax + by + cz + d’ = 0, i.e. only constant term is changed.
8. Equation of plane passing through the intersection of two planes:
   Equation of plane through the intersection of two planes P = a₁x + b₁y + c₁z + d₁ = 0 and Q = a₂x + b₂y + c₂z + d₂ = 0 is P + λQ = 0, where λ is the parameter.

Equation of plane passing through the given point

1. Equation of plane passing through a given point:
   Equation of plane passing through the point (x₁, y₁, z₁) is A(x – x₁) + B(y – y₁) + C(z – z₁) = 0, where A, B and C are d.r.’s of normal to the plane.
2. Equation of plane through three points:
   The equation of plane passing through three non-collinear points (x₁, y₁, z₁), (x₂, y₂, z₂) and (x₃, y₃, z₃) is
   

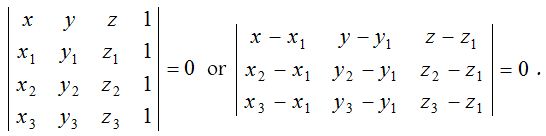
Foot of perpendicular from a point A(α, β, γ) to a given plane ax + by + cz + d = 0.

If AP be the perpendicular from A to the given plane, then it is parallel to the normal, so that its equation is

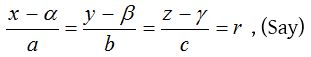
Any point P on it is (ar + α, br + β, cr + γ). It lies on the given plane and we find the value of r and hence the point P.

1. Perpendicular distance:
   The length of the perpendicular from the point P(x₁, y₁, z₁) to the plane ax + by + cz + d = 0 is
   
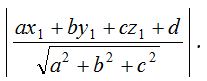
   Distance between two parallel planes Ax + By + Cz + D₁ = 0 and Ax + By + Cz + D₂ = 0 is
   
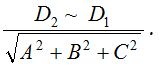
2. Position of two points w.r.t. a plane:
   Two points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) lie on the same or opposite sides of a plane ax + by + cz + d = 0 according to a₁x + b₁y + c₁z + d and a₂x + b₂y + c₂z + d are of same or opposite signs. The plane divides the line joining the points P and Q externally or internally according to P and Q are lying on same or opposite sides of the plane.

Angle between two planes

Angle between the planes is defined as angle between normals to the planes drawn from any point. Angle between the planes a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0 is

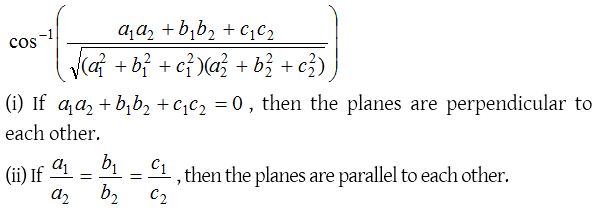
Equation of planes bisecting angle between two given planes

Equations of planes bisecting angles between the planes a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0 are

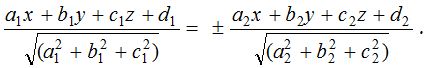
(i) If angle between bisector plane and one of the plane is less than 45o, then it is acute angle bisector, otherwise it is obtuse angle bisector.
(ii) If a₁a₂ + b₁b₂ + c₁c₂ is negative, then origin lies in the acute angle between the given planes provided d₁ and d₂ are of same sign and if a₁a₂ + b₁b₂ + c₁c₂ is positive, then origin lies in the obtuse angle between the given planes.

Image of a point in a plane

Let P and Q be two points and let π be a plane such that
(i) Line PQ is perpendicular to the plane π, and
(ii) Mid-point of PQ lies on the plane π.
Then either of the point is the image of the other in the plane π.
To find the image of a point in a given plane, we proceed as follows
(i) Write the equations of the line passing through P and normal to the given plane as

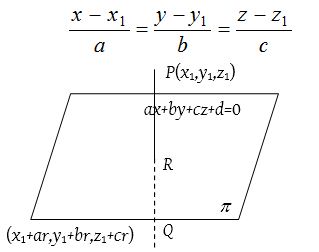
(ii) Write the co-ordinates of image Q as (x₁ + ar, y₁ + br, x₁ +cr).
(iii) Find the co-ordinates of the mid-point R of PQ.
(iv) Obtain the value of r by putting the co-ordinates of R in the equation of the plane.
(v) Put the value of r in the co-ordinates of Q.

Coplanar lines

Lines are said to be coplanar if they lie in the same plane or a plane can be made to pass through them.
Condition for the lines to be coplanar: