Perpendiculars from a Point On the Line and from a Point Off the Line
Perpendicular – lines (or segments) which meet to form right angles.
Perpendicular from a point ON a line
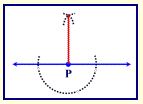
Given: Point P is on a given line
Task: Construct a line through P perpendicular to the given line.
Directions:
- Place your compass point on P and sweep an arc of any size that crosses the line twice (below the line). You will be creating (at least) a semicircle. (Actually, you may draw this arc above OR below the line.)
- STRETCH THE COMPASS LARGER!!
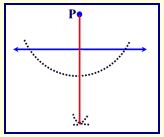
- Place the compass point where the arc crossed the line on one side and make a small arc below the line. (The small arc could be above the line if you prefer.)
- Without changing the span on the compass, place the compass point where the arc crossed the line on the OTHER side and make another arc. Your two small arcs should be crossing.
- With your straightedge, connect the intersection of the two small arcs to point P.
This new line is perpendicular to the given line.
Explanation of construction: Remember the construction for bisect an angle? In this construction, you have bisected the straight angle P. Since a straight angle contains 180 degrees, you have just created two angles of 90 degrees each. Since two right angles have been formed, a perpendicular exists.
Perpendicular from a point Off a line
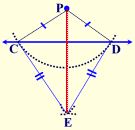
Given: Point P is off a given line
Task: Construct a line through P perpendicular to the given line.
Directions:
- Place your compass point on P and sweep an arc of any size that crosses the line twice.
- Place the compass point where the arc crossed the line on one side and make an arc ON THE OPPOSITE SIDE OF THE LINE.
- Without changing the span on the compass, place the compass point where the arc crossed the line on the OTHER side and make another arc. Your two new arcs should be crossing on the opposite side of the line.
- With your straightedge, connect the intersection of the two new arcs to point P.
This new line is perpendicular to the given line.
Explanation of construction: To understand the explanation, some additional labeling will be needed. Label the point where the arc crosses the line as points C and D. Label the intersection of the new arcs on the opposite side as point E. Draw segments \(\overline { PC }\), \(\overline { PD }\), \(\overline { CE }\) and \(\overline { DE }\). By the construction, PC = PD and EC = ED. Now, remember a locus theorem: The locus of points equidistant from two points (C and D), is the perpendicular bisector of the line segment determined by the two points. Hence, \(\overline { PE }\) is the perpendicular bisector of \(\overline { CD }\).
