What is a Permutation? Can Permutations have Repetition?
Definition of permutation:
The ways of arranging or selecting a smaller or an equal number of persons or objects at a time from a given group of persons or objects with due regard being paid to the order of arrangement or selection are called the (different) permutations.
For example : Three different things a, b and c are given, then different arrangements which can be made by taking two things from three given things are ab, ac, bc, ba, ca, cb.
Therefore the number of permutations will be 6.
The notation for a permutation: nPr
n is the total number of objects
r is the number of objects chosen (want)
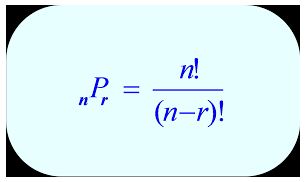
(1) The Factorial: Factorial notation: Let n be a positive integer. Then, the continued product of first n natural numbers is called factorial n, to be denoted by n !.
Also, we define 0 ! = 1.
when n is negative or a fraction, n ! is not defined.
Thus, n ! = n (n – 1) (n – 2) ……3.2.1.
(2) Exponent of Prime p in n !: Let p be a prime number and n be a positive integer. Then the last integer amongst 1, 2, 3, …….(n – 1), n which is divisible by p is , where denotes the greatest integer less than or equal to .
Can Permutations have Repetition?
Number of permutations without repetition
(1) Arranging n objects, taken r at a time equivalent to filling r places from n things.
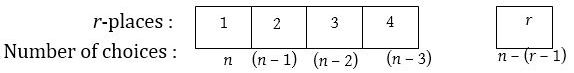
The number of ways of arranging = The number of ways of filling r places.
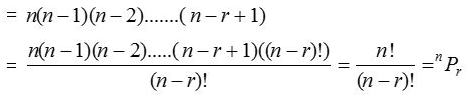
(2) The number of arrangements of n different objects taken all at a time = nPn = n!
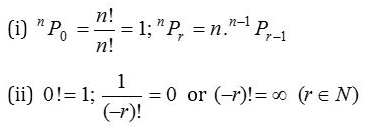
Number of permutations with repetition
(1) The number of permutations (arrangements) of n different objects, taken r at a time, when each object may occur once, twice, thrice,……..upto r times in any arrangement = The number of ways of filling r places where each place can be filled by any one of n objects.

The number of permutations = The number of ways of filling r places = (n)r.
(2) The number of arrangements that can be formed using n objects out of which p are identical (and of one kind) q are identical (and of another kind), r are identical (and of another kind) and the rest are distinct is .
Conditional permutations
- Number of permutations of n dissimilar things taken r at a time when p particular things always occur = n−pCr−p r!.
- Number of permutations of n dissimilar things taken r at a time when p particular things never occur = n−pCr r!.
- The total number of permutations of n different things taken not more than r at a time, when each thing may be repeated any number of times, is .
- Number of permutations of n different things, taken all at a time, when m specified things always come together is m! × (n – m + 1)!.
- Number of permutations of n different things, taken all at a time, when m specified things never come together is n! – m! × (n – m + 1)!.
- Let there be n objects, of which m objects are alike of one kind, and the remaining (n – m) objects are alike of another kind. Then, the total number of mutually distinguishable permutations that can be formed from these objects is
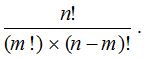
The above theorem can be extended further i.e., if there are n objects, of which p1 are alike of one kind; p2 are alike of another kind; p3 are alike of 3rd kind;……; pr are alike of rth kind such that p1 + p2 + …… + pr = n; then the number of permutations of these n objects is
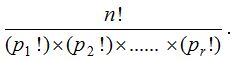
Circular permutations
In circular permutations, what really matters is the position of an object relative to the others.
Thus, in circular permutations, we fix the position of the one of the objects and then arrange the other objects in all possible ways.
There are two types of circular permutations :
(i) The circular permutations in which clockwise and the anticlockwise arrangements give rise to different permutations, e.g. Seating arrangements of persons round a table.
(ii) The circular permutations in which clockwise and the anticlockwise arrangements give rise to same permutations, e.g. arranging some beads to form a necklace.
Difference between clockwise and anti-clockwise arrangement :
If anti-clockwise and clockwise order of arrangement are not distinct e.g., arrangement of beads in a necklace, arrangement of flowers in garland etc. then the number of circular permutations of n distinct items is .
(i) Number of circular permutations of n different things, taken r at a time, when clockwise and anticlockwise orders are taken as different is .
(ii) Number of circular permutations of n different things, taken r at a time, when clockwise and anticlockwise orders are not different is .
Theorems on circular permutations
Theorem (i) : The number of circular permutations of n different objects is (n – 1)!.
Theorem (ii) : The number of ways in which n persons can be seated round a table is (n – 1)!.
Theorem (iii) : The number of ways in which n different beads can be arranged to form a necklace, is ½(n – 1)!.
Examples:

Permutations with Special Arrangements:
Example: Using the letters in the word ” square “, tell how many 6-letter arrangements, with no repetitions, are possible if the :
a) first letter is a vowel.
b) vowels and consonants alternate, beginning with a consonant.
Solution:
Part a: Hint: When working with “arrangements”, it is often helpful to put lines down to represent the locations of the items.
For this problem, six “locations” are needed for 6-letter arrangements.
_____ • _____ • _____ • _____ • _____ • _____
The first locations must be a vowel (u, a, e). There are three ways to fill the first location.
__3___ • _____ • _____ • _____ • _____ • _____
After the vowel has been placed in the first location, there are 5 letters left to be arranged in the remaining five spaces.
__3__ • __5__ • __4__ • __3__ • __2__ • __1__ or
3 · 5P5 = 3 · 120 = 360
Part b: Six locations are needed for the 6-letter arrangements.
_____ • _____ • _____ • _____ • _____ • _____
Beginning with a consonant, every other location must be filled with a consonant. (s, q, r )
__3__ • _____ • __2___ • _____ • ___1__ • _____
The remaining locations are filled with the remaining three vowels:
__3__ • __3___ • __2___ • __2___ • ___1__ •___1__ = 36.
