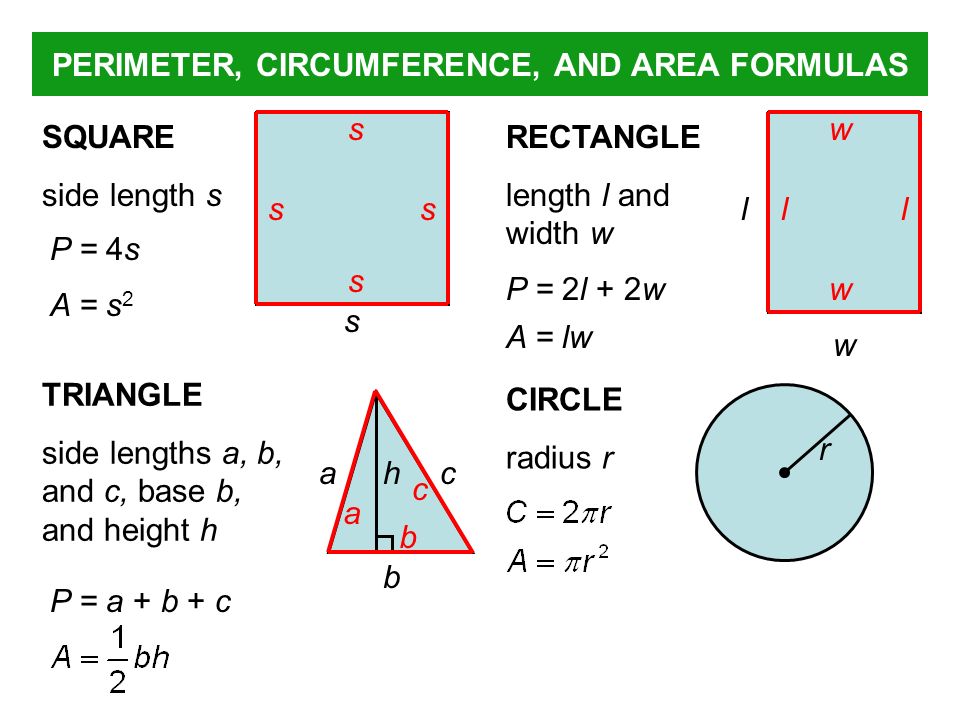
Perimeter and Circumference
Perimeter is the word used to describe the distance around the outside of a figure.
To find the perimeter, add together the lengths of all of the sides of the figure.
Refresh your polygon memories:
When working with perimeter, references may be made to the names of polygons. Listed at the left are some of the more common polygons whose names you should know.
Remember that “regular polygons” are polygons whose sides are all the same length and whose angles are all the same size. Not all polygons are “regular”.
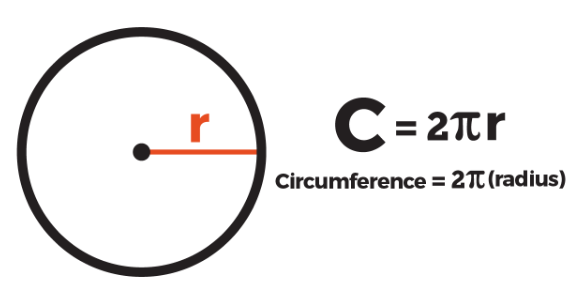
Circumference is the word used to describe the distance around the outside of a circle.
Like perimeter, the circumference is the distance round the outside of the figure. Unlike perimeter, in a circle there are no straight segments to measure, so a special formula is needed
Example 1: Ed and Carol are jogging around a circular track in the park. The diameter of the track is 0.8 miles. Find, to the nearest mile, the number of miles they jogged if they made two complete trips around the track.
Solution: C = πd
= (3.141592654)(0.8) = 2.513274123 miles (one trip)
2(2.513274123) = 5.026548246 = 5 miles
Example 2: For an art project at school, you need a piece of string long enough to wrap around the outer edge of this starfish. What is the shortest possible length for the string?
Solution:
Perimeter = 2 + 1.5 + 1 + 2 + 1.5 + 2 + 2 + 3 + 2.5 + 2
= 19.5 inches
