How do you Find Percentage Profit or Loss?
https://www.youtube.com/watch?v=vDAUwgyUpao
Profit and Loss
Cost Price:
The price that a person spends to purchase or manufacture some goods is called the cost price. In short, we write C.P. for cost price.
Selling Price:
The price at which a shopkeeper or a person sells his good is called the selling price. In short, we write S.P. for selling price.
| In case of profit | In case of Loss |
| Profit = S.P. – C.P. | Loss = C.P. – S.P. |
| S.P. = Profit + C.P. | C.P. = Loss + S.P. |
| C.P. = S.P. – Profit | S.P. = C.P. – Loss |
Profit and Loss Problems with Solutions
1. Find the profit or loss:
(i) C.P. = ₹ 176.50 ; S.P. = ₹ 215.80
(ii) C.P. = ₹ 499 ; S.P. = ₹ 357
(iii) C.P. = ₹ 44,450 ; S.P. = ₹ 38,578
Solution:
(i) Here S.P. > C.P., therefore
Profit = S.P. – C.P. = ₹ 215.80 – ₹ 176.50
= ₹ 39.30
(ii) Here S.P. < C.P., therefore
Loss = C.P. – S.P.
= ₹ 499 – ₹ 357 = ₹ 142
(iii) Here C.P. > S.P.
So, Loss = C.P. – S.P.
= ₹ 44,450 – ₹ 38,578
= ₹ 5,872
2. A trade purchased 10 quintals of wheat from a farmer for ₹ 8,750. He sold it at ₹ 11.50 per kg. Find the amount of profit/ loss of the trader.
Solution:
We know that 1 quintal = 100 kg
∴ 10 quantials = 10 × 100 kg = 1000 kg
So, the cost price of 1000 kg wheat = ₹ 8,750
Also the selling price of 1kg wheat = ₹ 11.50
Therefore, the S.P. of 1000 kg wheat
= 1000 × 11.50
= ₹ 11,500.00
Since S.P. > C.P.
So, the profit = S.P. – C.P.
= ₹ 11,500 – ₹ 8750
= ₹ 2750
Thus, the profit of the trader is ₹ 2750.
3. A shopkeeper earns a profit of ₹ 325.75 on each sewing machine. If the C.P. of a machine is ₹ 2018.50, what is the selling price ?
Solution:
Profit = ₹ 325.75, Cost Price = ₹ 2018.50
∴ S.P. = Profit + C.P.
= ₹ 325.75 + ₹ 2018.50
= ₹ 2344.25
4. A milkman buys 20 litres of milk from a dairy for ₹ 370. He sells it at the rate of ₹ 21.50 per litre. Find his profit or loss.
Solution:
C.P. of 20 litre milk = ₹ 370
S.P. of 1 litre milk = ₹ 21.50
Therefore, S.P. of 20 litres milk
= ₹ 21.50 × 20
= ₹ 430
Clearly, S.P. > C.P., so profit
= ₹ 430 – ₹ 370
= ₹ 60
5. A girl purchased 12 packet for ₹ 156. Each packet contains 10 pencils. She sold all the pencils at a price of ₹ 2 per pencil. Find the profit or loss.
Solution:
12 packets have 12 × 10 = 120 pencils.
C.P. for 120 pencils = ₹ 156
Selling price for 1 pencil = ₹ 2
Therefore, the S.P. of 120 pencil
= 120 × ₹ 2 = ₹ 240
Since S.P. > C.P., therefore, there will be the profit.
Profit = ₹ 240 – ₹ 156
= ₹ 84.
6. Bela purchased a second hand car for ₹ 89,000. She spent ₹ 21,000 on its repair and sold it to Aman for ₹ 1,10,000. Find her profit or loss in this transaction.
Solution:
The amount at which the Bela purchased the car = ₹ 89,000
The amount he spent on repair = ₹ 21000
Therefore, the cost price
= ₹ 89000 + ₹ 21,000
= ₹ 1,10,000
Note : Total C.P. = actual cost price + overheads.
Since S.P. = ₹ 1,10,000
⇒ S.P. = C.P.
Therefore Bela neither suffered loss nor gained any profit.
Profit or Loss Percent
In order to calculate profit or loss in percent, we use the following formulae :
1.
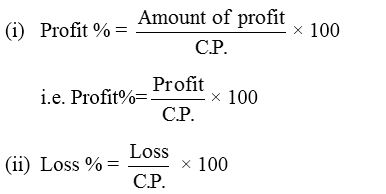
2. Profit or loss percent is always calculated on the C.P. Also we can find

Profit or Loss Percent Problems with Solutions
1. Find the profit or loss percent if:
(i) C.P. = ₹ 500; S.P. = ₹ 600
(ii) C.P. = ₹ 600; S.P. = ₹ 500
Solution:
(i) We have, C.P. = ₹ 500, S.P. = ₹ 600
Clearly S.P. > C.P.
Therefore profit = ₹ 600 – ₹ 500 = ₹ 100
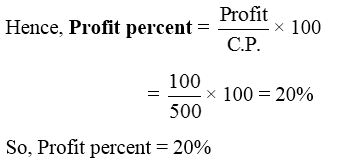
(ii) We have, C.P. = ₹ 600, S.P. = ₹ 500
Clearly C.P. > S.P.
Loss = C.P. – S.P. = ₹ 600 – ₹ 500 = ₹ 100
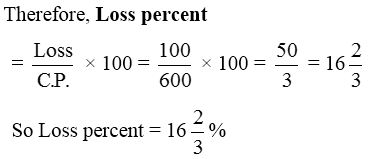
2. Karim bought 150 dozens of pencils at ₹ 20 a dozen. He sold them at ₹ 2.50 per pencil. Find the profit or loss percent.
Solution:
C.P. of one dozen of pencils = ₹ 20
C.P. of 150 dozens of pencils = ₹ 20 × 150 = ₹ 3000
Now, S.P. of 1 pencil = ₹ 2.50
S.P. of 1 dozen (i.e. 12) pencils = ₹ 2.50 × 12 = ₹ 30
Therefore, S.P. of 150 dozen pencils = 150 × 30 = ₹ 4500
Profit = S.P. – C.P. = ₹ (4500 – 3000) = ₹ 1500
3. Neelu bought 2400 bananas at ₹ 15 a dozen. She sold 1350 of them at ₹ 4 for 2 and remaining at ₹ 8 for 5. Find her gain or loss percent.
Solution:
C.P. of 12 bananas = ₹ 15
C.P. of 1 banana = \(\frac { 15 }{ 12 }\)
C.P. of 2400 bananas = \(\frac { 15 }{ 12 }\) × 2400 = ₹ 3000
S.P. of 2 bananas = ₹ 4
S.P. of 1 banana = \(\frac { 4 }{ 2 }\)
S.P. of 1350 bananas = \(\frac { 4 }{ 2 }\) × 1350 = ₹ 2700
Remaining bananas = 2400 – 1350 = 1050
S.P. of 5 remaining bananas = ₹ 8
S.P. of 1 remaining bananas = \(\frac { 8 }{ 5 }\)
S.P. of 1050 remaining bananas = \(\frac { 8 }{ 5 }\) × 1050 = ₹ 1,680
Total S.P. = ₹ 2700 + ₹ 1680 = ₹ 4380
Gain = ₹ (4380 – 3000) = ₹ 1380
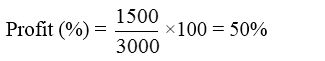
4. A book wholesaler sold 300 copies of a book at a profit of 15%. If C.P. of a book is ₹ 48, find the selling price of the books.
Solution:
C.P. of 1 copy of the book = ₹ 48
C.P. of 300 copies of the book = 300 × 48 = ₹ 14400
Profit (%) = 15%, Profit = \(\frac { 15 }{ 100 }\) × 14400 = ₹ 2160
Therefore, S.P. of books = 14400 + 2160 = ₹ 16560
5. A horse bought for ₹ 8000 was sold at a loss of 6%. At what price was the horse sold ?
Solution:
C.P. = 8000, Loss (%) = 6%
Loss = \(\frac { 6 }{ 100 }\) ×8000 = ₹ 480
Therefore, S.P. = C.P. – Loss
= 8000 – 480 = ₹ 7520
6. An old bike bought for ₹ 2000 is sold for ₹ 2200. Find the profit and the profit % (or Gain%).
Solution:
C.P. of the old bike = ₹ 2000
S.P. of the old bike = ₹ 2200
Clearly, S.P. > C.P.
So, Profit = S.P. – C.P. = 2200 – 2000 = ₹ 200
Therefore, gain %