What are Parallel lines and Transversals?
Parallel lines:
Two lines l and m are said to be parallel if
(i) they lie in the same plane
(ii) they do not intersect when produced indefinitely in either direction and we write l || m (which is read as ‘l is parallel to m‘)
l || m also implies that m || l.
 The distance between two parallel lines is same everywhere or if the perpendicular distances between two lines are equal, lines are parallel, other wise not.
The distance between two parallel lines is same everywhere or if the perpendicular distances between two lines are equal, lines are parallel, other wise not.
For example, the distance between two Railway lines.

Transversal line:
A line which intersect two or more given lines at distinct points, is called a transversal of the given lines.
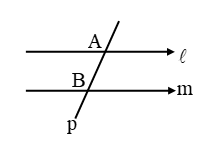 Here l || m and p is transversal line.
Here l || m and p is transversal line.
Part of transversal which is between the two lines is called intercept (AB).
Angles formed when a transversal cuts two lines:
Let two lines p and q be cut by a transversal t, then the following angles are formed.
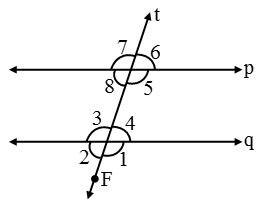
Exterior Angles
Angles which do not contain the segment of the transversal between the two lines are called exterior angles.
Interior Angles
The angles whose arms include the line segment of the transversal between the two lines are called interior angles.
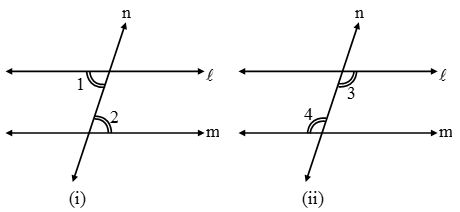
Corresponding Angles
Observe the angles marked in each of the figure.
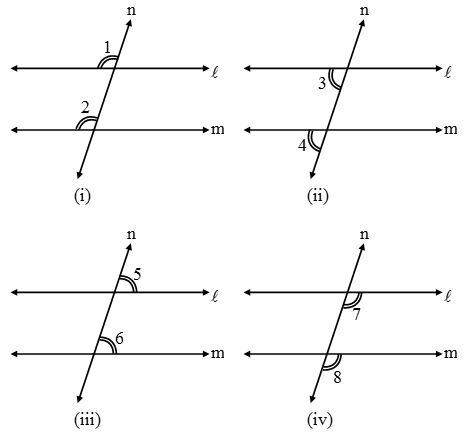 The angles which
The angles which
(i) have different vertices
(ii) lie on the same side of the transversal and
(iii) are in corresponding positions (above or below, left or right) relative to the two lines are called corresponding angles.
In other words, two angles on the same side of the transversal either above or below the two given lines are called corresponding angles.
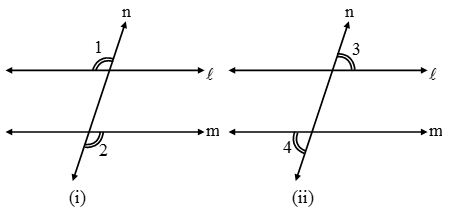
Alternate Interior Angles
 Alternate interior angles:
Alternate interior angles:
(i) have different vertices,
(ii) lie on opposite side of the transversal, and
(iii) lie between the two lines.
In other words, A pair of angles in which one arm of each of the angle lies on opposite side of the transversal and other arm of the angle is the segment of the transversal, made by the two line is called a pair of alternate interior angles.
Alternate Exterior Angles
 A pair of angles in which one arm of both the angles is on opposite side of the transversal and whose other arms do not include the segment of the transversal, made by the two lines, and are directed in opposite sides of segment of the transversal is called a pair of alternate exterior angles.
A pair of angles in which one arm of both the angles is on opposite side of the transversal and whose other arms do not include the segment of the transversal, made by the two lines, and are directed in opposite sides of segment of the transversal is called a pair of alternate exterior angles.
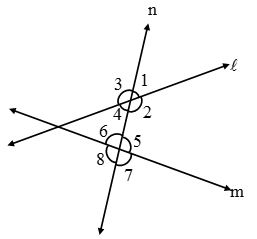
| S. No. | Name of angles | Angles |
| (i) | Interior angles | ∠2, ∠4, ∠5 and ∠6 |
| (ii) | Exterior angles | ∠1, ∠3, ∠7 and ∠8 |
| (iii) | Pairs of corresponding angles | ∠1 & ∠5, ∠2 & ∠7, ∠3 & ∠6, ∠4 & ∠8 |
| (iv) | Pairs of alternate interior angles | ∠4 & ∠5 and ∠2 & ∠6 |
| (v) | Pairs of alternate exterior angles | ∠3 & ∠7 and ∠1 & ∠8 |
| (vi) | Pairs of interior angles on the same side of the transversal | ∠4 & ∠6 and ∠2 & ∠5 |
| (vii) | Pairs of exterior angles on the same side of the transversal | ∠3 & ∠8 and ∠1 & ∠7 |
Note:
- If two or more parallel lines are cut by a transversal, then each pair of the corresponding angles have equal measure.
- If two parallel lines are cut by a transversal, the pair of alternate (interior as well as exterior) angles are equal.
- If two parallel lines are cut by a transversal, then each pair of interior angles as well as exterior angles on the same side of the transversal are supplementary.
* Part of transversal which is between the two lines is called intercept (AB).
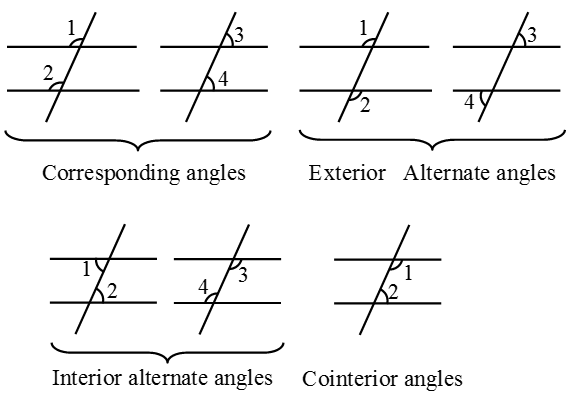
- Two angles on the same side of a transversal are known as the corresponding angles if both lie either above the two lines or below the two lines.
- The pairs of interior angles on the same side of the transversal are called pairs of consecutive interior angles.
- If a transversal intersect two parallel lines, then each pair of corresponding angles are equal.
- If a transversal intersects two parallel lines, then each pair of alternate interior angles are equal .
- If a transversal intersects two lines in such a way that a pair of alternate interior angles are equal, then the two lines are parallel.
- If a transversal intersects two parallel lines, then each pair of consecutive interior angles are supplementary.
- If a transversal intersects two lines in such a way that a pair of consecutive interior angles are supplementary, then the two lines are parallel.
- If two parallel lines are intersected by a transversal, the bisectors of any pair of alternate interior angles are parallel.
- If two parallel lines are intersected by a transversal, then bisectors of any two corresponding angles are parallel.
- If the bisectors of a pair of corresponding angles formed by a transversal with two given lines are parallel, prove that the given lines are parallel.
- If a line is perpendicular to one of two given parallel lines, then it is also perpendicular to the other line.
- If a side of a triangle is produced, the exterior angle so formed is equal to the sum of two interior opposite angles.
- If all sides of a polygon are equal it is called a regular polygon.
- Sum of all the interior angles of a polygon of n-sides = (n – 2) × 180º (n ≥ 3)
- Each interior angle of a regular polygon of n-sides
\(=\frac{(n-2)\times 180{}^\text{o}}{n} \) - Sum of all the exterior angles formed by producing the sides of polygon = 360º.
- No. of sides of polygon
\(=\frac{\text{360 }\!\!{}^\text{o}\!\!\text{ }}{\text{180 }\!\!{}^\text{o}\!\!\text{ -}\,\,\text{each}\,\,\text{interior}\,\,\text{angle}} \)
Parallel lines and Transversals Problems With Solutions
Example 1: In figure m || n and ∠1 = 65º. Find ∠5 and∠8.
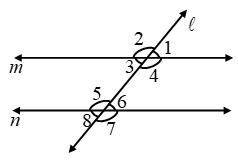
Solution: We have,
∠1 = ∠3 [Vertically opposite angles]
and, ∠3 = ∠8 [Corresponding angles]
∴ ∠1 = ∠8
⇒ ∠8 = 65º [∵ ∠1 = 65º (Given)]
Now, ∠5 + ∠8 = 180º
⇒ ∠5 + 65º = 180º
⇒ ∠5 = 180º – 65º = 115º
Thus, ∠5 = 115º and ∠8 = 65º.
Example 2: In figure m || n and angles 1 and 2 are in the raito 3 : 2. Determine all the angles from 1 to 8.
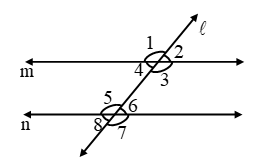
Solution: It is given that ∠1 : ∠2 = 3 : 2. So, let
∠1 = 3xº and ∠2 = 2xº
But ∠1 and ∠2 form a linear pair.
∴ ∠1 + ∠2 = 180º
⇒ 3xº + 2xº = 180º ⇒5xº = 180º
⇒ x = = 36º
∴ ∠1 = 3xº = (3 × 36)º = 108º
and, ∠2 = 2xº = (2 × 36)º = 72º
Now, ∠1 = ∠4 and ∠2 = ∠3
[ Vertically opposite angles]
∴ ∠4 = 72º and ∠3 = 108º
Now, ∠6 = ∠2º and ∠3 = ∠7
[Corresponding angles]
⇒ ∠6 = 72º and ∠7 = 108º [∵ ∠2 = 72º]
Again, ∠5 = ∠7 and ∠8 = ∠6
∴∠5 = 108º and ∠8 = 72º
Hence, ∠1 = 108º, ∠2 = 72º, ∠3 = 108º,
∠4 = 72º, ∠5 = 108º ∠6 = 72º, ∠7 = 108º
and ∠8 = 72º.
Example 3: In figure AB || DC and AD || BC. Prove that ∠DAB = ∠DCB.
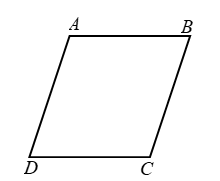
Solution: Since AD || BC and AB is a transversal intersecting them at A and B respectively. Therefore
∠DAB + ∠ABC = 180º
[Consecutive interior angles] …(i)
Again, AB || CD and BC is a transversal interacting them at B and C respectively. Therefore,
∠ABC + ∠DCB = 180º
[Consecutive interior angles] ….(ii)
From (i) and (ii), we get
∠DAB + ∠ABC = ∠ABC + ∠DCB
⇒ ∠DA B = ∠DCB
Example 4: In figure AB || CD. Determine ∠a
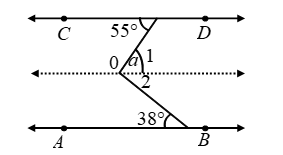
Solution: Through O draw a line l parallel to both AB and CD.
Clearly, ∠a = ∠1 + ∠2 ….(ii)
Now, ∠1 = 55º [Alternate ∠s]
and ∠2 = 38º [Alternate ∠s]
∴ ∠a = 55º + 38º [Using (i)]
⇒ ∠a = 93º.
Thus, ∠a = 93º
Example 5: In figure AB || CD. Determine X.
Solution: Through O, draw a line l parallel to both AB and CD. Then,
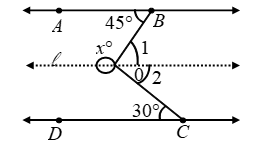
∠1 = 45º [Alternate ∠s]
and ∠2 = 30º [Alternate ∠s]
∴ ∠BOC = ∠1 + ∠2 = 45º + 30º = 75º
So, x = 360 – ∠BOC = 360 – 75 = 285º
Hence, x = 285º
Example 6: In figure AB || CD. Find the value of x.
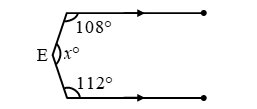
Solution: Draw EF parallel to both AB and CD.
Now, AB || EF and transversal AE cuts them at A and E respectively.
∠BAE + ∠FEA = 180º
⇒ 108º + ∠1 = 180º ⇒ ∠1 = 180º – 108º = 72º
Again, EF || CD and transversal CE cuts them at E and F respectively.
∴ ∠FEC + ∠ECD = 180º
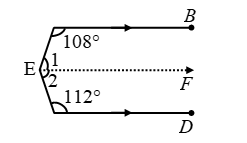
⇒ ∠2 + 112º = 180º
⇒ ∠2 = 180º – 112º
⇒ ∠2 = 68º
Now, x = ∠1 + ∠2
⇒ x = 72º + 68º = 140º
Example 7: In Figure AB || DE. Prove that ∠ABC + ∠BCD = 180º + ∠CDE.
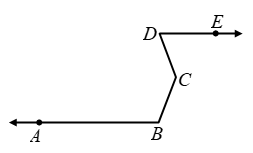
Solution: Through C, draw CF parallel to both AB and DE. Since AB || CF and the transversal BC cuts them at B and C respectively. Therefore,
∠ABC + ∠1 = 180º ….(i)
[∵ conseu. interior angles are supplementary]
Similarly, DE || CF and tranversal CD intersects them at C and D respectively. Therefore,
∠CDE = ∠2 [Alternate angles] ….(ii)
Adding (i) and (ii), we get
∠ABC + ∠1 + ∠2 = 180º + ∠CDE
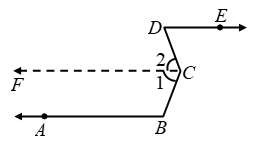
⇒ ∠ABC + ∠BCD = 180º + ∠CDE
[∵ ∠1 + ∠2 = ∠BCD]
Example 8: In Figure PQ || RS, ∠PAB = 70º and ∠ACS = 100º. Determine ∠ABC, ∠BAC and ∠CAQ.
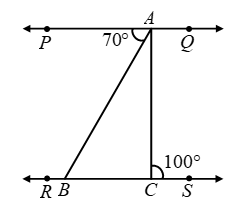
Solution: Since PQ || RS and transversal AB cuts them at A and B respectively.
∴∠ABC = ∠PAB [Alternate angles]
⇒∠ABC = 70º [∵ ∠PAB = 70º (Given)]
Now, PQ || RS and transversal AC cuts them at A and C respectively.
∴∠PAC = ∠ACS [Alternate angles]
⇒∠PAC = 100º [∵ ∠ACS = 100º]
⇒∠PAB + ∠BAC = 100º
[∵ ∠PAC = ∠PAB + ∠BAC]
⇒70º + ∠BAC = 100º
⇒∠BAC = 30º
Now, ray AB stands at A on PQ.
∴∠PAC + ∠CAQ = 180º
⇒100º + ∠CAQ = 180º
⇒∠CAQ = 80º
Hence, ∠ABC = 70º,
∠BAC = 30º and ∠CAQ = 80º.
Example 9: In Figure if ∠2 = 120º and ∠5 = 60º, show that m || n.
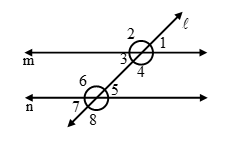
Solution: We have
∠2 = 120º and ∠5 = 60º
But ∠2 = ∠4 [Vertically opposite angles]
∴ ∠4 = 120º, ∠5 = 60º
⇒ ∠4 + ∠5 = 120º + 60º = 180º
⇒ ∠4 and ∠5 are supplementary angles.
⇒ Consecutive interior angles are supplementary.
⇒ m || n.
Example 10: In figure show that AB || EF.
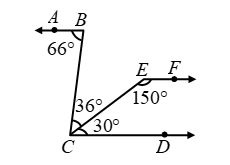
Solution: We have,
∠BCD = ∠BCE + ∠ECD
= 36º + 30º = 66º
∴ ∠ABC = ∠BCD
Thus, lines AB and CD are intersected by the line BC such that ∠ABC = ∠BCD
i.e. the alternate angles are equal. Therefore,
AB || CD ….(i)
Now, ∠ECD + ∠CEF = 30º + 150º = 180º
This shows that the sum of the interior angles on the same side of the transversal CE is 180º
i.e. they are supplementary.
∴ EF || CD ….(ii)
From (i) and (ii), we have
AB || CD and CD || EF ⇒ AB || EF.
Hence, AB || EF
Example 11: In figure given that ∠AOC = ∠ACO and
∠BOD = ∠BDO. Prove that AC || DB.
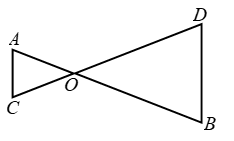
Solution: We have,
∠AOC = ∠ACO and ∠BOD = ∠BDO
But ∠AOC = ∠BOD [Vertically opp. ∠s]
∴ ∠ACO = ∠BOD and ∠BOD = ∠BDO
⇒ ∠ACO = ∠BDO
Thus, AC and BD are two lines intersected by transversal CD such that ∠ACO = ∠BDO i.e. alternate angles are equal. Therefore, AC || DB.
Example 12: In figure AB || DC if x = y and y = z, find the values of x, y and z.
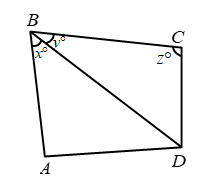
Solution: Since AB || DC and transversal BD intersects them at B and D respectively.
Therefore,
∠ABD = ∠CDB ⇒ ∠CDB = xº
In ΔBCD, we have
yº + zº + xº = 180º
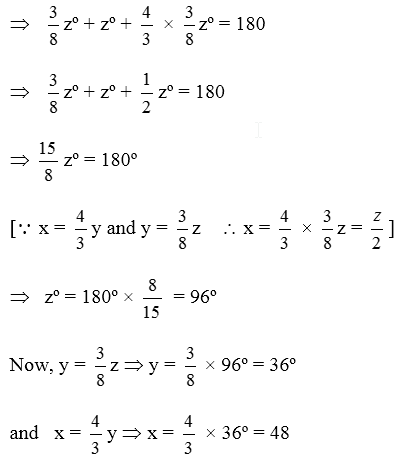
Example 13: In figure lines AB and CD are parallel and P is any point between the two lines. Prove that ∠ABP + ∠CDP = ∠DPB.
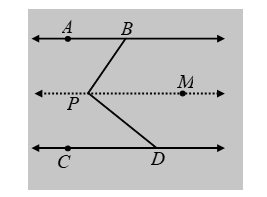
Solution: Through point P draw a line PM parallel to AB or CD.
Now,
PM || AB [By construction]
⇒ ∠ABP = ∠MPB [Alternate angles] ….(i)
It is given that CD || AB and PM || AB by construction. Therefore,
PM || CD
[∵ Lines parallel to the same line are parallel to each other]
⇒ ∠CDP = ∠MPD [Alternate angles] ….(ii)
Adding (i) and (ii), we get
∠ABP + ∠CDP = ∠MPB + ∠MPD = ∠DPB
Example 14: Prove that two lines perpendicular to the same line are parallel to each other.
Solution: Let lines l, m, n be such that l ⊥ n and m ⊥ n as shown in figure.
We have to prove that l|| m
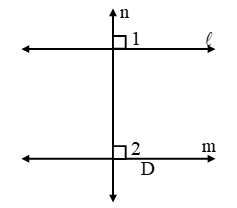
Now,
l ⊥ n and m ⊥ n
⇒ ∠1 = 90º and ∠2 = 90º
⇒ ∠1 = ∠2
Thus, the corresponding angles made by the transversal n with lines l and m are equal.
Hence, l || m.
Example 15: Prove that two angles which have their arms parallel are either equal or supplementary.
Solution: Given : Two angles ∠ABC and ∠DEF such that BA || ED and BC || EF.
To prove: ∠ABC = ∠DEF
or ∠ABC + ∠DEF = 180º
Proof: We have the following three cases:
Case I: When both pairs of arms are parallel in the same sense fig. in this case,
AB || DE and transversal BC cuts them at B and G respectively
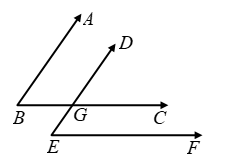
∴∠ABC = ∠DGC …(i)
[Corresponding angles]
Again, BC || EF and transversal DE cuts them at G and E respectively.
∴ ∠DGC = ∠DEF …(ii)
From (i) and (ii), we get
∠ABC = ∠DEF
Case II: When both pairs of arms are parallel in opposite sense in this case,
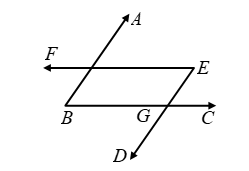
AB || DE and transversal BC cuts them at B and G respectively.
∴ ∠ABC = ∠EGC ….(iii)
[Corresponding angles]
Again, BC || EF and transversal DE cuts them at G and E respectively.
∴ ∠DEF = ∠EGC [Alternate angles] ….(iv)
From (iii) and (iv), we get
∠ABC = ∠DEF.
Case III: When one pair of arms is parallel in the same sense and the other in opposite sense. In this case,
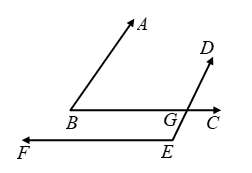
AB || DE and transversal BC cuts them
∴ ∠ABC = ∠BGE [Alternate angles] ….(v)
Again, BC || FE and transversal DE cuts them
∴ ∠DEF + ∠BGE = 180º ….(vi)
[∵ Consecutive interior angles are supplementary]
From (v) and (vi), we get
∠ABC + ∠DEF = 180º
Example 16: In figure bisectors of the exterior angles B and C formed by producing sides AB and AC of ΔABC intersect each other at the point O. Prove that ∠BOC = 90º – 1/2 ∠A.
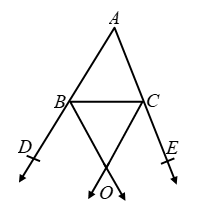
Solution: ∠DBC = 180º – ∠B
Hence, from (i), we have,
∠BOC = 90º – ∠A/2
Example 17: In fig, given that AB || CD.
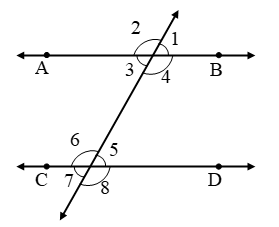
(i) If ∠1 = (120 – x)º and ∠5 = 5xº, find the measures of ∠1 and ∠5.
(ii) If ∠4 = (x + 20)º and ∠5 = (x + 8)º, find the measure of ∠4 and ∠5.
(iii) If ∠2 = (3x – 10)º and ∠8 = (5x – 30)º, determine the measures of ∠2 and ∠8.
(iv) If ∠1 = (2x + y)º and ∠6 = (3x – y)º, determine the measures of ∠2 in terms of y.
(v) If ∠2 = (2x + 30)º, ∠4 = (x + 2y)º and
∠6 = (3y + 10)º, find the measure of ∠5.
(vi) If ∠2 = 2 (∠1), determine ∠7.
(vii)If the ratio of the measures of ∠3 and ∠8 is 4 : 5, find the measure ∠3 and ∠8
(viii)If the complement of ∠5 equals the supplement of ∠4, find the measures of ∠4 and ∠5.
Solution: (i) since ∠1 and ∠5 are the corresponding angles and corresponding angles are equal.
∴ ∠1 = ∠5 ⇒ (120 – x)º = 5xº
⇒ 120º = 6x ⇒ x = 120/6 = 20º
∴ ∠1 = (120 – x)º = (120 – 20)º = 100º
and, ∠5 = 5xº = (5 × 20)º = 100º
(ii) Since ∠4 and ∠5 are consecutive interior angles. Therefore,
∠4 + ∠5 = 180º
[∴ Consecutive interior angles are supplementary]
⇒ (x + 20)º + (x + 8)º = 180º
⇒ 2xº + 28º = 180º ⇒ 2xº = 180º – 28º
⇒ 2x = 152º ⇒ x = 76º
∴ ∠4 = (x + 20)º = (76 + 20)º = 96º
and, ∠5 = (x + 8)º = (76 + 8º) = 84º
(iii) We have,
∠2 = ∠4 [Vertically opposite angles]
and ∠4 = ∠8 [Corresponding angles]
∴ ∠2 = ∠8
⇒ (3x – 10)º = (5x – 30)º ⇒ 3x – 10 = 5x – 30
⇒ 3x – 5x = – 30 + 10 ⇒ – 2x = – 20
⇒ x = 10
∴ ∠2 = (3x – 10)º = (3 × 10 – 10)º = 20º
and ∠8 = (5x – 30)º = (5 × 10 – 30)º = 20º
(iv) Since ∠3 and ∠6 are consecutive interior angles. Therefore
∠3 + ∠6 = 180º
But ∠1 = ∠3 ∴∠1 + ∠6 = 180º
⇒ (2x + y)º + (3x – y)º = 180º
⇒ 5x = 180º ⇒ x = 36.
∴ ∠1 = (2x + y)º = (72 + y)º [∴ x = 36]
But ∠1 + ∠2 = 180º
∴ (72 + y)º + ∠2 = 180º
⇒ ∠2 = (180 – (72 + y))º ⇒ ∠2 = (108 – y)º.
(v) We have,
∠2 = ∠4 [Vertically opposite angles]
and ∠4 = ∠6 [Alternate angles]
∴ ∠2 = ∠4 = ∠6
Now, ∠2 = ∠4
⇒ 2x + 30 = x + 2y ⇒ 2x – x – 2y + 30 = 0
⇒ x – 2y + 30 = 0 ….(1)
And, ∠4 = ∠6 ⇒ (x + 2y) = (3y + 10)
⇒ x – y – 10 = 0 ….(2)
Subtracting (2) from (1), we get
(x – 2y + 30) – (x – y – 10) = 0
⇒ – y + 40 = 0 ⇒ y = 40.
Putting y = 40 in (2), we get x = 50.
∴ ∠4 = (x + 2y)º = (50 + 2 × 40)º = 130º
But ∠4 + ∠5 = 180º
∴ 130º + ∠5 = 180º ⇒ ∠5 = 50º
(vi) We have,
∠1 + ∠2 = 180º [Linear pairs]
∴ ∠2 = 2 ∠1 ⇒ ∠1 + 2 ∠1 = 180º
⇒ 3 ∠1 = 180º ⇒ ∠1 = 60º
But ∠1 = ∠3 [Vertically opposite angles]
∴ ∠3 = 60º
But ∠3 = ∠5 [Alternate angles]
and ∠5 = ∠7 [Vertically opposite angles]
∴ ∠3 = ∠7 ⇒ ∠7 = 60º [∵ ∠3 = 60º]
(vii) We have, ∠3 : ∠8 = 4 : 5. So, let
∠3 = 4x and ∠8 = 5x.
⇒ ∠5 = 4x and ∠8 = 5x
[∵ ∠3 = ∠5 (Alternate angles)]
⇒ ∠5 + ∠8 = 4x + 5x
⇒ 180º = 9x ⇒ x = 20º
∴ ∠3 = 4x = 4 × 20º = 80º
and ∠8 = 5x = 5 × 20º = 100º
(viii) We have, Complement of ∠5 = Supplement of ∠4
⇒ 90º – ∠5 = 180º – ∠4
⇒ 90º – ∠5 = 180º – (180º – ∠5)
[∵ ∠4 + ∠5 = 180º ∴ ∠4 = 180º – ∠5]
⇒ 90º – ∠5 = ∠5
⇒ 2 ∠5 = 90º ⇒ ∠5 = 45º
∴ ∠4 + ∠5 = 180º
⇒ ∠4 + 45º = 180º ⇒ ∠4 = 135º
Example 18: In fig, OP || RS. Determine ∠PQR.
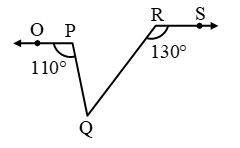
Solution: Produce OP to intersect RQ in a point T.
Now, OT || RS and transversal RT intersect them at T and R respectively.
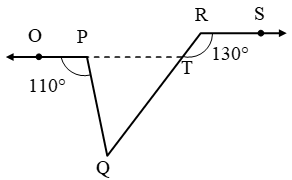
∴ ∠RTP = ∠SRT [Alternate angles]
⇒ ∠RTP = 130º
⇒ ∠PTQ = 180º – 130º = 50º
[∠RTP + ∠PTQ = 180º Linear Pairs]
Since, ray QP stands at P on OT.
∴ ∠OPQ + ∠QPT = 180º
⇒ 110º + ∠QPT = 180º ⇒ ∠QPT = 70º
∴ ∠PQR = 180º – (70º + 50º) = 60º
[∵ Sum of the angles of a triangle is 180º]
Example 19: Prove that through a given point we can draw only one perpendicular to a given line.
Solution: If possible, let PL and PM be two perpendicular from a point P on a line l as shown in fig.
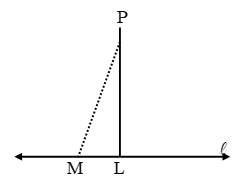
We know that two lines perpendicular to the same line are parallel to each other. Therefore,
PL || PM
But there cannot be two parallel lines passing through the same point. Therefore, through a given point we can draw only one line perpendicular to a given line.
