Parabola
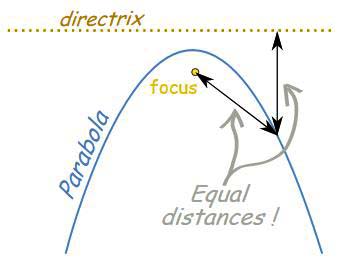
A parabola is the locus of a point which moves in a plane such that its distance from a fixed point (i.e., focus) in the plane is always equal to its distance from a fixed straight line (i.e., directrix) in the same plane.
Standard equation of the parabola
Let S be the focus, ZZ‘ be the directrix of the parabola and be any point on parabola, then standard form of the parabola is y2 = 4ax.
Some other standard forms of parabola are
- Parabola opening to left i.e, y2 = –4ax.
- Parabola opening upwards i.e., x2 = 4ay.
- Parabola opening downwards i.e., x2 = –4ay.
Some terms related to parabola
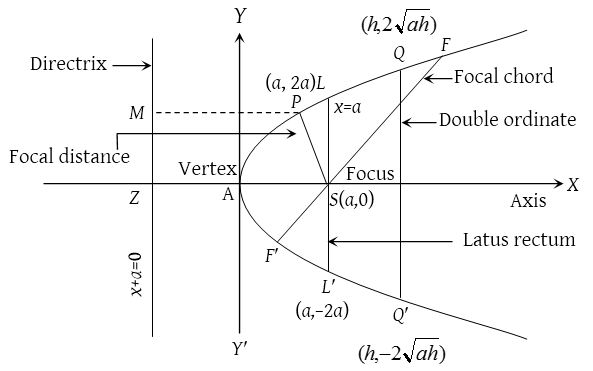
| Important terms | y2 = 4ax | y2 = –4ax | x2 = 4ay | x2 = –4ay |
| Vertex | (0, 0) | (0, 0) | (0, 0) | (0, 0) |
| Focus | (a, 0) | (–a, 0) | (0, a) | (0, –a) |
| Directrix | x = –a | x = a | y = –a | y = a |
| Axis | y = 0 | y = 0 | x = 0 | x = 0 |
| Latusrectum | 4a | 4a | 4a | 4a |
| Focal distance P(x, y) | x + a | a – x | y + a | a – y |
Special form of parabola (y – k)2 = 4a(x – h) = a
The equation of a parabola with its vertex at (h, k) and axis as parallel to x-axis is (y – k)2 = 4a(x – h).
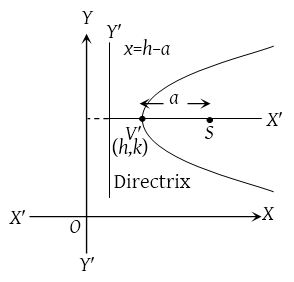If the vertex of the parabola is (p, q) and its axis is parallel to y-axis, then the equation of the parabola is (x – p)2 = 4b(y – q).
Parametric equations of a parabola
| Parabola | y2 = 4ax | y2 = –4ax | x2 = 4ay | x2 = –4ay |
| Parametric Co-ordinates | (at2, 2at) | (–at2, 2at) | (2at , at2) | (2at , –at2) |
| Parametric Equations | x = at2 y = 2at | x = –at2 y = 2at | x = 2at y = at2 | x = 2at y = –at2 |
The parametric equations of parabola (y – k)2 = 4a(x – h) are x = h + at2 and y = k + 2at.
Position of a point and a line with respect to a parabola
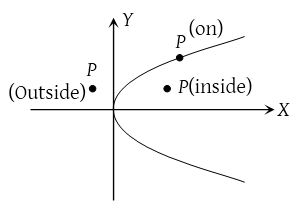
(1) Position of a point with respect to a parabola:
The point P(x1, y1) lies outside, on or inside the parabola y2 = 4ax according as y12 = 4ax1 >, =, < 0.
(2) Intersection of a line and a parabola:
The line y = mx + c does not intersect, touches or intersect a parabola y2 = 4ax, according as >, =, < a/m.
Condition of tangency: The line touches the parabola, if c = a/m.
Equations of tangent in different forms
(1) Point Form
| Equations of tangent of all other standard parabolas at (x1, y1) | |
| Equation of parabola | Tangent at (x1, y1) |
| y2 = 4ax | yy1 = 2a (x + x1) |
| y2 = –4ax | yy1 = –2a (x + x1) |
| x2 = 4ay | xx1 = 2a (y + y1) |
| x2 = –4ay | xx1 = –2a (y + y1) |
(2) Parametric form
| Equations of tangent of all other standard parabolas at ‘t’ | ||
| Equations of parabolas | Parametric coordinates ‘t’ | Tangent at ‘t’ |
| y2 = 4ax | (at2, 2at) | ty = x + at2 |
| y2 = –4ax | (–at2, 2at) | ty = –x + at2 |
| x2 = 4ay | (2at , at2) | tx = y + at2 |
| x2 = –4ay | (2at , –at2) | tx = –y + at2 |
(3) Slope Form
Point of intersection of tangents at any two points on the parabola
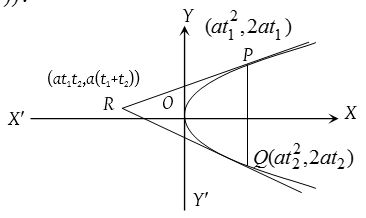
- The point of intersection of tangents at two points P(a1t2, 2at1) and Q(a2t2, 2at2) on the parabola y2 = 4ax is (at1t2, a(t1 + t2)).
- The locus of the point of intersection of tangents to the parabola y2 = 4ax which meet at an angle α is (x + a)2 tan2 α = y2 – 4ax.
- Director circle: The locus of the point of intersection of perpendicular tangents to a conic is known as its director circle. The director circle of a parabola y2 = 4ax is its directrix.
- The tangents to the parabola y2 = 4ax at P(a1t2, 2at1) and Q(a2t2, 2at2) intersect at R. Then the area of triangle PQR is 1/2 a2(t1 – t2)3.
Equation of pair of tangents from a point to a parabola
The combined equation of the pair of the tangents drawn from a point to a parabola is SS’ = T2, where S = y2 – 4ax; S’ = y12 – 4ax1 and T = yy1 – 2a(x + x1)
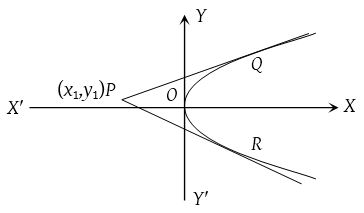The two tangents can be drawn from a point to a parabola. The two tangent are real and distinct or coincident or imaginary according as the given point lies outside, on or inside the parabola.
Equations of normal in different forms
(1) Point form
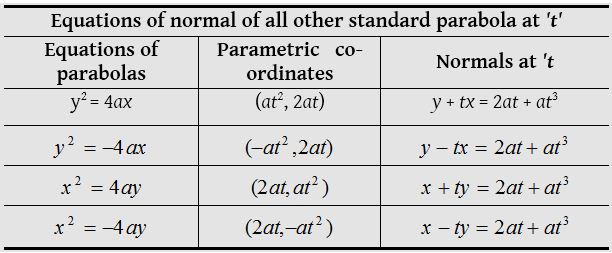
(2) Parametric form
(3) Slope form
