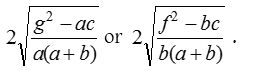What are Pair of Straight Lines?
Equation of pair of straight lines
(1) Equation of a pair of straight lines passing through origin:
The equation ax2 + 2hxy + by2 = 0 represents a pair of straight line passing through the origin where a, h, b are constants.
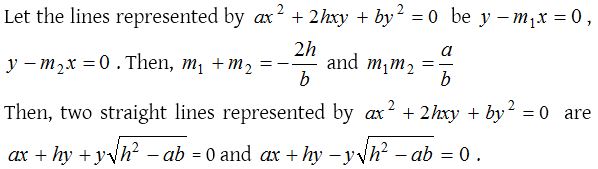
Hence, (a) The lines are real and distinct, if h2 – ab > 0
(b) The lines are real and coincident, if h2 – ab = 0
(c) The lines are imaginary, if h2 – ab < 0
(2) General equation of a pair of straight lines:
An equation of the form, ax2 + 2hxy + by2 + 2gx + 2fy + c = 0
where a, b, c, f, g, h are constants, is said to be a general equation of second degree in x and y.
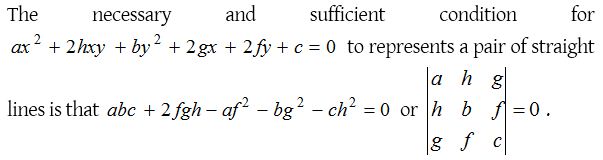
Point of intersection of lines represented by ax2 + 2hxy + by2 + 2gx + 2fy + c = 0
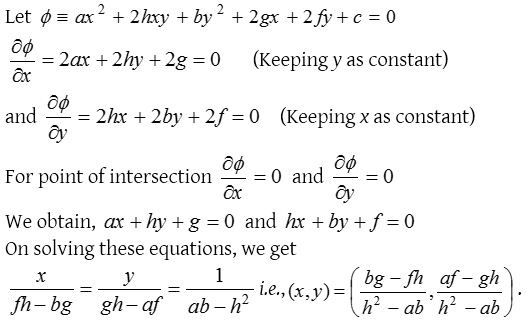
(3) Separate equations from joint equation:
The general equation of second degree be ax2 + 2hxy + by2 + 2gx + 2fy + c = 0
To find the lines represented by this equation we proceed as follows :
Step I: Factorize the homogeneous part ax2 + 2hxy + by2 into two linear factors. Let the linear factors be a’x + b’y and a’’x + b’’y.
Step II: Add constants c’and c’’ in the factors obtained in step I to obtain a’x + b’y + c’ and a’’x + b’’y + c’’. Let the lines be a’x + b’y + c’ = 0 and a’’x + b’’y + c’’ = 0.
Step III: Obtain the joint equation of the lines in step II and compare the coefficients of x, y and constant terms to obtain equations in c’ and c”.
Step IV: Solve the equations in c’ and c” to obtain the values of c’ and c”.
Step V: Substitute the values of c’ and c” in lines in step II to obtain the required lines.
Angle between the pair of lines
The angle between the lines represented by ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 or ax2 + 2hxy + by2 = 0 is given by
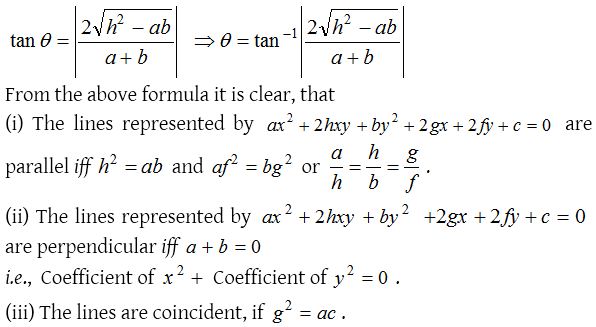
Bisectors of the angles between the lines
(1) The joint equation of the bisectors of the angles between the lines represented by the equation ax2 + 2hxy + by2 = 0 is
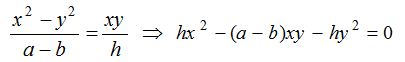
Here, coefficient of x2 + coefficient of y2 = 0. Hence, the bisectors of the angles between the lines are perpendicular to each other. The bisector lines will pass through origin also.
(i) If a = b, the bisectors are x2 – y2 = 0.
i.e., x – y = 0, x + y = 0
(ii) If h = 0, the bisectors are xy = 0 i.e., x = 0, y = 0.
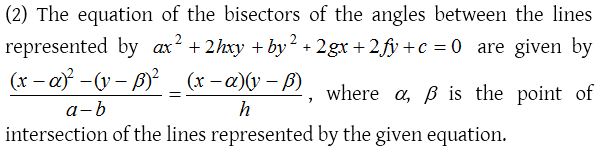
Equation of the lines joining the origin to the points of intersection of a given line and a given curve:
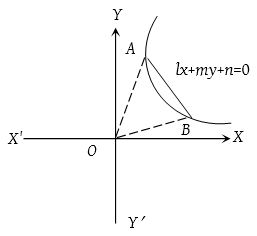The equation of the lines which joins origin to the point of intersection of the line lx + my + n = 0 and curve ax2 + 2hxy + by2 + 2gx + 2fy + c = 0, can be obtained by making the curve homogeneous with the help of line lx + my + n = 0, which is
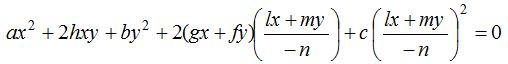
Removal of first degree terms
Let point of intersection of lines represented by ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 …..(i) is (α, β).
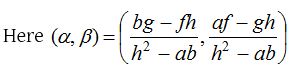
For removal of first degree terms, shift the origin to (α, β) i.e., replacing x by (X + α) and y be (Y + β) in (i).
Alternative Method : Direct equation after removal of first degree terms is
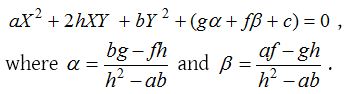
Removal of the term xy from f(X,Y) = ax2 + 2hxy + by2 without changing the origin
Distance between the pair of parallel straight lines
If ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 represents a pair of parallel straight lines, then the distance between them is given by
