One-to-one and Onto Functions
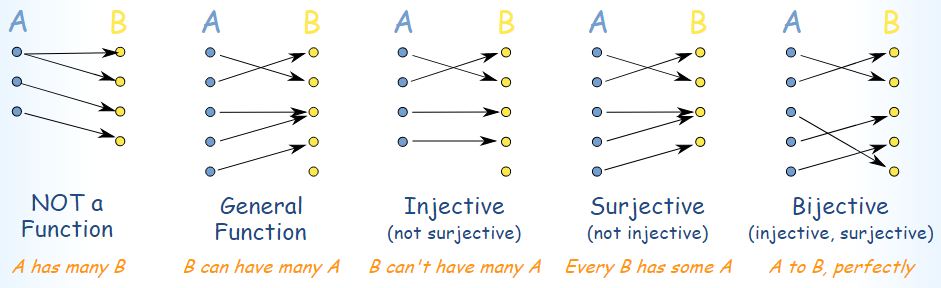
Remember that a function is a set of ordered pairs in which no two ordered pairs that have the same first component have different second components. This means that given any x, there is only one y that can be paired with that x.
Onto Function
A function f from A to B is called onto if for all b in B there is an a in A such that f (a) = b. All elements in B are used.
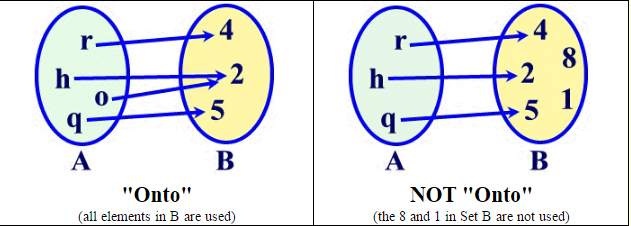
By definition, to determine if a function is ONTO, you need to know information about both set A and B.
When working in the coordinate plane, the sets A and B may both become the Real numbers, stated as f : R→R
Example 1: Is f (x) = 3x – 4 onto where f : R→R
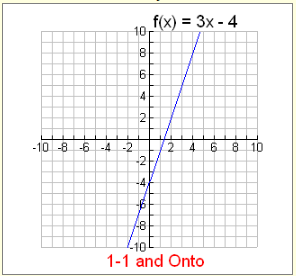
This function (a straight line) is ONTO.
As you progress along the line, every possible y-value is used.
In addition, this straight line also possesses the property that each x-value has one unique y-value that is not used by any other x-element. This characteristic is referred to as being one-to-one.
Example 2: Is g (x) = x² – 2 onto where ?
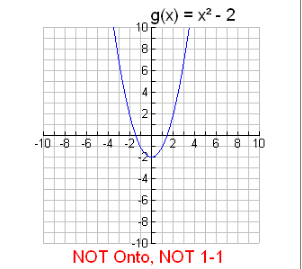
This function (a parabola) is NOT ONTO.
Values less than 2 on the y-axis are never used. Since possible y-values belong to the set of ALL Real numbers, not ALL possible y-values are used.
In addition, this parabola also has y-values that are paired with more than one x-value, such as (3, 7) and (-3, 7).
This function will not be one-to-one.

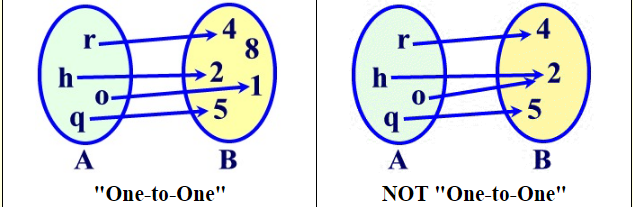
One-to-One Function
A function f from A to B is called one-to-one (or 1-1) if whenever f (a) = f (b) then a = b. No element of B is the image of more than one element in A.
In a one-to-one function, given any y there is only one x that can be paired with the given y. Such functions are referred to as injective.
Example 1: Is f (x) = x³ one-to-one where f : R→R ?
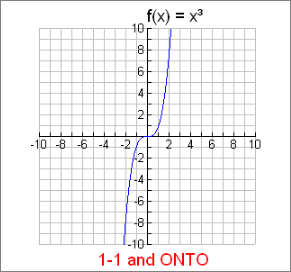
This function is One-to-One.
This cubic function possesses the property that each x-value has one unique y-value that is not used by any other x-element. This characteristic is referred to as being 1-1.
Also, in this function, as you progress along the graph, every possible y-value is used, making the function onto.
Example 2: Is g (x) = | x – 2 | one-to-one where g : R→R
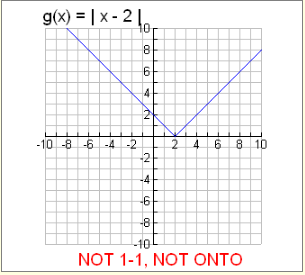
This function is
NOT One-to-One.
This absolute value function has y-values that are paired with more than one x-value, such as (4, 2) and (0, 2).
This function is not one-to-one.
In addition, values less than 0 on the y-axis are never used, making the function NOT onto.
Example 3: Is g (x) = | x – 2 | one-to-one where g : R→[0,∞)
With set B redefined to be , function g (x) will still be NOT one-to-one, but it will now be ONTO.
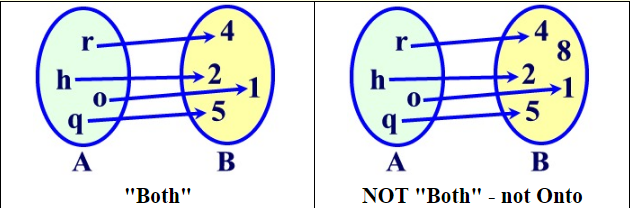
BOTH
Functions can be both one-to-one and onto.
Such functions are called bijective.
Bijections are functions that are both injective and surjective.