NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.2 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.2.
NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.2
Question 1.
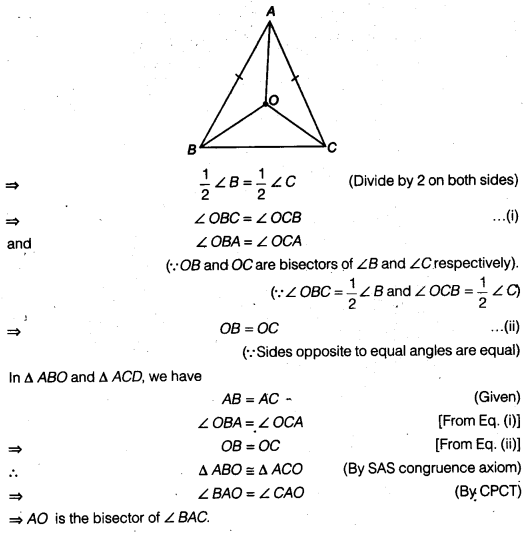
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at 0. Join A to 0. Show that
(i) OB = OC
(ii) AO bisects ∠A
Solution:
(i) In ∆ ABC, we have
AB = AC (Given)
⇒ ∠B = ∠C
(∵ Angles opposite to equal sides are equal)
Question 2.
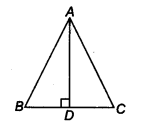
In ∆ ABC, AD is the perpendicular bisector of BC (see figure). Show that ∆ ABC is an isosceles triangle in which AB = AC.
Solution:
In ∆ABD and ∆ACD, we have ,
DB = DC
∠ ADB = ∠ ADC (∵ D bisect SC)
and AD = AD (Common)
∴ ∆ ABD ≅ ∆ACD (By SAS congruence axiom)
⇒ AB = AC (By CPCT)
Renee,∆ ABC is an isosceles triangle.
Question 3.
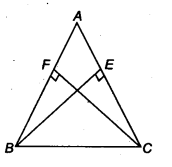
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see figure). Show that these altitudes are equal.
Solution:
In ∆ ABE and ∆ ACF, we have
∠ AEB = ∠ AFC (BE ⊥ AC, CF ⊥ AS, each 90°)
∠ A = ∠ A (Common)
and AS = AC (Given)
∴ ∆ABE ≅ ∆ACF (By AAS congruence axiom)
⇒ BE = CF (By CPCT)
Question 4. .
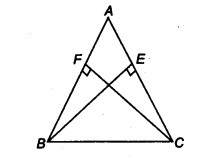
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see figure). Show that
(i) ∆ABE = ∆ACF
(ii) AB = AC i.e., ABC is an isosceles triangle.
Solution:
In ∆ABE and ∆ACF, we have
∠ AEB = ∠ AFC (Each 90°)
∠ BAE = ∠ CAF (Common)
and BE =CF (Given)
∴ ∆ABE ≅ ∆ACF (By AAS congruence axiom)
∴ AB = AC
So, ∆ABC is isosceles.
Question 5.
ABC and DBC are isosceles triangles on the same base BC (see figure). Show that ∠ ABD = ∠ACD.
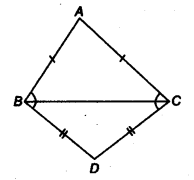
Solution:
In ∆ABC, we have
AB=AC (∵ AABC is an isosceles triangle)
∴ ∠ ABC = ∠ ACB …(i)
(∵ Angles opposite to equal sides are equal)
In ∆ DBC, we have
BD = CD (∵ ADBC is an isosceles triangle)
∴ ∠ DBC = ∠ DCB …(ii)
(∵ Angles opposite to equal sides are equal)
On adding Eqs. (i) and (ii), we have .
∠ ABC + ∠ DBC = ∠ ACB + ∠ DCS
⇒ ∠ ABD = ∠ ACD
Question 6.
∆ABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see figure). Show that ∠ BCD is a right angle.
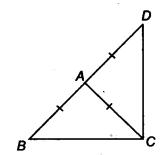
Solution:

Question 7.
ABC is a right angled triangle in which ∠ A = 90° and AB = AC, find ∠ B and ∠ C.
Solution:
We have, ∠A = 90° (Given)
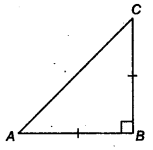
AB = AC (Given)
⇒ ∠B = ∠C
(∵ Angles opposite to equal sides are equal)
Now, we have
∠A+∠B+∠C = 180° (By ∆ property)
90° + ∠B+ ∠B = 180°
⇒ 2 ∠B = 90°
⇒ ∠B = 45°
∴ ∠B = ∠C = 45°
Question 8.
Show that the angles of an equilateral triangle are 60° each.
Solution:
Let ∆ ABC be an equilateral triangle, such that
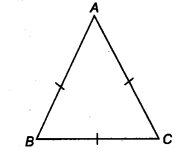
AB = BC = CA (By property)
Now, AB = AC
⇒ ∠B = ∠C …..(i)
(∵Angles opposite to equal sides are equal)
Similarly, CB = CA
⇒∠A = ∠B …(ii)
(∵ Angles opposite to equal sides are equal)
From Eqs. (i) and (ii), we have
∠A=∠B=∠C …(iii)
Now, ∠A+ ∠B+ ∠C = 180° (By ∆ property)
∠A + ∠A + ∠A = 180° [From Eq. (iii)]
3 ∠A = 180°
∠A = 60°
Hence, ∠ A = ∠B = ∠C = 60°
We hope the NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.2 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.2, drop a comment below and we will get back to you at the earliest.
