NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties

NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties, are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties.

NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties

NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties Ex 6.1

Question 1.
In ∆PQR, D is the mid-point of \(\overline { QR } \).

Solution:
\(\overline { PM } \) is the altitude.
PD is the median.
No ! QM ≠ MR.

Question 2.
Draw rough sketches for the following:

(a) In ∆ ABC, BE is a median.
(b) In ∆ PQR, PQ and PR are altitudes of the triangle.
(c) In ∆ XYZ, YL is an altitude in the exterior of the triangle.

Solution:

Question 3.
Verify by drawing a diagram if the median and altitude of an isosceles triangle can be same.
Solution:
AD is the median.
AL is the altitude.

NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties Ex 6.2

Question 1.
Find the value of the unknown exterior angle x in the following diagrams:

Solution:

Question 2.
Find the value of the unknown interior angle x in the following figures:

Solution:

NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties Ex 6.3

Question 1.
Find the value of the unknown x in the following diagrams:

Solution:

Question 2.
Find the values of the unknowns x and y in the following diagrams:

Solution:

NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties Ex 6.4

Question 1.
Is it possible to have a triangle with the following sides?

1. 2 cm, 3 cm, 5 cm
2. 3 cm, 6 cm, 7 cm
3. 6 cm, 3 cm, 2 cm.

Solution:
(i) 2 cm, 3 cm, S cm We have 2 + 3 = 5
⇒ Sum of the lengths of two sides = Length of the third side
This is impossible since the sum of the lengths of any two sides of a triangle is greater than the length of the third side.

(ii) 3 cm, 6 cm, 7 cm
We see that 3 + 6 > 7
6 + 7 > 3
7 + 3 > 6
Therefore, it is possible to have a triangle with side lengths 3 cm, 6 cm, 7 cm.

(iii) 6 cm, 3 cm, 2 cm
We see that 6 + 3 = 9 > 2
3 + 2 = 5 \(\ngtr \) 6
2 + 6 = 8 > 3
Therefore, it is not possible to have a triangle with side lengths 6 cm, 3 cm, 2 cm.

Question 2.
Take any point O in the interior of a triangle PQR. Is

1. OP + OQ > PQ ?
2. OQ + OR > QR?
3. OR + OP > RP ?

Solution:

1. Yes ! OP + OQ > PQ …(1)
   Sum of the lengths of any two sides of a triangle is greater than the length of the third side
2. Yes ! OQ + OR > QR …(2)
   Sum of the lengths of any two sides of a triangle is greater than the length of the third side
3. Yes ! OR + OP > RP …(3)
   Sum of the lengths of any two sides of a triangle is greater than the length of the third side

Question 3.
AM is a median of a triangle ABC. Is AB + BC + CA > 2 AM?
(Consider the sides of triangles ∆ ABM and ∆ AMC.)

Solution:
In ∆ ABM, AB + BM > AM …(1)
Sum of the lengths of any two sides of a triangle is greater than the length of the third side
In ∆ ACM,
CA + CM > AM …(2)
Sum of the lengths of any two sides of a triangle is greater than the length of the third side
Sum (1) and (2),
(AB + BM) + (CA + CM) > AM + AM
⇒ AB + (BM + CM) + CA > 2 AM
⇒ AB + BC + CA > 2 AM.

Question 4.
ABCD is a quadrilateral.
Is AB + BC + CD + DA > AC + BD ?

Solution:
In ∆ ABC, AB + BC > AC …(1)
Sum of the lengths of any two sides of a triangle is greater than the length of the third side
In ∆ ACD, CD + DA > AC …(2)
Sum of the lengths of any two sides of a triangle is greater than the length of the third side
Adding (1) and (2),
AB + BC + CD + DA > 2AC …(3)
In ∆ ABD, AB + DA > BD …(4)
Sum of the lengths of any two sides of a triangle is greater than the length of the third side
In ∆ BCD, BC + CD > BD …(5)
Sum of the lengths of any two sides of a triangle is greater than the length of the third side
Adding (4) and (5),
AB + BC + CD + DA > 2BD …(6)
Adding (3) and (6),
2 [AB + BC + CD + DA] > 2 (AC + BD)
⇒ AB + BC + CD + DA > AC + BD.

Question 5.
ABCD is a quadrilateral. Is AB + BC + CD + DA < 2 (AC + BD)?

Solution:
In ∆ OAB, OA + OB > AB ….(1)
Sum of the lengths of any two sides of a triangle is greater than the length of the third side.
In ∆ OBC, OB + OC > BC ….(2)
Sum of the lengths of any two sides of a triangle la greater than the length of the third side.
In ∆ OCA,OC + OA > CA ….(3)
Sum of the lengths of any two sides of a triangle is greater than the length of the third side
In ∆ OAD, OA + OD > AD ….(4)
Sum of the lengths of any two sides of a triangle is greater than the length of the third side
Adding (1), (2), (3) and (4),
2(OA + OB + OC + OD) > AB + BC + CD + DA
⇒ AB + BC + CD + DA < 2 (OA + OB + OC + OD)
⇒ AB + BC + CD + DA < 2(OA + OC + OB + OD)
⇒ AB + BC + CD + DA < 2 (AC + BD).

Question 6.
The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?
Solution:
Let x cm be the length of the third side.
∴ Sum of the lengths of any two sides of a triangle is greater than the length of the third side.
∴ We should have

∴ The length of the third side should be any length between 3 cm and 27 cm.

NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties Ex 6.5

Question 1.
PQR is a triangle right-angled at P. If PQ = 10 cm and PR = 24 cm, find QR.

Solution:
QR² = 10² + 24² By Pythagoras Property
⇒ = 100 + 576 = 676
⇒ QR = 26 cm.

Question 2.
ABC is a triangle right-angled at C. If AB – 25 cm and AC = 7 cm, find BC.

Solution:
AC² + BC² = AB² By Pythagoras Property
⇒ 7² + BC² = 25²
⇒ 49 + BC² = 625
⇒ BC² = 625 – 49
⇒ BC² = 576
⇒ BC = 24 cm.

Question 3.
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.

Solution:
Let the distance of the foot of the ladder from the wall be a m. Then,

Hence, the distance of the foot of the ladder from the wall is 9 m.

Question 4.
Which of the following can be the sides of a right triangle ?

1. 2.5 cm, 6.5 cm, 6 cm.
2. 2 cm, 2 cm, 5 cm.
3. 1.5 cm, 2 cm, 2.5 cm.

In the case of right-angled triangles, identify the right angles.
Solution:
(i) 2.5 cm, 6.5 cm, 6 cm We see that
(2.5)² + 6² = 6.25 + 36 = 42.25 = (6.5)²
Therefore, the given lengths can be the sides of a right triangle. Also, the angle between the lengths, 2.5 cm and 6 cm is a right angle.

(ii) 2 cm, 2 cm, 5 cm
∵ 2 + 2 = 4 \(\ngtr\) 5
∴ The given lengths cannot be the sides of a triangle
The sum of the lengths of any two sides of a triangle is greater than the third side

(iii) 1.5 cm, 2 cm, 2.5 cm We find that
1.5² + 2² = 2.25 + 4 = 6.25 = 2.5²
Therefore, the given lengths can be the sides of a right triangle. Also, the angle between the lengths 1.5 cm and 2 cm is a right angle.

Question 5.
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
Solution:
AC = CD Given
In right angled triangle DBC, DC² = BC² + BD²
by Pythagoras Property = 5² + 12² = 25 + 144 = 169

⇒ DC = 13 ⇒ AC = 13
⇒ AB = AC + BC = 13 + 5 = 18
Therefore, the original height of the tree = 18 m.

Question 6.
Angles Q and R of a ∆ PQR are 25° and 65°. Write which of the following is true :

(i) PQ² + QR² = RP²
(ii) PQ² + RP² = QR²
(iii) RP² + QR² = PQ²
Solution:
(ii) PQ² + RP² = QR² is true.

Question 7.
Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.

Solution:
In right-angled triangle DAB, AB² + AD² = BD²
⇒ 40² + AD² = 41² ⇒ AD² = 41² – 40²
⇒ AD² = 1681 – 1600
⇒ AD² = 81 ⇒ AD = 9
∴ Perimeter of the rectangle
= 2(AB + AD) = 2(40 + 9) = 2(49) = 98 cm
Hence, the perimeter of the rectangle is 98 cm.

Question 8.
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.

Solution:
Let ABCD be a rhombus whose diagonals BD and AC are of lengths 16 cm and 30 cm respectively. Let the diagonals BD and AC intersect each other at O.
Since the diagonals of a rhombus bisect each other at right angles. Therefore
BO = OD = 8 cm,
AO = OC = 15 cm,
∠AOB = ∠BOC
= ∠COD = ∠DOA = 90°
In right-angled triangle AOB.
AB² = OA² + OB²
By Pythagoras Property
⇒ AB² = 15² + 8²
⇒ AB² = 225 + 64
⇒ AB² = 289
⇒ AB = 17cm
Therefore, perimeter of the rhombus ABCD = 4 side = 4 AB = 4 × 17 cm = 68 cm
Hence, the perimeter of the rhombus is 68 cm.

NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties MCQ

Important Multiple Choice Questions

1. How many elements are there in a triangle?

(a) 3
(b) 6
(c) 4
(d) None of these.

2. How many vertices does a triangle have?

(a) 1
(b) 2
(c) 3
(d) 4.

3. How many sides are there in a triangle?

(a) 1
(b) 2
(c) 3
(d) 4.

4. How many angles are there in a triangle?

(a) 1
(b) 2
(c) 3
(d) 4.

5. If two sides of a triangle are not equal, the triangle is called

(a) scalene
(b) isosceles
(c) equilateral
(d) right-angled.

6. If two sides of a triangle are equal, the triangle is called

(a) isosceles
(b) equilateral
(c) scalene
(d) right-angled.

7. If all the three sides of a triangle are equal, the triangle is called

(a) equilateral
(b) right-angled
(c) isosceles
(d) scalene.

8. If all the angles of a triangle are acute, the triangle is called

(a) obtuse-angled
(b) acute-angled
(c) right-angled
(d) none of these.

9. If one angle of a triangle measures 90°, the triangle is called

(a) acute-angled
(b) obtuse-angled
(c) right-angled
(d) none of these.

10. If one angle of a triangle is obtuse, the triangle is called

(a) acute-angled
(b) obtuse-angled
(c) right-angled
(d) none of these.

11, How many medians can a triangle have?

(a) 1
(b) 2
(c) 3
(d) 4

12. How many altitudes can a triangle have?

(a) 1
(b) 2
(c) 3
(d) 4.

13. The total measure of the three angles of a triangle is

(a) 360°
(b) 90°
(c) 180°
(d) none of these.

14. The measure of each angle of an equilateral triangle is

(a) 30°
(b) 45°
(c) 90°
(d) 60°.

15. Which of the following statements is true?

(a) A triangle can have two right angles
(b) A triangle can have two obtuse angles
(c) A triangle can have two acute angles
(d) A triangle can have all the three angles less than 60°.

16. Which of the following statements is true?

(a) A triangle can have all the three angles equal to 60°.
(b) A triangle can have all the three angles greater than 60°.
(c) The sum of any two angles of a triangle is always greater than the third angle.
(d) The difference between the lengths of any two sides of a triangle is greater than the length of the third side.

17. Which of the following statement is false?

(a) The sum of the lengths of any two sides of a triangle is less than the third side.
(b) In a right-angled triangle, the square on the hypotenuse = sum of the squares on the legs.
(c) If the Pythagorean property holds, the triangle must be right-angled.
(d) The diagonal of a rectangle produce ‘by itself the same area as produced by its length and breadth.

18. Two angles of a triangle measure 90° and 30°. The measure of the third angle is

(a) 90°
(b) 30°
(c) 60°
(d) 120°.

19. The ratio of the measures of the three angles of a triangle is 2 : 3 : 4. The measure of the largest angle is

(a) 80°
(b) 60°
(c) 40°
(d) 180°.

20. In the following figure, the side BC of ∆ ABC is extended up to the point D. If ∠ A = 55° and ∠ B = 60°, then the measure of ∠ACD is

(a) 120°
(b) 110°
(c) 115°
(d) 125°.

21. In the following figure, the measure of ∠A is

(a) 30°
(b) 45°
(c) 90°
(d) 30°.

22. In the following figure, the measure of ∠A is

(a) 70°
(b) 90°
(c) 80°
(d) 100°.

23. In the following figure, m || QR. Then, the measure of ∠QPR is

(a) 80°
(b) 85°
(c) 75°
(d) 70°.

24. In the following figure, find ∠ x and ∠ y, if ∠x – ∠y – 10°

(a) 65°, 55°
(b) 55°, 45°
(c) 45°, 35°
(d) 60°, 60°.

25. In the following figure, find ∠ B.

(a) 30°
(b) 45°
(c) 40°
(d) 60°

26. In the following figure, ∆ ABC is an equilateral triangle. Find ∠x.

(a) 30°
(b) 45°
(c) 60°
(d) 90°

27. In the following figure, one angle of triangle ABC is 40°. If the difference of the other two angles is 30°, find the larger of the other two angles.

(a) 85°
(b) 80°
(c) 75°
(d) 70°.

28. In the following figure, find

(a) 60°
(b) 70°
(c) 80°
(d) 75°.

29. In the following figure, find x if BA || CE.

(a) 60°
(b) 40°
(c) 45°
(d) 65°

30. Find the value of the unknown interior angle x in the following figure:

(a) 30°
(b) 35°
(c) 40°
(d) 45°

31. Find the value of unknown x in the following figure:

(a) 40°
(b) 50°
(c) 45°
(d) 55°

32. Find the value of unknown x in the following figure:

(a) 10°
(b) 15°
(c) 20°
(d) 25°

33. Find angle x in the following figure:

(a) 90°
(b) 80°
(c) 95°
(d) 100°

34. Find angle x in the following figure:

(a) 40°
(b) 50°
(c) 45°
(d) 60°

35. Find angle x in the following figure:

(a) 40°
(b) 30°
(c) 25°
(d) 35°

36. Find angle x in the following figure:

(a) 40°
(b) 45°
(c) 35°
(d) 50°

37. Find angle x in the following figure:

(a) 58°
(b) 59°
(c) 57°
(d) 56°

38. Find angle x in the following figure:

(a) 45°
(b) 40°
(c) 35°
(d) 50°

39. In which case of the following lengths of sides of a triangle, is it possible to draw a triangle?

(а) 3 cm, 4 cm, 7 cm
(b) 2 cm, 3 cm, 7 cm
(c) 3 cm, 4 cm, 5 cm
(d) 3 cm, 3 cm, 7 cm.

40. Which of the following cannot be the sides of a right triangle?

(а) 2 cm, 2 cm, 4 cm
(b) 5 cm, 12 cm, 13 cm
(c) 6 cm, 8 cm, 10 cm
(d) 3 cm, 4 cm, 5 cm.

ANSWERS

HINTS/SOLUTIONS

1. See a triangle.
2. See a triangle.
3. See a triangle.
4. See a triangle.
5. Definition of a scalene triangle.
6. Definition of an isosceles triangle.
7. Definition of an equilateral triangle.
8. Definition of an acute-angled triangle.
9. Definition of a right triangle.
10. Definition of an obtuse angled triangle.
11. Draw medians and count.
12. Draw altitudes and count.
13. Angle Sum Property of a triangle.
14. x° + x° + x° = 180° ⇒ x° = 60°.
18. Third angle = 180° – (90° + 30°) = 60°.
19. Largest angle = 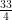 × 180° = 80°.
20. ∠ ACD = 60° + 55° = 115°.
21. ∠ A – 180° – [(180° – 120°) + (180° – 120°)] = 60°.
22. ∠A – 180° – (60° + 40°) = 80°
23. ∠ PQR = 50°
∴ ∠ QPR – 180° – (50° + 45°) = 85°.
24. ∠x + ∠y = 120°; ∠x – ∠y = 10° Solve to get ∠x = 65°, ∠y = 55°.
25. ∠B = 180° – [(180° – 110°) + 50°] = 60°.
26. ∠ABC = 60°.
∴ ∠ABD = 180° – 60° = 120°
∴ x = 180° – (120° + 30°) = 30°.
27. x + y = 180° – 40° = 140° x – y = 30°. Solve to get x = 85°.
28. x + x = 140° ⇒ x = 70°.
29. ∠ECD = ∠ABC = 50°;
∴ x = 180° – (65° + 50°) = 65°.
30. x + 90° = 130° ⇒ x = 40°.
31. x + 40° + 90° = 180° ⇒ x = 50°.
32. x + 5x + 90° = 180° ⇒ x = 15°.
33. x + 45 + 45° = 180° ⇒ x = 90°.
34. x = 50°.
35. x + x + 120° = 180° ⇒ x = 30°.
36. x + 140° = 180° ⇒ x = 40°.
37. x + x = 116° ⇒ x = 58°.
38. x = 45°.
39. 3 + 4 > 5; 4 + 5 > 3; 5 + 3 > 4.
40. 2² + 2² = 8; 4² = 16
∴ 2² + 2² ≠ 4²

We hope the NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties, help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties, drop a comment below and we will get back to you at the earliest.