NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.4 - A Plus Topper.com

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.4 are part of NCERT Solutions for Class 10 Maths. Here are we have given Chapter 8 Introduction to Trigonometry Class 10 NCERT Solutions Ex 8.4.

• Introduction to Trigonometry Class 10 Ex 8.1
• Introduction to Trigonometry Class 10 Ex 8.2
• Introduction to Trigonometry Class 10 Ex 8.3

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.4

NCERT Solutions for Class 10 Maths

Page No : 193

Question 1. Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.

Solution:

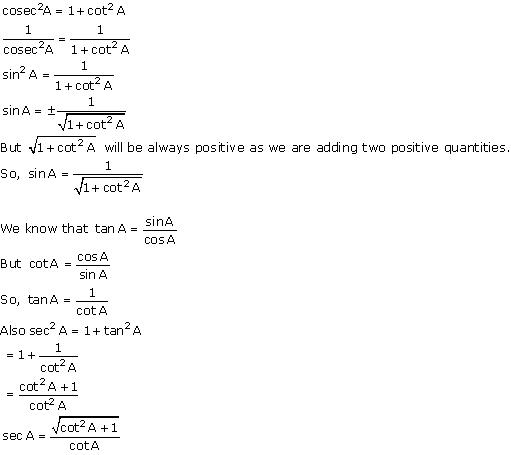
Question 2. Write all the other trigonometric ratios of ∠A in terms of sec A.

Solution:

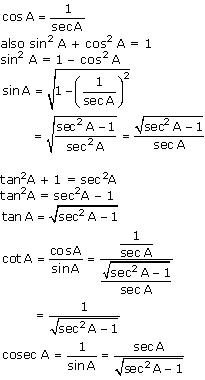
Question 3. Evaluate :
(i) \(\frac { { sin }^{ 2 }{ 63 }^{ 0 }+{ sin }^{ 2 }{ 27 }^{ 0 } }{ { cos }^{ 2 }{ 17 }^{ 0 }+{ cos }^{ 2 }{ 73 }^{ 0 } } \)
(ii) sin 25° cos 65° + cos 25° sin 65°

Solution:

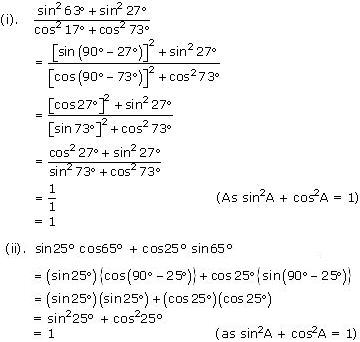
Question 4. Choose the correct option. Justify your choice.
(i) 9 sec²A – 9 tan²A =
(A) 1 (B) 9 (C) 8 (D) 0

(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ)
(A) 0 (B) 1 (C) 2 (D) – 1

(iii) (secA + tanA) (1 – sinA) =
(A) secA (B) sinA (C) cosecA (D) cosA

(iv) \(\frac { 1+{ tan }^{ 2 }A }{ 1+{ cot }^{ 2 }A } =\)
(A) sec²A (B) -1 (C) cot²A (D) tan²A

Solution:
(i) 9sec2A – 9tan2A
= 9(sec2A – tan2A)
= 9 (1)            [as sec2 A – tan2 A = 1]
= 9
Hence alternative (B) is correct.

(ii) (1 + tanθ + secθ) (1 + cotθ – cosecθ)

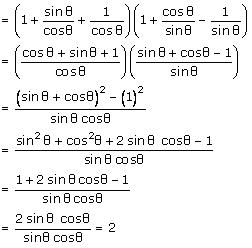
Hence alternative (C) is correct.

(iii) (secA + tanA) (1 – sinA)

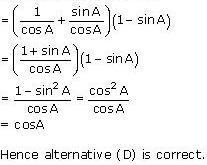
(iv) \(\frac { 1+{ tan }^{ 2 }A }{ 1+{ cot }^{ 2 }A } =\)

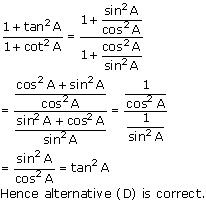
Question 5. Prove the following identities, where the angles involved are acute angles for which the
expressions are defined.
(i) \(\left( cosec\theta -cot\theta \right) ^{ 2 }=\frac { 1-cos\theta }{ 1+cos\theta } \)
(ii) \(\frac { cosA }{ 1+sinA } +\frac { 1+sinA }{ cosA } =2secA\)
(iii) \(\frac { tan\theta }{ 1-cot\theta } +\frac { cot\theta }{ 1-tan\theta } =1+sec\theta cosec\theta \)
(iv) \(\frac { 1-secA }{ secA } =\frac { { sin }^{ 2 }A }{ 1-cosA } \)
(v) \(\frac { cosA-sinA+1 }{ cosA+sinA-1 } =cosecA+cotA\) using the identity cosec²A = 1+cot²A.
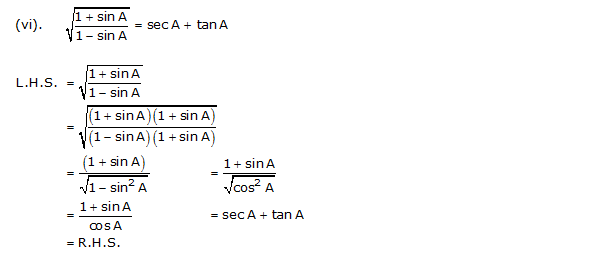
(vi) \(\sqrt { \frac { 1+sinA }{ 1-sinA } } =\quad secA+tanA\)
(vii) \(\frac { sin\theta -{ 2sin }^{ 3 }\theta }{ { 2cos }^{ 3 }\theta -cos\theta } =tan\theta \)
(viii) (sin A + cosec A)² + (cos A + sec A)² = 7+tan²A+cot²A
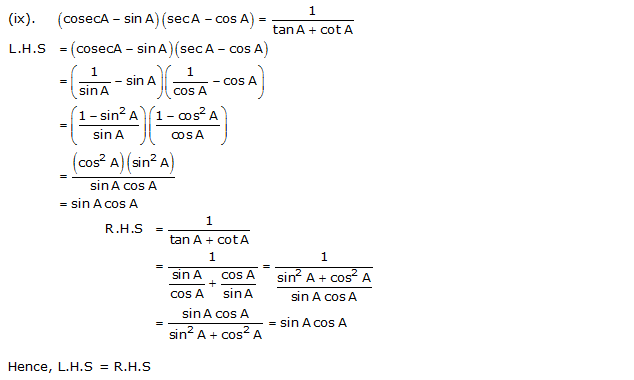
(ix) \(\left( cosecA-sinA \right) \left( secA-cosA \right) =\frac { 1 }{ tanA+cotA } \)
(x) \(\left( \frac { 1+{ tan }^{ 2 }A }{ 1+cot^{ 2 }A } \right) ^{ 2 }=\left( \frac { 1-{ tan }A }{ 1-cotA } \right) ^{ 2 }={ tan }^{ 2 }A\)

Solution:

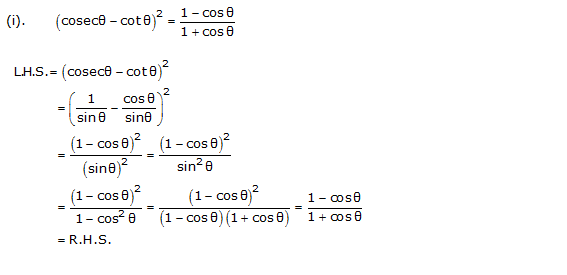
(v) \(\frac { cosA-sinA+1 }{ cosA+sinA-1 } =cosecA+cotA\) using the identity cosec²A = 1+cot²A.

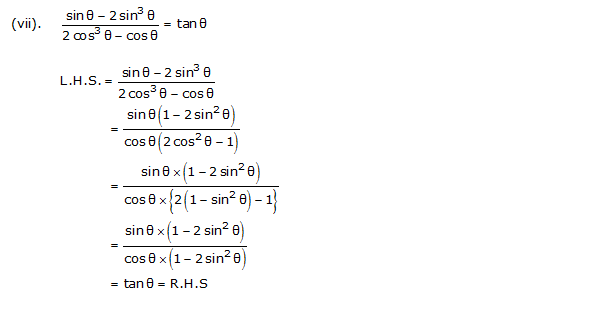
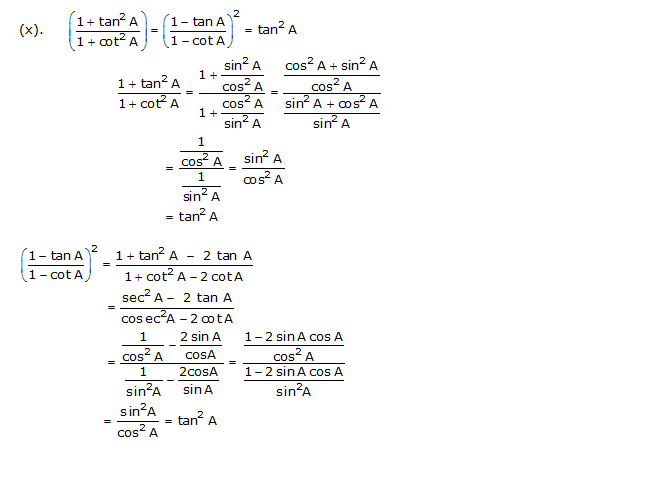
We hope the NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.4 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.4, drop a comment below and we will get back to you at the earliest.