NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.4 are part of NCERT Solutions for Class 10 Maths. Here are we have given Chapter 7 Coordinate Geometry Class 10 NCERT Solutions Ex 7.4.
- Coordinate Geometry Class 10 Ex 7.1
- Coordinate Geometry Class 10 Ex 7.2
- Coordinate Geometry Class 10 Ex 7.3
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 7 |
| Chapter Name | Coordinate Geometry |
| Exercise | Ex 7.4 |
| Number of Questions Solved | 8 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.4
NCERT Solutions for Class 10 Maths
Question 1.Determine the ratio in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, – 2) and B(3, 7).
Solution:
If the ratio in which P divides AB is k : 1, then the coordinates of the point P will be
\(\frac { k{ x }_{ 2 }+{ x }_{ 1 } }{ k+1 } ,\frac { k{ y }_{ 2 }+{ y }_{ 1 } }{ k+1 } \)
Let the given line divides the line segment joining the points A (2, – 2) and B (3, 7) in a ratio k: 1.
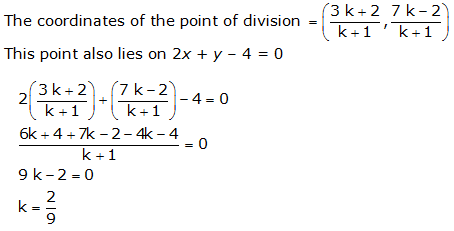
Question 2. Find a relation between x and y if the points (x, y), (1, 2) and (7, 0) are collinear.
Solution:
If the given points are collinear the area of triangle formed by these points will be O.
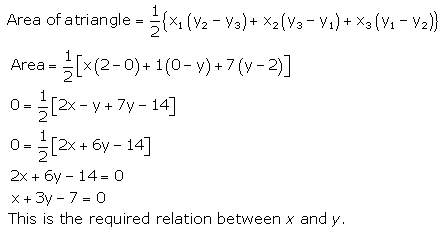
Question 3. Find the centre of a circle passing through the points (6, – 6), (3, – 7) and (3, 3).
Solution:
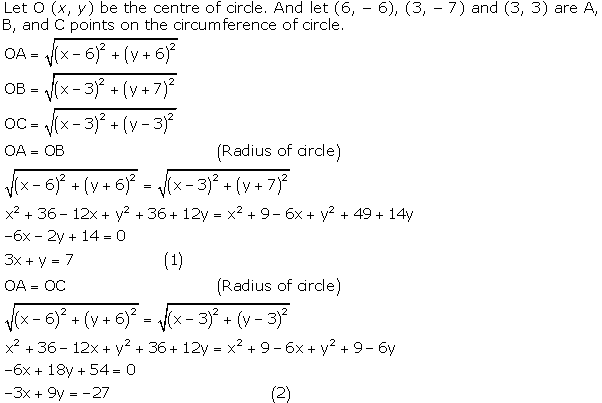
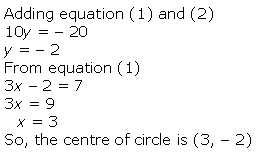
Question 4. Find two opposite vertices of a square are (—1, 2) and (3, 2), find the coordinates of the other two vertices.
Solution:
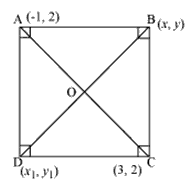
Let ABCD be a square having (—1, 2), (3, 2) as vertices A and C respectively and (x, y), (x1, y1) be the coordinate of vertex B and D respectively.
We know that are sides of a square are equal to each other AB = BC
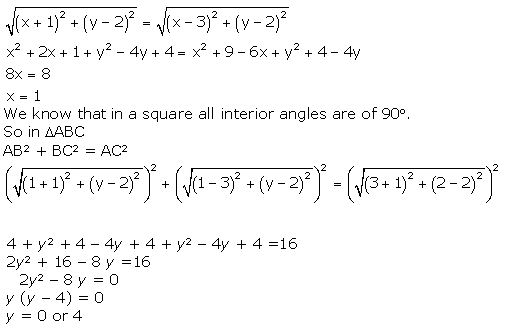
We know that in a square diagonals are of equal length and bisect each other at 900 Let O be the mid point of AC so it will also be the mid point of BD.

Question 5. The class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is a
triangular grassy lawn in the plot as shown in the Figure the students are to sow seeds of flowering plants on the remaining area of the plot.
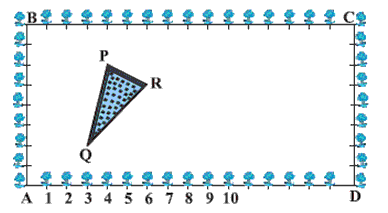
(i) Taking A as origin, find the coordinates of the vertices of the triangle.
(ii) What will be the coordinates of the vertices of ∆PQR if C is the origin?
Also calculate the areas of the triangles in these cases. What do you observe?
Solution:

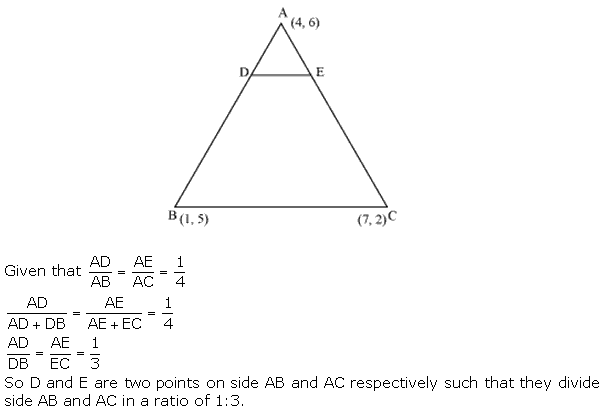
Question 6. The vertices of a MBC are A (4, 6), B (1, 5) and C (7, 2), A line is drawn to intersect sides AB and AC at D and E respectively, such that \(\frac { AD }{ AB } =\frac { AE }{ AC } =\frac { 1 }{ 4 } \)
Calculate the area of the ∆ADE and compare it with the area of ∆ABC.
Solution:
Coordinates of the point P(x, y) which divides the line segment joining the points A(x1, y1) and B(x2,y2) intenally in the ratio m1 : m2, are
\(\frac { { m }_{ 1 }{ x }_{ 2 }+{ m }_{ 2 }{ x }_{ 1 } }{ { m }_{ 1 }+{ m }_{ 2 } } ,\frac { { m }_{ 1 }{ y }_{ 2 }+{ m }_{ 2 }{ y }_{ 1 } }{ { m }_{ 1 }+{ m }_{ 2 } } \)
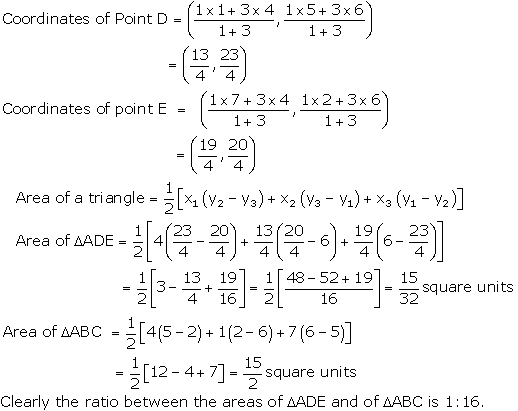
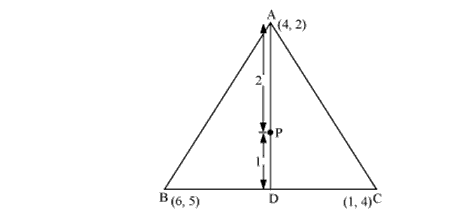
Question 7. Let A (4, 2), B (6, 5) and C (1, 4) be the vertices of ∆ABC.
(i) The median from A meets BC at D. Find the coordinates of point D.
(ii) Find the coordinates of the point P on AD such that AP: PD = 2: 1
(iii) Find the coordinates of point Q and R on medians BE and CF respectively.
Such that BQ: QE = 2:1 and CR: RF = 2:1,
(iv) What do you observe?
(v) If A(x1, y1), B(x2, y2), and C(x3, y3) are the vertices of ∆BC, find the coordinates of the centroid of the triangle.
Solution:
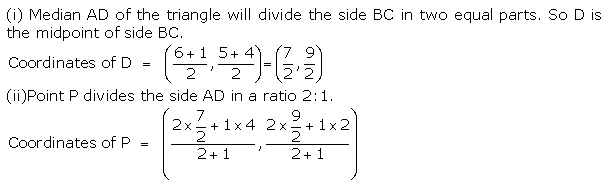
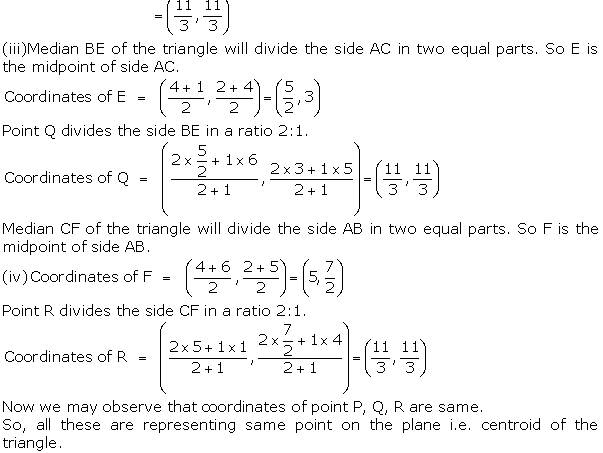
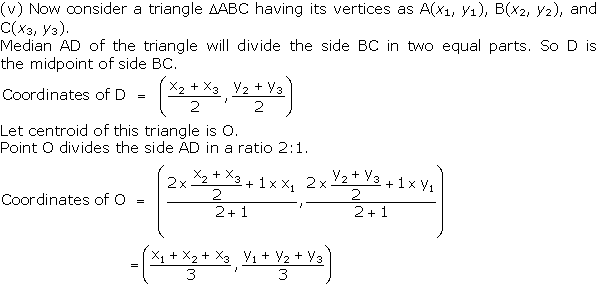
Note: Coordinates of the point P(x, y) which divides the line segment joining the points A(x1, y1) and B(x2,y2) intenally in the ratio m1 : m2, are
\(\frac { { m }_{ 1 }{ x }_{ 2 }+{ m }_{ 2 }{ x }_{ 1 } }{ { m }_{ 1 }+{ m }_{ 2 } } ,\frac { { m }_{ 1 }{ y }_{ 2 }+{ m }_{ 2 }{ y }_{ 1 } }{ { m }_{ 1 }+{ m }_{ 2 } } \)
Question 8. ABCD is a rectangle formed by the points A (-1,-1), B (—1 4), C (5, 4) and D (5,—1). P, Q, R and S are the mid-points of AB, BC, CD, and DA respectively. Is the quadrilateral PQRS ¡s a square? a rectangle? Or a rhombus? Justify your answer.
Solution:
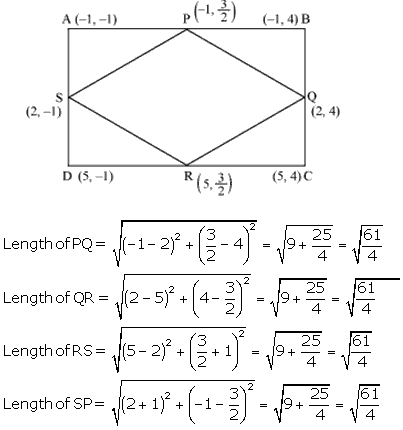
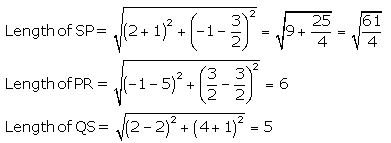
Here all sides of given quadrilateral is of same measure but the diagonals are of different lengths. So, PQRS is a rhombus.
We hope the NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.4 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.4, drop a comment below and we will get back to you at the earliest.
