NCERT Solution for Class 10 Maths Chapter 6 Triangles Ex 6.6

NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.6 are part of NCERT Solutions for Class 10 Maths. Here are we have given Chapter 6 Triangles Class 10 NCERT Solutions Ex 6.6.

Board	CBSE
Textbook	NCERT
Class	Class 10
Subject	Maths
Chapter	Chapter 6
Chapter Name	Triangles
Exercise	Ex 6.6
Number of Questions Solved	10
Category	NCERT Solutions

NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.6

NCERT Solutions for Class 10 Maths

Question 1. In the given figure, PS is the bisector of ∠QPR of ∆PQR. Prove that

Solution:

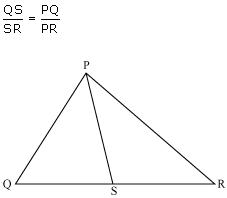
Let us draw a line segment RT parallel to SP which intersects extended line segment QP at point T.

NCERT Solutions for Class 10 Maths Chapter 6 Triangles 109

Question 2. In the given figure, D is a point on hypotenuse AC of ∆ABC, DM ⊥ BC and DN ⊥ AB, Prove that:

(i). DM² = DN.MC
(ii). DN² = DM.AN

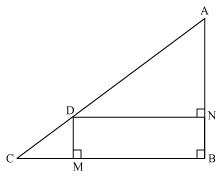
Solution:
(i). Let us join DB.

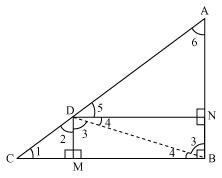
DN || CB
DM || AB
So, DN = MB
DM = NB
The condition to be proved is the case when DNBM is a square or D is the midpoint of side AC.
Then ∠CDB = ∠ADB = 90°
∠2 + ∠3 = 90°       (1)
In ∆CDM
∠ 1 + ∠ 2 + ∠ DMC = 180°
∠ 1 + ∠ 2 = 90°       (2)
In ∆DMB
∠ 3 + ∠ DMB + ∠ 4 = 180°
∠ 3 + ∠ 4 = 90°       (3)
From equation (1) and (2)
∠ 1 = ∠ 3
From equation (1) and (3)
∠ 2 = ∠ 4
∆BDM ~ ∆ DCM

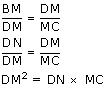
(ii). Similarly in ∆DBN
∠ 4 + ∠ 3 = 90°           (4)
In ∆DAN
∠ 5 + ∠ 6 = 90°           (5)
In ∆DAB
∠4 + ∠ 5 = 90°           (6)
From equation (4) and (6)
∠3 = ∠ 5
From equation (5) and (6)
∠4 = ∠ 6
∆DNA   ~ ∆BND

Question 3. In the given figure, ABC is a triangle in which ∠ ABC> 90° and AD ⊥ CB produced.

Prove that AC² = AB² + BC² + 2BC . BD.

Solution:
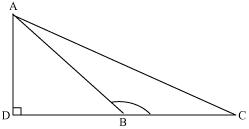
In ∆ADB applying Pythagoras theorem
AB² = AD² + DB² (1)
In ∆ACD applying Pythagoras theorem
AC² = AD² + DC²
AC² = AD² + (DB + BC)²
AC² = AD² + DB² + BC² + 2DB x BC
Now using equation (1)
AC² = AB² + BC² + 2BC . BD

Question 4. In the given figure, ABC is a triangle in which ∆ ABC < 90° and AD ⊥ BC. Prove that AC² = AB² + BC² – 2BC.BD.

Solution:
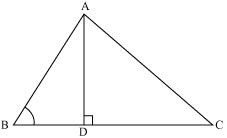
In ∆ADB applying Pythagoras theorem
AD² + DB² = AB²
AD² = AB² – DB² (1)
In ∆ ADC applying Pythagoras theorem
AD² + DC² = AC² (2)
Now using equation (1)
AB² – BD² + DC² = AC²
AB² – BD² + (BC – BD)² = AC²
AC² = AB² – BD² + BC² + BD² – 2BC. BD
= AB² + BC² – 2BC. BD

Question 5. In the given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:

Solution:
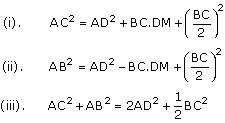
(i). In ∆AMD
AM² + MD² = AD²(1)
In ∆AMC
AM² + MC² = AC² (2)
AM² + (MD + DC)² = AC²
(AM² + MD²) + DC² + 2MD.DC = AC²
Using equation (1) we may get
AD² + DC² + 2MD.DC = AC²

NCERT Solutions for Class 10 Maths Chapter 6 Triangles 118

(ii). In ∆ABM applying Pythagoras theorem
AB² = AM² + MB²
= (AD² – DM²) + MB²
= (AD² – DM²) + (BD – MD)²
= AD² – DM² + BD² + MD^{2 –}2BD.MD
= AD² + BD^{2 –}2BD.MD

NCERT Solutions for Class 10 Maths Chapter 6 Triangles 119

(iii). In ∆AMB
AM² + MB² = AB² (1)
In ∆ AMC
AM² + MC² = AC² (2)
Adding equation (1) and (2)
2AM² + MB² + MC² = AB² + AC²
2AM² + (BD – DM)² + (MD + DC)² = AB² + AC²
2AM²+BD² + DM² – 2BD.DM + MD² + DC² + 2MD.DC = AB² + AC²
2AM² + 2MD² + BD² + DC² + 2MD (-BD + DC) = AB² + AC²

Question 6. Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.

Solution:

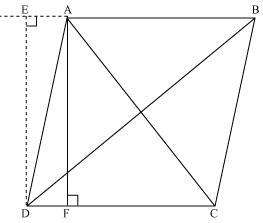
Let ABCD be a parallelogram
Let us draw perpendicular DE on extended side AB and AF on side DC.
In ∆DEA
DE² + EA² = DA² (i)
In ∆DEB
DE² + EB² = DB²
DE² + (EA + AB)² = DB²
(DE² + EA²) + AB² + 2EA. AB = DB²
DA² + AB² + 2EA.AB = DB² (ii)
In ∆ADF
AD² = AF² + FD²
In ∆ AFC
AC² = AF² + FC²
= AF² + (DC – FD)²
= AF² + DC² + FD² – 2DC – FD
= (AF² + FD²) + DC² – 2DC . FD
AC² = AD² + DC² – 2DC FD (iii)
Since ABCD is a parallelogram
AB = CD (iii)
And BC = AD (iv)
In ∆DEA and ∆ADF
∠ DEA = ∠ AFD
∠ EAD = ∠ FDA (EA || DF)
∠ EDA = ∠ FAD (AF || ED)
AD is common in both triangles.
Since respective angles are same and respective sides are same
∆DEA ≅ ∆AFD
So EA = DF (v)
Adding equation (ii) and (iii)
DA² + AB² + 2EA.AB + AD² + DC² – 2DC.FD = DB² + AC²
DA² + AB² + AD²+ DC² + 2EA.AB – 2DC.FD = DB² + AC²
BC² + AB² + AD² + DC² + 2EA.AB-2AB.EA = DB² + AC²
AB² + BC² + CD² + DA² = AC² + BD²

Question 7. In the given figure, two chords AB and CD intersect each other at the point P.
prove that: (i) ∆APC ~ ∆DPB (ii) AP.PB = CP.DP

Solution:

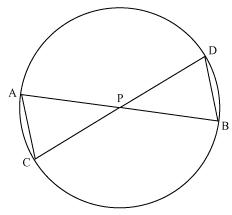
Let us join CB
(i)   In ∆APC and ∆DPB
∠APC = ∠DPB   {Vertically opposite angles}
∠CAP = ∠BDP   {Angles in same segment for chord CB}
∆APC ~ ∆DPB   {BY AA similarly criterion}
(ii)   We know that corresponding sides of similar triangles are proportional

NCERT Solutions for Class 10 Maths Chapter 6 Triangles 124

Question 8. In the given figure, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that

(i) ∆PAC ~ ∆PDB   (ii) PA.PB = PC.PD

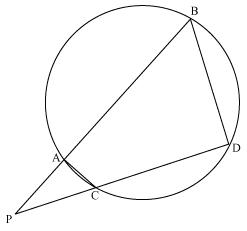
Solution:
(i)   In ∆PAC and ∆PDB
∠ P = ∠ P       (common)
∠ PAC = ∠ PDB   (exterior angle of a cyclic quadrilateral is equal to opposite interior angle)
∠ PCA = ∠PBD
∆PAC ~ ∆PDB

(ii) We know that corresponding sides of similar triangles are proportional.

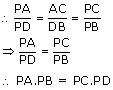
Question 9. In the given figure, D is a point on side BC of ∆ ABC such that $\frac { BD }{ CD } =\frac { AB }{ AC }$ Prove that AD is the bisector of ∠ BAC.

Solution:
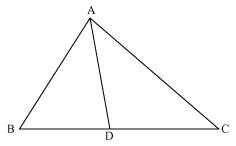
In ∆ DBA and ∆DCA
$\frac { BD }{ CD } =\frac { AB }{ AC }$

(given)
AD = AD (common)
So, ∆DBA ~ ∆DCA (By SSS)
Now, corresponding angles of similar triangles will be equal.
∠ BAD = ∠ CAD
AD is angle bisector of ∠ BAC.

Question 10. Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out (see Fig. If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?

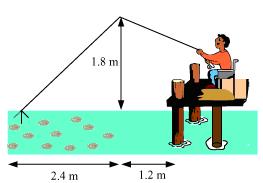
Solution:

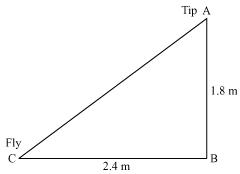
Let AB be the height of tip of fishing rod from water surface. Let BC be the horizontal distance of fly from the tip of fishing rod.
Then, AC is the length of string.
AC can be found by applying Pythagoras theorem in ∆ABC
AC² = AB² + BC²
AC² = (1.8)² + (2.4)²
AC² = 3.24 + 5.76
AC² = 9.00
AC = √9 = 3
Thus, length of string out is 3 m.
Now, she pulls string at rate of 5 cm per second.
So, string pulled in 12 seconds = 12 x 5 = 60 cm = 0.6 m

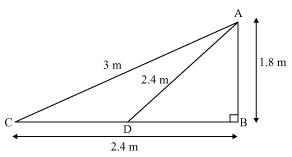
Let after 12 second Fly be at point D.
Length of string out after 12 second is AD
AD = AC – string pulled by Nazima in 12 seconds
= 3.00 – 0.6
= 2.4
In ∆ ADB
AB² + BD² = AD²
(1.8)² + BD² = (2.4)²
BD² = 5.76 – 3.24 = 2.52
BD = 1.587
Horizontal distance of fly = BD + 1.2
= 1.587 + 1.2
= 2.787
= 2.79 m.

We hope the NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.6 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.6, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.6

Reader Interactions

Leave a Reply Cancel reply

Footer