NCERT Solutions for Class 10 Maths Chapter 4 Quadratic Equations Ex 4.3 are part of NCERT Solutions for Class 10 Maths. Here are we have given Chapter 4 Quadratic Equations Class 10 NCERT Solutions Ex 4.3.
- Quadratic Equations Class 10 Ex 4.1
- Quadratic Equations Class 10 Ex 4.2
- Quadratic Equations Class 10 Ex 4.4
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 4 |
| Chapter Name | Quadratic Equations |
| Exercise | Ex 4.3 |
| Number of Questions Solved | 11 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 4 Quadratic Equations Ex 4.3
Page No: 87
Question 1. Find the roots of the following quadratic equations, if they exist, by the method of completing the square:
(i) 2x2 – 7x +3 = 0
(ii) 2x2 + x – 4 = 0
(iii) 4x2 + 4√3x + 3 = 0
(iv) 2x2 + x + 4 = 0
Solution :


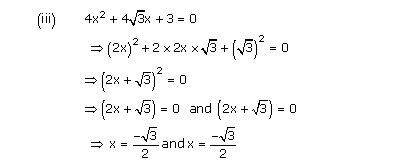
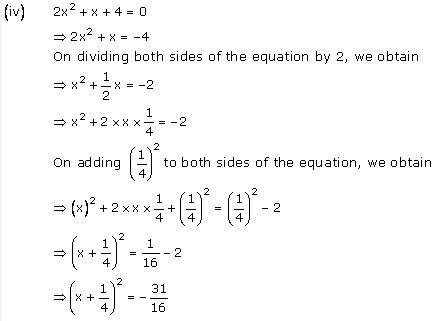
However, the square of a number cannotbe negative.
Therefore, there is no real root for the given equation.
Concept Insight: Before completing the square of any quadratric equation make sure to make the coefficient of square term x2 or y2 unity by dividing the whole equation appropriate real number. Once this is done add and subtract the square of half the coefficient of x or y.
Question 2. Find the roots of the quadratic equations by applying the quadratic formula.
(i) 2x2 – 7x +3 = 0
(ii) 2x2 + x – 4 = 0
(iii) 4x2 + 4√3x + 3 = 0
(iv) 2x2 + x + 4 = 0
Solution :
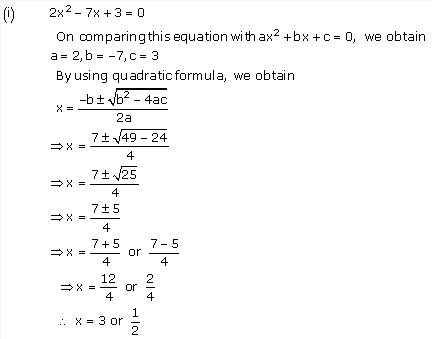

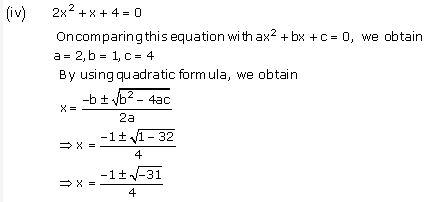
However, the square of a number cannotbe negative.
Therefore, there is no realroot lbr thegivenequation.
Concept Insights: While applying the quadratic formula be careful in applying the rules of radicals for example
\(\sqrt { { a }^{ 2 }+{ b }^{ 2 } } \neq \quad a+b \)
\(\sqrt { -k } \quad \neq \quad -\sqrt { \sqrt { k } } \)
Page No: 88
Question 3. Find the roots of the following equations:
(i) x-1/x = 3, x ≠ 0
(ii) 1/x+4 – 1/x-7 = 11/30, x = -4, 7
Solution :
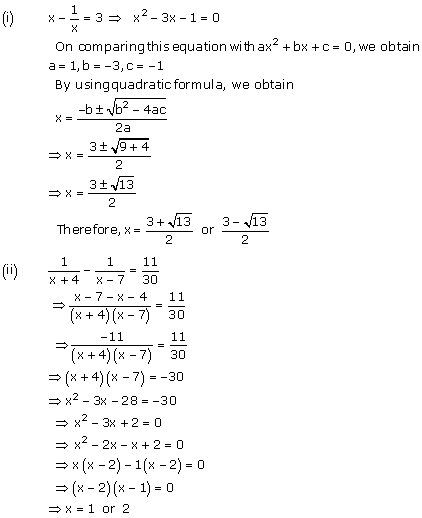
Concept Insights: Apply the arithmetical simplifications appropriately to reduce the equation to quadratic form.
Question 4. The sum of the reciprocals of Rehman’s ages, (in years) 3 years ago and 5 years from now is 1/3. Find his present age.
Solution :
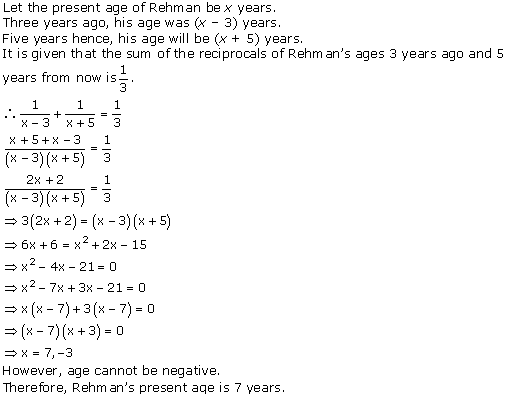
Question 5. In a class test, the sum of Shefali’s marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of their marks would have been 210. Find her marks in the two subjects.
Solution :

Question 6. The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
Solution :
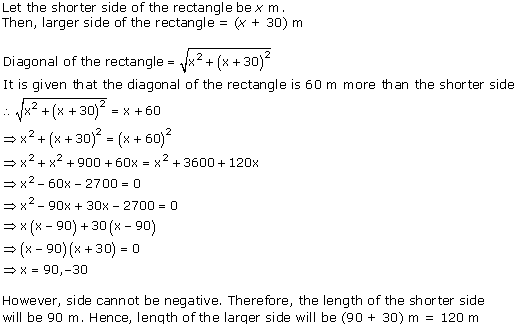
Question 7. The difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers.
Solution :

Question 8. A train travels 360 km at a uniform speed. If the speed had been 5 km/h more, it would have taken 1 hour less for the same journey. Find the speed of the train.
Solution :
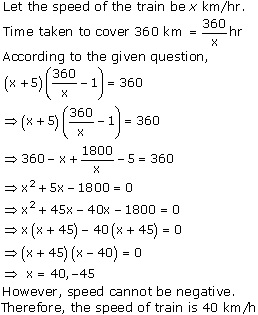
Concept Insight: Use the relation s =d/t to crack this question and remember here distance is constant so speed and time will vary inversely.
Question 9. Two water taps together can fill a tank in hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Solution :
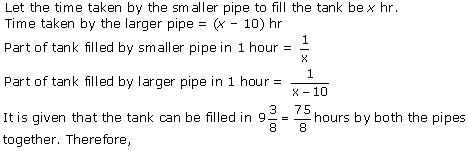

Question 10. An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speeds of the express train is 11 km/h more than that of the passenger train, find the average speed of the two trains.
Solution :
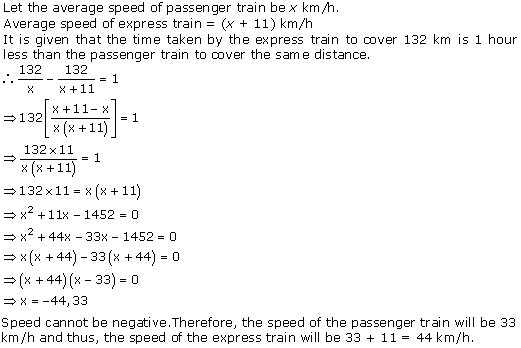
Question 11. Sum of the areas of two squares is 468 m2. If the difference of their perimeters is 24 m, find the sides of the two squares.
Solution :
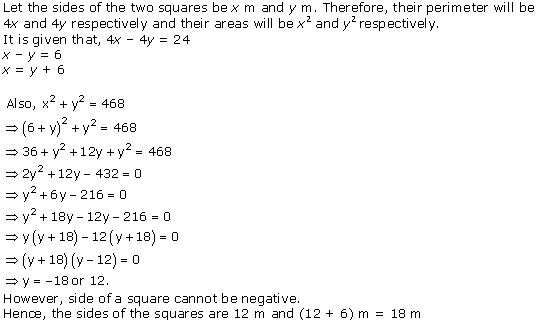
We hope the NCERT Solutions for Class 10 Maths Chapter 4 Quadratic Equations Ex 4.3 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 4 Quadratic Equations Ex 4.3, drop a comment below and we will get back to you at the earliest.
