NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.2 are part of NCERT Solutions for Class 10 Maths. Here are we have given Chapter 2 Polynomials Class 10 NCERT Solutions Ex 2.2.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 2 |
| Chapter Name | Polynomials |
| Exercise | Ex 2.2 |
| Number of Questions Solved | 2 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.2
Page No: 33
Question 1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(i) x2 – 2x – 8
(ii) 4s2 – 4s + 1
(iii) 6x2 – 3 – 7x
(iv) 4u2 + 8u
(v) t2 – 15
(vi) 3x2 – x – 4
Solution:
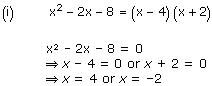
So, the zeroes of x² – 2x – 8 are 4 and -2.
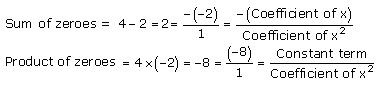
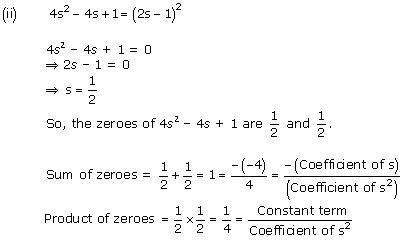
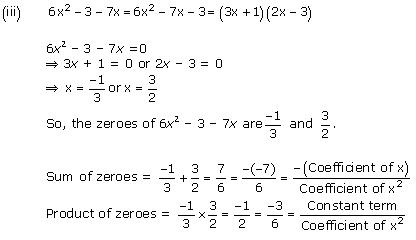
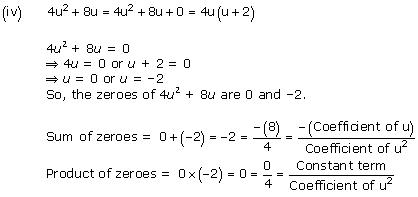
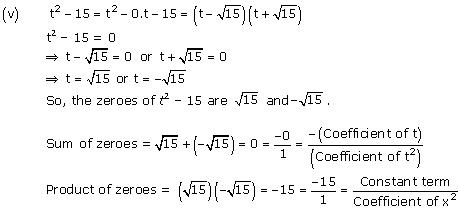
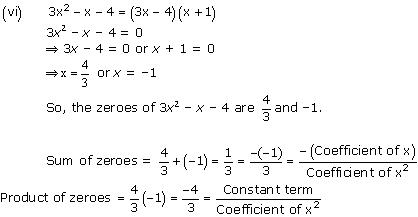
Concept Insight: The zero of a polynomial is that value of the variable which when substituted in the polynomial makes its value 0. When a quadratic polynomial is equated to 0, then the values of the variable obtained are the zeroes of that polynomial. The relationship between the zeroes of a quadratic polynomial with its coefficients is very important. Also, while verifying the above relationships, be careful about the signs of the coefficients.
Question 2. Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
(i) 1/4, -1
(ii) √2, 1/3
(iii) 0, √5
(iv) 1,1
(v) -1/4,1/4
(vi) 4,1
Solution:
(i) Let the required polynomial be ax² + bx + c, and let its zeroes α and β
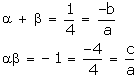
If a = 4k, then b = -k, c = -4k Therefore, the quadratic polynomial is k(4 x 2 – x – 4), where k is a real number .
(ii) Let the polynomial be ax² + bx + c, and let its zeroes be α and β

(iii) Let the polynomial be ax² + bx + c, and let its zeroes be α and β
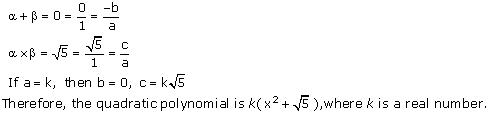
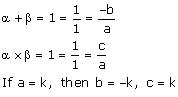
(iv) Let the polynomial be ax² + bx + c, and let its zeroes be α and β
Therefore, the quadratic polynomial is k(x² – x + 1), where k is a real number.
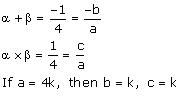
(v) Let the polynomial be ax² + bx + c, and its zeroes be α and β
Therefore, the quadratic polynomial is k(4x² + x + 1),where k is a real number .
(vi) Let the polynomial be ax² + bx + c.
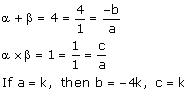
Therefore, the quadratic polynomial is k(x² – 4x + 1), where k is a real number.
Concept Insight: Since the sum and product of zeroes give 2 relations between three unknowns so we assign a value to the variable a and obtain other values.
Alternatively, If the sum and the product of the zeroes of a quadratic polynomial is given then polynomial is given by, where k is a constant. And the simplest polynomial will be the one in which k = 1.
We hope the NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.2 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.2, drop a comment below and we will get back to you at the earliest.
