NCERT Solutions for Class 10 Maths Chapter 14 Statistics Ex 14.3 are part of NCERT Solutions for Class 10 Maths. Here are we have given Chapter 14 Statistics Class 10 NCERT Solutions Ex 14.3.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 14 |
| Chapter Name | Statistics |
| Exercise | Ex 14.3 |
| Number of Questions Solved | 7 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 14 Statistics Ex 14.3
NCERT Solutions for Class 10 Maths
Question 1.
The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality. Find the median, mean and mode of the data and compare them.
| Monthly consumption (in units) | Number of consumers |
| 65 – 85 | 4 |
| 85 – 105 | 5 |
| 105 – 125 | 13 |
| 125 – 145 | 20 |
| 145 – 165 | 14 |
| 165 – 185 | 8 |
| 185 – 205 | 4 |
Solution:
We may find class marks by using the relation
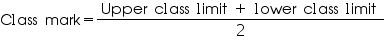
Taking 135 as assumed mean (a) we may find di, ui, fiui, according to step deviation method as following
| Monthly consumption (in units) | Number of consumers (f i) | xi class mark | di = xi – 135 |  | fiui |
| 65 – 85 | 4 | 75 | – 60 | – 3 | – 12 |
| 85 – 105 | 5 | 95 | – 40 | – 2 | – 10 |
| 105 – 125 | 13 | 115 | – 20 | – 1 | – 13 |
| 125 – 145 | 20 | 135 | 0 | 0 | 0 |
| 145 – 165 | 14 | 155 | 20 | 1 | 14 |
| 165 – 185 | 8 | 175 | 40 | 2 | 16 |
| 185 – 205 | 4 | 195 | 60 | 3 | 12 |
| Total | 68 | 7 |
From the table we may observe that
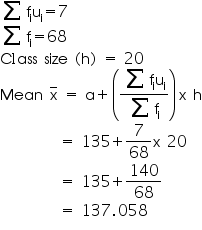
Now from table it is clear that maximum class frequency is 20 belonging to class interval 125 – 145.
Modal class = 125 – 145
Lower limit (l) of modal class = 125
Class size (h) = 20
Frequency (f1) of modal class = 20
Frequency (f0) of class preceding modal class = 13
Frequency (f2) of class succeeding the modal class = 14
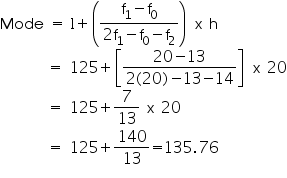
We know that
3 median = mode + 2 mean
= 135.76 + 2 (137.058)
= 135.76 + 274.116
= 409.876
Median = 136.625
So median, mode, mean of given data is 136.625, 135.76, 137.05 respectively.
Question 2.
If the median of the distribution is given below is 28.5, find the values of x and y.
| Class interval | Frequency |
| 0 – 10 | 5 |
| 10 – 20 | x |
| 20 – 30 | 20 |
| 30 – 40 | 15 |
| 40 – 50 | y |
| 50 – 60 | 5 |
| Total | 60 |
Solution:
We may find cumulative frequency for the given data as following
| Class interval | Frequency | Cumulative frequency |
| 0 – 10 | 5 | 5 |
| 10 – 20 | x | 5 + x |
| 20 – 30 | 20 | 25 + x |
| 30 – 40 | 15 | 40 + x |
| 40 – 5 | y | 40 + x + y |
| 50 – 60 | 5 | 45 + x + y |
| Total (n) | 60 |
It is clear that n = 60
45 + x + y = 60
x + y = 15 (1)
Median of data is given as 28.5 which lies in interval 20 – 30.
So, median class = 20 – 30
Lower limit (l) of median class = 20
Cumulative frequency (cf) of class preceding the median class = 5 + x
Frequency (f) of median class = 20
Class size (h) = 10
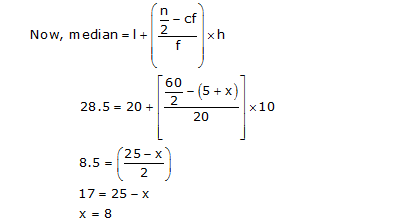
From equation (1)
8 + y = 15
y = 7
Hence values of x and y are 8 and 7 respectively.
Question 3
A life insurance agent found the following data for distribution of ages of 100 policy holders. Calculate the median age, if policies are given only to persons having age 18 years onwards but less than 60 year.
| Age (in years) | Number of policy holders |
| Below 20 | 2 |
| Below 25 | 6 |
| Below 30 | 24 |
| Below 35 | 45 |
| Below 40 | 78 |
| Below 45 | 89 |
| Below 50 | 92 |
| Below 55 | 98 |
| Below 60 | 100 |
Solution:
Here class width is not same. There is no need to adjust the frequencies according to class intervals. Now given frequency table is of less than type represented with upper class limits. As policies were given only to persons having age 18 years onwards but less than 60 years, we can define class intervals with their respective cumulative frequency as below
| Age (in years) | Number of policy holders (fi) | Cumulative frequency (cf) |
| 18 – 20 | 2 | 2 |
| 20 – 25 | 6 – 2 = 4 | 6 |
| 25 – 30 | 24 – 6 = 18 | 24 |
| 30 – 35 | 45 – 24 = 21 | 45 |
| 35 – 40 | 78 – 45 = 33 | 78 |
| 40 – 45 | 89 – 78 = 11 | 89 |
| 45 – 50 | 92 – 89 = 3 | 92 |
| 50 – 55 | 98 – 92 = 6 | 98 |
| 55 – 60 | 100 – 98 = 2 | 100 |
| Total (n) |
Now from table we may observe that n = 100.
Cumulative frequency (cf) just greater than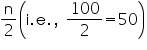 
is 78 belonging to interval 35 – 40
So, median class = 35 – 40
Lower limit (l) of median class = 35
Class size (h) = 5
Frequency (f) of median class = 33
Cumulative frequency (cf) of class preceding median class = 45
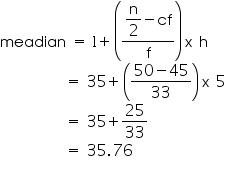
So, median age is 35.76 years.
Question 4.
The lengths of 40 leaves of a plant are measured correct to the nearest millimeter, and the data obtained is represented in the following table:
| Length (in mm) | Number or leaves fi |
| 118 – 126 | 3 |
| 127 – 135 | 5 |
| 136 – 144 | 9 |
| 145 – 153 | 12 |
| 154 – 162 | 5 |
| 163 – 171 | 4 |
| 172 – 180 | 2 |
Find the median length of the leaves.
(Hint: The data needs to be converted to continuous classes for finding the median, since the formula assumes continuous classes. The classes then change to 117.5 – 126.5, 126.5 – 135.5 – 171.5 – 180.5)
Solution:
The given data is not having continuous class intervals. We can observe that difference between two class intervals is 1. So, we have to add and subtract 1/2=0.5 to upper class limits and lower class limits.
Now continuous class intervals with respective cumulative frequencies can be represented as below
| Length (in mm) | Number or leaves fi | Cumulative frequency |
| 117.5 – 126.5 | 3 | 3 |
| 126.5 – 135.5 | 5 | 3 + 5 = 8 |
| 135.5 – 144.5 | 9 | 8 + 9 = 17 |
| 144.5 – 153.5 | 12 | 17 + 12 = 29 |
| 153.5 – 162.5 | 5 | 29 + 5 = 34 |
| 162.5 – 171.5 | 4 | 34 + 4 = 38 |
| 171.5 – 180.5 | 2 | 38 + 2 = 40 |
From the table we may observe that cumulative frequency just greater then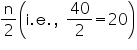 
is 29, belonging to class interval 144.5 – 153.5.
Median class = 144.5 – 153.5
Lower limit (l) of median class = 144.5
Class size (h) = 9
Frequency (f) of median class = 12
Cumulative frequency (cf) of class preceding median class = 17
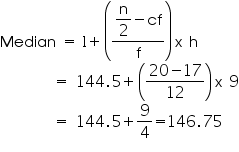
So, median length of leaves is 146.75 mm.
Question 5.
Find the following tables gives the distribution of the life time of 400 neon lamps:
| Life time (in hours) | Number of lamps |
| 1500 – 2000 | 14 |
| 2000 – 2500 | 56 |
| 2500 – 3000 | 60 |
| 3000 – 3500 | 86 |
| 3500 – 4000 | 74 |
| 4000 – 4500 | 62 |
| 4500 – 5000 | 48 |
Find the median life time of a lamp.
Solution:
We can find cumulative frequencies with their respective class intervals as below –
| Life time | Number of lamps (fi) | Cumulative frequency |
| 1500 – 2000 | 14 | 14 |
| 2000 – 2500 | 56 | 14 + 56 = 70 |
| 2500 – 3000 | 60 | 70 + 60 = 130 |
| 3000 – 3500 | 86 | 130 + 86 = 216 |
| 3500 – 4000 | 74 | 216 + 74 = 290 |
| 4000 – 4500 | 62 | 290 + 62 = 352 |
| 4500 – 5000 | 48 | 352 + 48 = 400 |
| Total (n) | 400 |
Now we may observe that cumulative frequency just greater than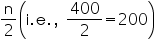 
is 216 belonging to class interval 3000 – 3500.
Median class = 3000 – 3500
Lower limit (l) of median class = 3000
Frequency (f) of median class = 86
Cumulative frequency (cf) of class preceding median class = 130
Class size (h) = 500
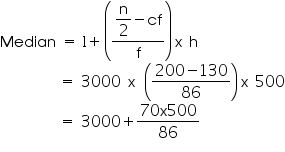
So, median life time of lamps is 3406.98 hours.
Question 6.
100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:
| Number of letters | 1 – 4 | 4 – 7 | 7 – 10 | 10 – 13 | 13 – 16 | 16 – 19 |
| Number of surnames | 6 | 30 | 40 | 6 | 4 | 4 |
Determine the median number of letters in the surnames. Find the mean number of letters in the surnames? Also, find the modal size of the surnames.
Solution:
We can find cumulative frequencies with their respective class intervals as below
| Number of letters | Frequency (fi) | Cumulative frequency |
| 1 – 4 | 6 | 6 |
| 4 – 7 | 30 | 30 + 6 = 36 |
| 7 – 10 | 40 | 36 + 40 = 76 |
| 10 – 13 | 16 | 76 + 16 = 92 |
| 13 – 16 | 4 | 92 + 4 = 96 |
| 16 – 19 | 4 | 96 + 4 = 100 |
| Total (n) | 100 |
Now we may observe that cumulative frequency just greater than is 76 belonging to class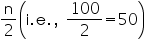 
interval 7 – 10.
Median class = 7 – 10
Lower limit (l) of median class = 7
Cumulative frequency (cf) of class preceding median class = 36
Frequency (f) of median class = 40
Class size (h) = 3
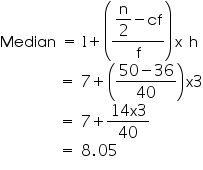
Now we can find class marks of given class intervals by using relation
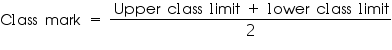
Taking 11.5 as assumed mean (a) we can find di, ui and fiui according to step deviation method as below.
| Number of letters | Number of surnames | xi | xi – a |  | fiui |
| 1 – 4 | 6 | 2.5 | -9 | -3 | -18 |
| 4 – 7 | 30 | 5.5 | -6 | -2 | -60 |
| 7 – 10 | 40 | 8.5 | -3 | -1 | -40 |
| 10 – 13 | 16 | 11.5 | 0 | 0 | 0 |
| 13 – 16 | 4 | 14.5 | 3 | 1 | 4 |
| 16 – 19 | 4 | 17.5 | 6 | 2 | 8 |
| Total | 100 | -106 |
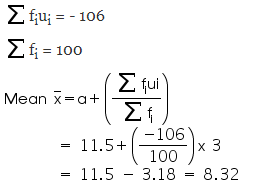
We know that
3 median = mode + 2 mean
3(8.05) = mode + 2(8.32)
24.15 – 16.64 = mode
7.51 = mode
So, median number and mean number of letters in surnames is 8.05 and 8.32 respectively while modal size of surnames is 7.51.
Question 7
The distribution below gives the weights of 30 students of a class. Find the median weight of the students.
| Weight (in kg) | 40 – 45 | 45 – 50 | 50 – 55 | 55 – 60 | 60 – 65 | 65 – 70 | 70 – 75 |
| Number of students | 2 | 3 | 8 | 6 | 6 | 3 | 2 |
Solution:
We may find cumulative frequencies with their respective class intervals as below
Cumulative frequency just greater than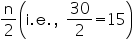 
is 19, belonging to class interval 55 – 60.
Median class = 55 – 60
Lower limit (l) of median class = 55
Frequency (f) of median class = 6
Cumulative frequency (cf) of median class = 13
Class size (h) = 5
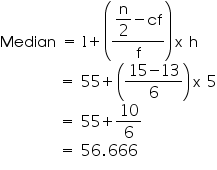
So, median weight is 56.67 kg.
We hope the NCERT Solutions for Class 10 Maths Chapter 14 Statistics Ex 14.3 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 14 Statistics Ex 14.3, drop a comment below and we will get back to you at the earliest.