NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.3 are part of NCERT Solutions for Class 10 Maths. Here are we have given Chapter 1 Real Numbers Class 10 NCERT Solutions Ex 1.3.
- Real Numbers Class 10 Ex 1.1
- Real Numbers Class 10 Ex 1.2
- Real Numbers Class 10 Ex 1.3
- Real Numbers Class 10 Ex 1.4
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 1 |
| Chapter Name | Real Numbers |
| Exercise | Ex 1.3 |
| Number of Questions Solved | 3 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.3
Page No: 14
Question 1
Prove that √5 is irrational.
Solution:
Let us assume, on the contrary, that √5 is a rational number.
Therefore, we can find two integers a,b (b # 0) such that √5 = a\b
Where a and b are co-prime integers.
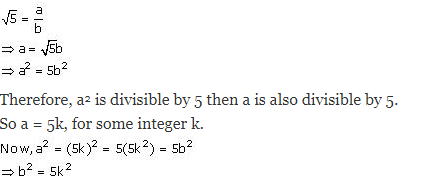
This means that b2 is divisible by 5 and hence, b is divisible by 5.
This implies that a and b have 5 as a common factor.
And this is a contradiction to the fact that a and b are co-prime.
So our assumption that √5 is rational wrong.
Hence,√5 cannot be a rational number. Therefore, √5 is rational.
You can also Download Class 10 Maths NCERT Solutions to help you to revise complete Syllabus and score more marks in your examinations.
Concept Insight: There are various ways of proving in mathematics proof by contradiction is one of them. In this approach, we assume something which is contrary to what needs to be proved and arrive at a fact which contradicts something which is true in general. Key result used here is “If P is a prime number and it divides a2then it divides a as well”.
Question 2
Prove that 3 + 2√5 is irrational.
Solution:
Let us assume, on the contrary that 3 + 2√5 is rational,
Therefore, we can find two integers a, b (b ≠ 0) such that

Concept Insight: This problem is solved using proof by contradiction. The key concept used is if p is a prime number then √P is irrational. Do not prove this question by assuming sum of rational and irrational is irrational.
Question 3
Prove that the following are irrationals:
(i) 1/√2
(ii) 7√5
(iii) 6 + √2
Solution:



Concept Insight: This problem is solved using proof by contradiction. The key concept used is if p is a prime number then √P is irrational. Do not prove this question by assuming sum or product of rational and irrational is irrational.
We hope the NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.3 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.3, drop a comment below and we will get back to you at the earliest.
