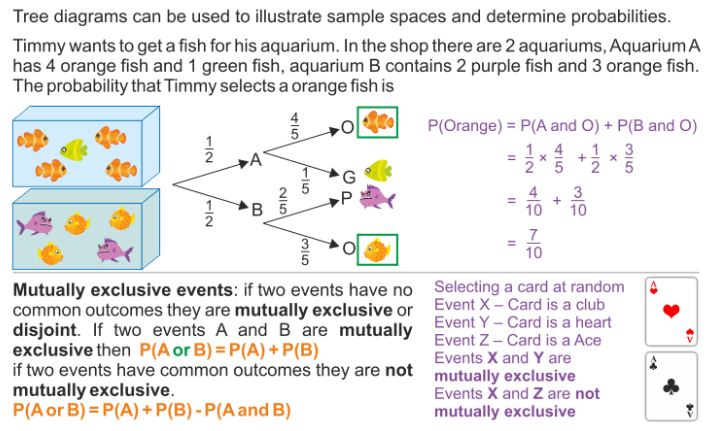
Mutually Exclusive Events
An event is a set of outcomes. It is a subset of the sample space for an activity or experiment.
Event: Drawing a black card from a deck of standard cards.
Probability of this event = 26/52 = 1/2
When an event corresponds to a single outcome of the activity, it is often called a simple event.
Simple Event: Drawing the queen of spades from a deck of standard cards.
Probability of this event = 1/52
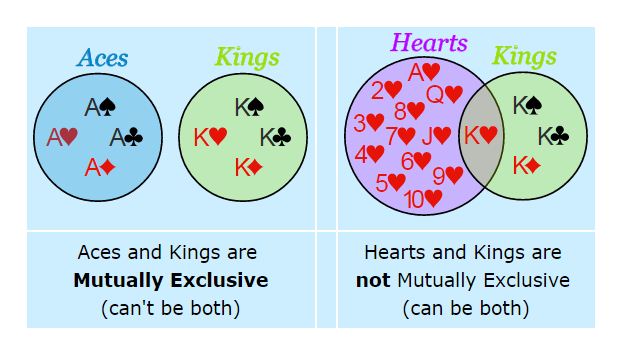
Two events that have NO outcomes in common are called mutually exclusive.
These are events that cannot occur at the same time.
Mutually exclusive – think of this as the 2 events together (mutually) agreeing to exclude (not include) each others’ elements.
They have agreed to be different – mutually exclusive.
Examples:
- A pair of dice is rolled. The events of rolling a 6 and of rolling a double have the outcome (3,3) in common. These two events are NOT mutually exclusive.
- A pair of dice is rolled. The events of rolling a 9 and of rolling a double have NO outcomes in common. These two events ARE mutually exclusive.
For any two mutually exclusive events, the probability that an outcome will be in one event or the other event is the sum of their individual probabilities.
If A and B are mutually exclusive events,
P(A or B) = P(A) + P(B)
For any two events which are not mutually exclusive, the probability that an outcome will be in one event or the other event is the sum of their individual probabilities minus the probability of the outcome being in both events.
If events A and B are NOT mutually exclusive,
P(A or B) = P(A) + P(B) – P(A and B)
Example 1: A pair of dice is rolled. What is the probability that the sum of the numbers rolled is either 7 or 11?
Answer: Six outcomes have a sum of 7:
(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)
P(7) = 6/36
Two outcomes have a sum of 11:
(5,6), (6,5)
P(11) = 2/36
The sum of the numbers cannot be 7 and 11 at the same time, so these events are mutually exclusive.
P(7 or 11) = P(7) + P(11) = 6/36 + 2/36 = 8/36 = 2/9
Example 2: A pair of dice is rolled. What is the probability that the sum of the numbers rolled is either an even number or a multiple of 3?
Answer: Of the 36 possible outcomes, 18 are even sums.
P(even) = 18/36 = 1/2
Sums of 3, 6, 9, and 12 are multiples of 3.
There are 12 sums that are multiples of 3.
P(multiple of 3)= 12/36 = 1/3
However, some of these outcomes appear in both events.
(not mutually exclusive)
The sums that are even and a multiple of 3 are 6 and 12.
There are 6 ordered pairs with these sums.
P(even AND a multiple of 3) = 6/36 = 1/6
P(even OR a multiple of 3) = 18/36 + 12/36 – 6/36 = 24/36 = 2/3
