Multiplying Powers
Rule: For all numbers x and all integers m and n,
xm • xn = xm+n
“This simply means when you are multiplying, and the bases are the same, you ADD the exponents.”
Consider:
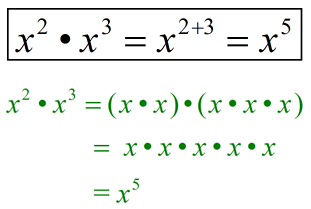
Observe this rule at work in the following examples:
- The bases are the same (all 5’s), so the exponents are added.
52 × 54 = 52+4 = 56 - The bases are the same, so the exponents are added. Notice how the numbers in front of the bases (7 and 1) are being multiplied.
7x3 • x5 = 7x8 - The bases are the same (all a’s), so the exponents are added.
22(23) (25) = 22+3+5 = 210 - The bases are the same (all x’s), so the exponents are added.
Be careful when adding the negative exponent.
5-2 × 56 = 5-2+6 = 54 - The bases are the same, so the exponents are added.
The numbers in front of the bases are multiplied.
2x3 • 3x5 • 2x6 = 12x3+5+6 = 12x14
Take one more look at the distributive property at work with a set of parentheses, along with this new rule:
Use the distributive property to simplify:
3x2 (2x3 + 4) = 3x2 (2x3) + 3x2 (4) = 6x5 + 12x2
The distributive property is applied in this problem. (Multiply each term inside the parentheses by the 3x2 term.)
Then the exponents in the first portion are added since their bases are the same. The numbers in front (the coefficients) are multiplied.
Remember that you cannot add 6x5 and 12x2 since they are not similar (like) terms.
