Multiplying and Dividing Scientific Notation
As you already know, scientific notation (a form of exponential notation) is a concise way to express very small or very large numbers.
Consider the speed of light, 300,000,000 m/sec. When writing this value it is very easy to “lose” one, or more, of the zeros. It is much faster and easier to write 3.0 × 108 m/sec or 3.0 E+8 m/sec.
Remember that correctly written scientific notation has two components:
- a number between 1 and 10, such that
1 ≤ n < 10
multiplied by…. n × 10x - a power of 10.
One of the advantages of scientific notation is its ease of use when performing computations.
Watch the laws of exponents at work!
To multiply
To multiply two numbers expressed in scientific notation, simply multiply the numbers out front and add the exponents.
Generically speaking, this process is expressed as:
(n × 10a) • (m × 10b) = (n • m) × 10a+b
Multiply the numbers out front and add the exponents.
Example 1: (5.1 × 104) • (2.5 × 103) = 12.75 × 107 Oops!!
This new answer is no longer in proper scientific notation.
Proper scientific notation is 1.275 × 108
Example 2: (3.4 × 103) • (5.6 × 105)
(3.4 × 103) • (5.6 × 105) = 19.04 × 108 = 1.904 × 109
Notice that the first multiplication did not give the answer in proper scientific notation.
NOTE: In real life situations, answers obtained from the multiplication (or division) of values expressed in scientific notation may result in answers with “more decimal accuracy” than the original values.
Regarding ACCURACY: If values are stated to the greatest accuracy that they are known, then the result of multiplication (or division) with these values cannot be determined to any better accuracy than to the number of digits in the least accurate number. Regarding accuracy, the answer to Example 1 would be 1.3 × 108.
On this site, we will be finding the mathematical results to the multiplication, or division, of scientific notation, WITHOUT a determination of accuracy.
To divide
To divide two numbers expressed in scientific notation, simply divide the numbers out front and subtract the exponents.
Generically speaking, this process is expressed as:
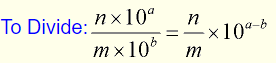
Divide the numbers out front and subtract the exponents.
Example 2:
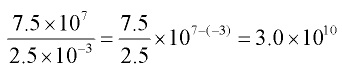
Example 3:
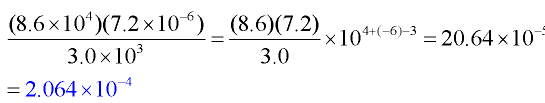
Ever wonder how these numbers are Added or Subtracted?
To add (or subtract) two numbers expressed in scientific notation, be sure that the exponents in each number are the SAME. Generically speaking:
To ADD or SUBTRACT two numbers in scientific notation, the exponents on the power of 10 must be the same. You may need to “adjust” the numbers, moving them out of scientific notation, so the exponents are alike.
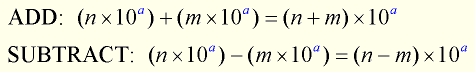
If the exponents are NOT the same, the decimal of one of the numbers has to be repositioned so that its exponent is the same as the other number being added or subtracted. Think of it as lining up the decimals for addition or subtraction.
Example 1: (3.2 × 105) + (5.1 × 104)
(3.2 × 105) + (5.1 × 104) = (3.2 × 105) + (0.51 × 105)
= 3.71 × 105
Example 1: (6.3 × 106) + (4.7 × 104)
(6.3 × 106) + (4.7 × 104) = (6.3 × 106) + (0.047 × 106)
= 6.347 × 106
The decimal point in the second number was moved two places to the left so that the base of 10 could be raised to a power of 6.
