Multiplying and Dividing Algebraic Fractions
Multiplication and division of algebraic fractions is actually an extension of reducing fractions, except that now there are two fractions in the problem instead of just one.
Steps to Multiplying Algebraic Fractions:
- Factor first if possible.
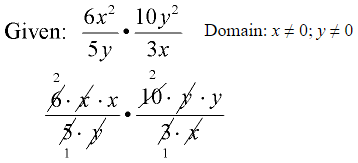
- Then reduce common factors between any numerator and denominator.
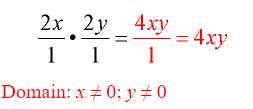
- Reducing may be done up-down, NOT across (horizontally).
Example 1:

- Factor first.
- Reduce common factors.
- Do NOT reduce single terms from within parentheses containing a “+” or “-” sign. Reduce the entire
- parentheses.
- State the domain if so directed by the problem or by your teacher.
Example 2:
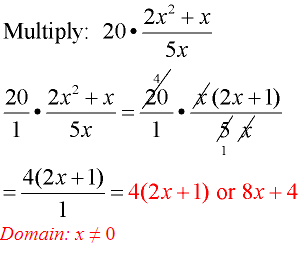
- Multiplying by 20 is the same as multiplying by \(\frac { 20 }{ 1} \). Writing \(\frac { 20 }{ 1 } \) may make the process more observable.
- Factor the numerator of the fraction.
- Reduce common factors.
Example 3:
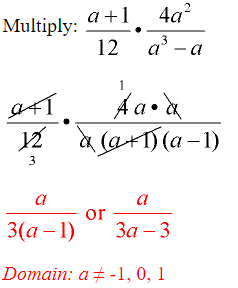
- Factor first.
- The denominator of the second fraction factors:
a³ – a = a(a² – 1) = a(a + 1)(a – 1) - Reduce common factors (top with bottom).
Steps to Dividing Algebraic Fractions:
- Invert (flip) the second fraction, and change the division sign to multiply.
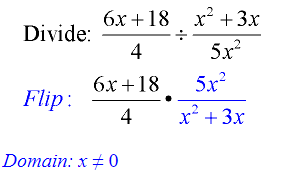
- Factor, if possible.
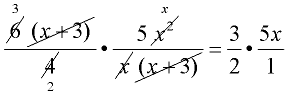
- Mutliply through the numerator and multiply through the denominator.
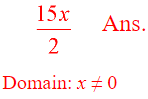
Example 1:

- Flip second fraction and change division sign to multiply.
- Factor.
- Reduce common factors.
This example shows one way to reduce the factors.
Example 2:
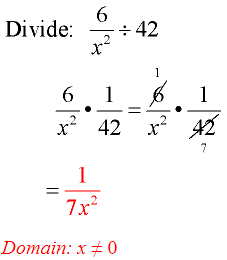
- Remember that 42 is really \(\frac { 42 }{ 1 } \).
- Flip second fraction and change to multiplication.
- Factor and reduce common factors.
Example 3:
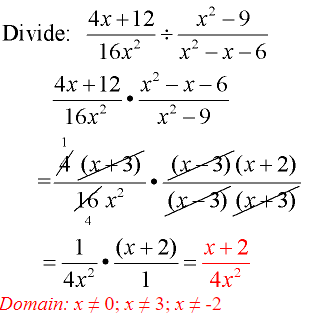
- Flip second fraction and change to multiplication.
- Factor.
- Reduce common factors.
Be careful to reduce entire parentheses.
