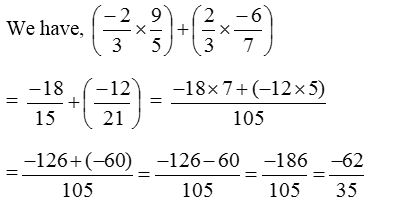A Plus Topper

Improve your Grades

How do you Multiply and Divide Rational Numbers?

by

How do you Multiply and Divide Rational Numbers?

Multiplication of Rational Numbers

(a) Let \(\frac { a }{ b }\) and c are two rational numbers, then \(\frac { a }{ b } \times c=\frac { ac }{ b }\)
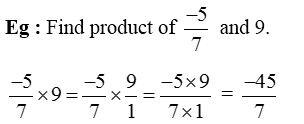
How do you Multiply and Divide Rational Numbers 1
(b) When we multiply two rational numbers :
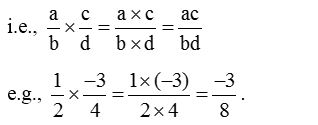
How do you Multiply and Divide Rational Numbers 2

  1. On multiplying two rational numbers, we get result as a rational number.
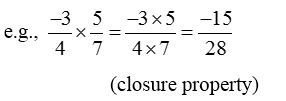
    How do you Multiply and Divide Rational Numbers 3
  2. \(\frac { 1 }{ 3 } \times \frac { 1 }{ 4 } =\frac { 1 }{ 4 } \times \frac { 1 }{ 3 }\) (commutative i.e., on changing the order the result remains same)
  3. \(\frac { 1 }{ 3 } \times \left( \frac { 1 }{ 4 } \times \frac { 1 }{ 5 }  \right) =\left( \frac { 1 }{ 3 } \times \frac { 1 }{ 4 }  \right) \times \frac { 1 }{ 5 }\) (associative)
  4. If 0 is multiplied to any rational number, the result is always zero.
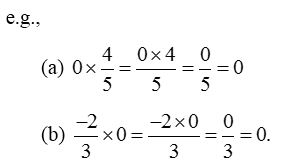
    How do you Multiply and Divide Rational Numbers 4

Multiplication of Rational Numbers on a Number Line

The product of two rational numbers on the number line can be calculated in the following way.
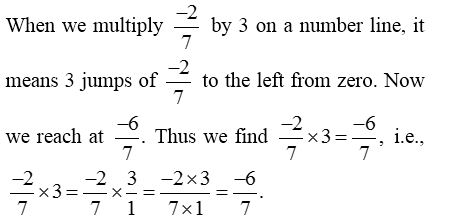
How do you Multiply and Divide Rational Numbers 5
How do you Multiply and Divide Rational Numbers 6
This result reconfirms that the product of two rational numbers is rational number whose numerator is the product of the numerators of the given rational numbers and the denominator is the product of the denominators of the given numbers.
∴  Multiplication is closure (product is rational), commutative (ab = ba) and associative
(a(bc) = (ab)c) for rational number.

Division of Rational Numbers

(a) Let \(\frac { a }{ b }\) be a rational number then its reciprocal will be \(\frac { b }{ a }\)

  1. The product of a rational number with its reciprocal is always 1.
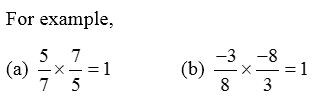
    How do you Multiply and Divide Rational Numbers 7
  2. Zero has no reciprocal as reciprocal of 0 = \(\left( \frac { 0 }{ 1 }  \right)\) is \(\frac { 1 }{ 0 }\) (which is not defined).
  3. The reciprocal of a rational number is called the multiplicative inverse of rational number.
  4. 1 and –1 are the only rational numbers which are their own reciprocal.
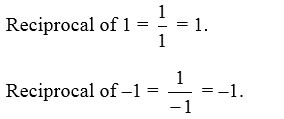
    How do you Multiply and Divide Rational Numbers 8
  5. Reciprocal of a (+ve) rational number is (+ve) and reciprocal of (–ve) rational number is (–ve).
    To divide one rational number by other rational numbers we multiply the rational number by the reciprocal of the other
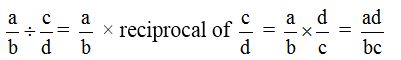
    How do you Multiply and Divide Rational Numbers 9
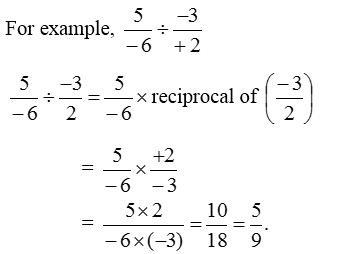
    How do you Multiply and Divide Rational Numbers 10
  6. Zero divided by any rational number is always equal to zero.
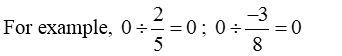
    How do you Multiply and Divide Rational Numbers 11

Note:

  1. When a rational number (except zero) is divided by another rational number (except 0) the quotient is always a rational number. (closed under division)
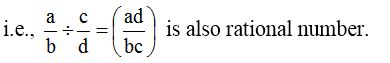
    How do you Multiply and Divide Rational Numbers 12
  2. Division of any rational number by itself gives the quotient 1.
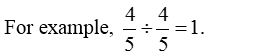
    How do you Multiply and Divide Rational Numbers 13
  3. When a rational number is divided by 1, the quotient is a rational number itself.
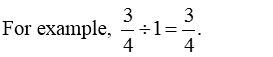
    How do you Multiply and Divide Rational Numbers 14

Multiplication and Division of Rational Numbers Problems with Solutions

1. Find the product:
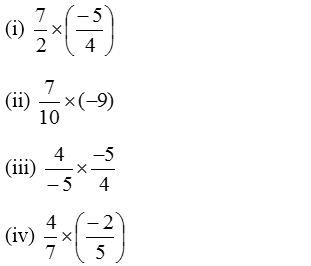
How do you Multiply and Divide Rational Numbers 15
Solution:
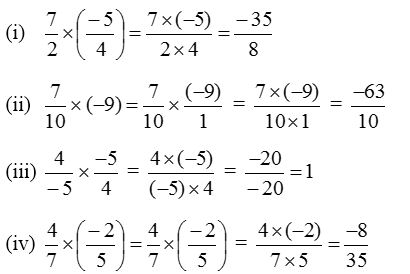
How do you Multiply and Divide Rational Numbers 16
2. Find the value of:
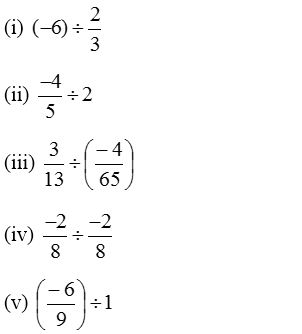
How do you Multiply and Divide Rational Numbers 17
Solution:
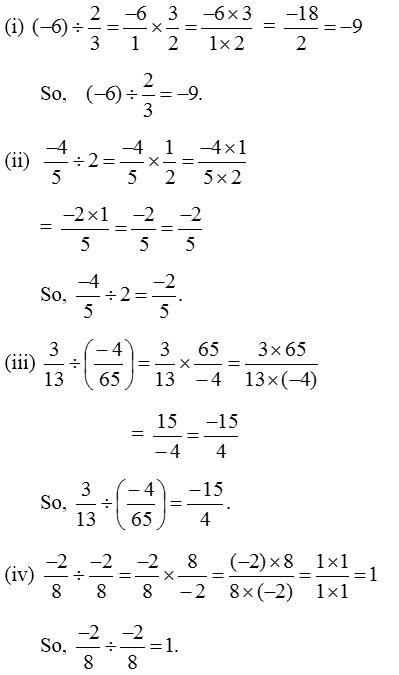
How do you Multiply and Divide Rational Numbers 18
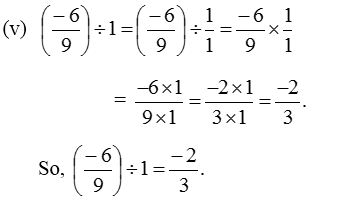
How do you Multiply and Divide Rational Numbers 19
3. Multiply:
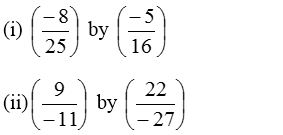
How do you Multiply and Divide Rational Numbers 20
Solution:
How do you Multiply and Divide Rational Numbers 21
4. Simplify:
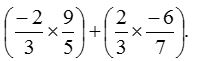
How do you Multiply and Divide Rational Numbers 22
Solution:
How do you Multiply and Divide Rational Numbers 23

Maths