What is the Multinomial Theorem?
Multinomial theorem
Let x1, x2, …….., xm be integers. Then number of solutions to the equation x1 + x2 +…….. + xm = n …..(i)
Subject to the condition
a1 ≤ x1 ≤ b1, a2 ≤ x2 ≤ b2, ……, am ≤ xm ≤ bm …..(ii)
is equal to the coefficient of xn in
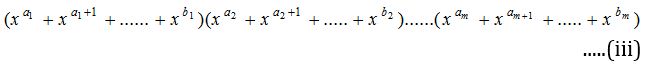
This is because the number of ways, in which sum of m integers in (i) equals n, is the same as the number of times xn comes in (iii).
(1) Use of solution of linear equation and coefficient of a power in expansions to find the number of ways of distribution : (i) The number of integral solutions of x1 + x2 + x3 +…….. + xr = n where x1 ≥ 0, x2 ≥ 0, …….., xr ≥ 0 is the same as the number of ways to distribute n identical things among r persons.
This is also equal to the coefficient of xn in the expansion of (x0 + x1 + x2 + x3 + ……)r
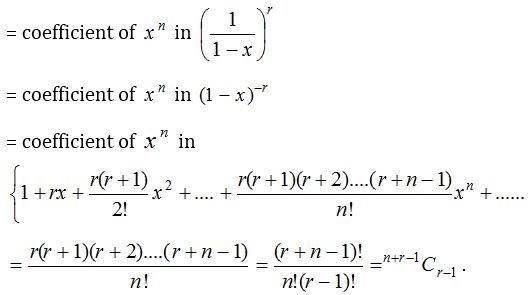
(2) The number of integral solutions of x1 + x2 + x3 +…….. + xr = n where x1 ≥ 1, x2 ≥ 1, …….., xr ≥ 1 is same as the number of ways to distribute n identical things among r persons each getting at least 1. This also equal to the coefficient of xn in the expansion of (x0 + x1 + x2 + x3 + ……)r.
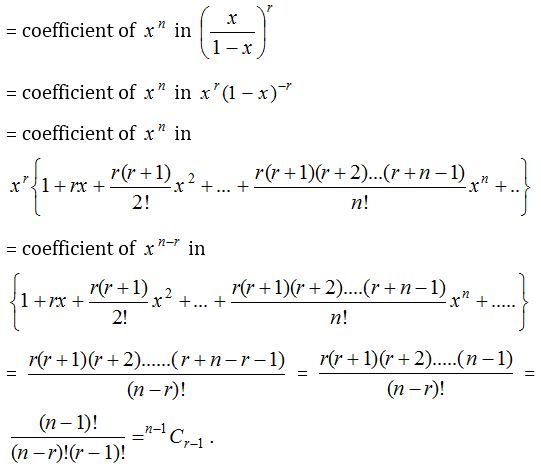
Number of divisors

(5) The number of ways in which N can be resolved as a product of two factors is
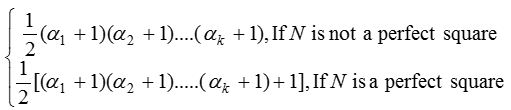
(6) The number of ways in which a composite number N can be resolved into two factors which are relatively prime (or co-prime) to each other is equal to 2n−1 where n is the number of different factors in N.
