Logarithms Class 9 ICSE ML Aggarwal

ML Aggarwal Class 9 Solutions Chapter 9 provides comprehensive guidance and step-by-step explanations for the concepts covered in this chapter Class 9 Mathematics. This chapter typically introduces fundamental mathematical concepts, laying the groundwork for future studies.

ML Aggarwal Class 9 Chapter 9 Solutions

ICSE Class 9 Maths Chapter 9 Solutions ML Aggarwal

Exercise 9.1

Question 1.
Convert the following to logarithmic form:
(i) 5² = 25
(ii) a⁵ =64
(iii) 7^x =100
(iv) 9° = 1
(v) 6¹ = 6
(vi) 3^-2 = \(\frac { 1 }{ 9 }\)
(vii) 10^-2 = 0.01
(viii) (81)^{\(\frac { 3 }{ 4 }\)} = 27
Solution:

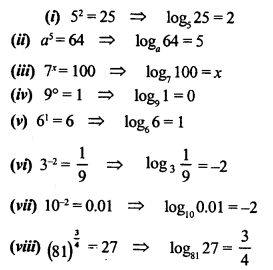
Question 2.
Convert the following into exponential form:
(i) log₂ 32 = 5
(ii) log₃ 81=4
(iii) log₃\(\frac { 1 }{ 3 }\)= -1
(iv) log₃ 4= \(\frac { 2 }{ 3 }\)
(v) log₈ 32= \(\frac { 5 }{ 3 }\)
(vi) log₁₀ (0.001) = -3
(Vii) log₂ 0.25 = -2
(viii) log_a (\(\frac { 1 }{ a }\)) =-1
Solution:

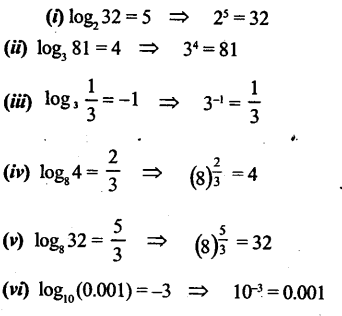
Question 3.
By converting to exponential form, find the values of:
(i) log₂ 16
(ii) log₅ 125
(iii) log₄ 8
(iv) log₉ 27
(v) log₁₀(.01)
(vi) log₇ \(\frac { 1 }{ 7 }\)
(vii) log₅ 256
(Viii) log₂ 0.25
Solution:

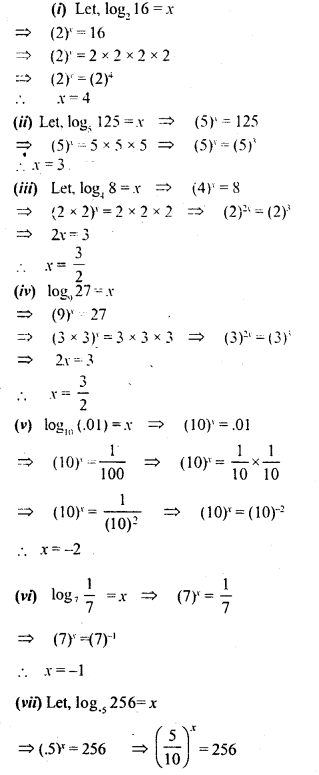
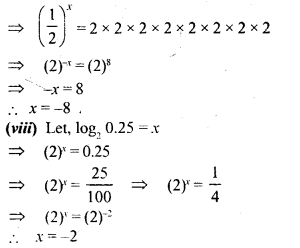
Question 4.
Solve the following equations for x.

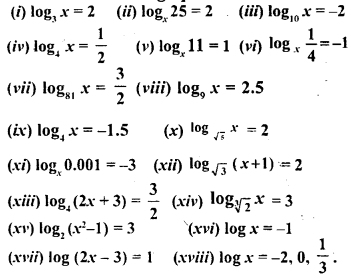
Solution:

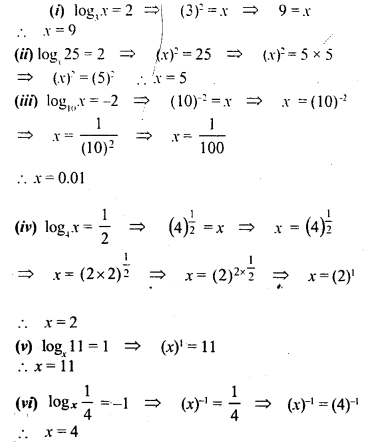
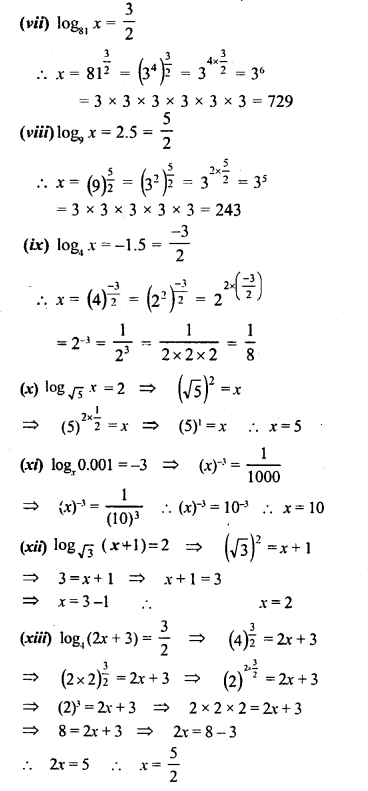
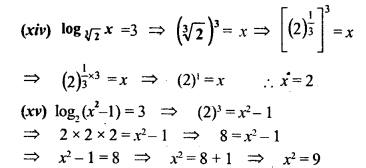
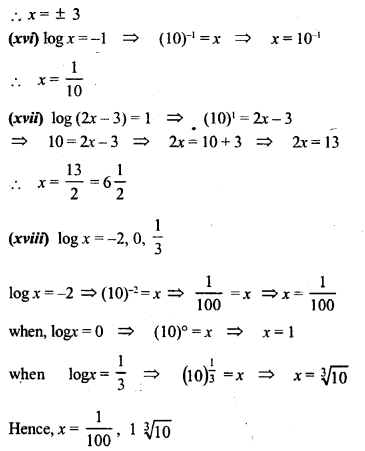
Question 5.
Given log₁₀a = b, express 10^2b-3 in terms of a.
Solution:

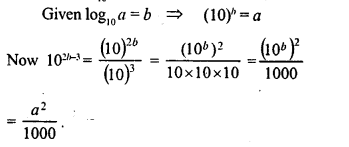
Question 6.
Given log₁₀ x= a, log₁₀ y = b and log₁₀ z =c,
(i) write down 10^2a-3 in terms of x.
(ii) write down 10^3b-1 in terms of y.
(iii) if log₁₀ P = 2a + \(\frac { b }{ 2 }\)– 3c, express P in terms of x, y and z.
Solution:

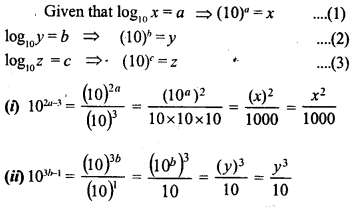
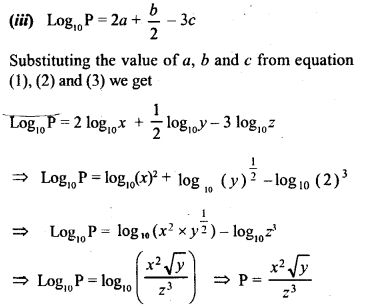
Question 7.
If log₁₀x = a and log₁₀y = b, find the value of xy.
Solution:

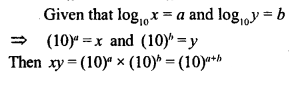
Question 8.
Given log₁₀ a = m and log₁₀ b = n, express \(\frac { { a }^{ 3 } }{ { b }^{ 2 } }\) in terms of m and n.
Solution:

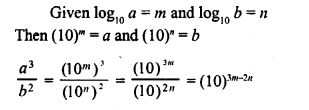
Question 9.
Given log₁₀a= 2a and log₁₀y = –\(\frac { b }{ 2 }\)
(i) write 10^a in terms of x.
(ii) write 10^2b+1 in terms of y.
(iii) if log₁₀P= 3a -2b, express P in terms of x and y .
Solution:

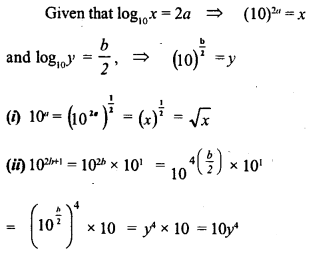
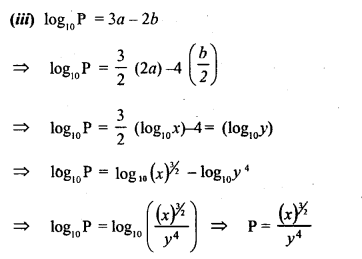
Question 10.
If log₂ y = x and log₃ z = x, find 72^x in terms of y and z.
Solution:

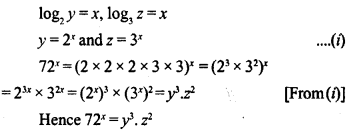
Question 11.
If log₂ x = a and log₅y = a, write 100^2a-1 in terms of x and y.
Solution:

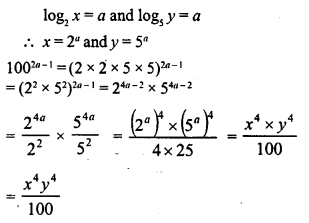
Exercise 9.2

Question 1.
Simplify the following :

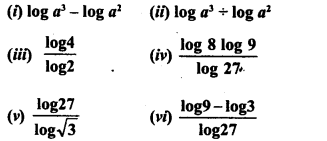
Solution:

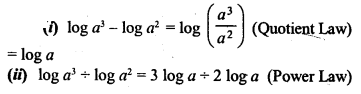
Question 2.
Evaluate the following:


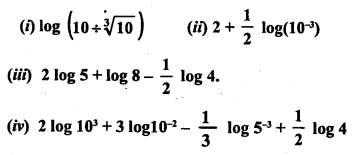
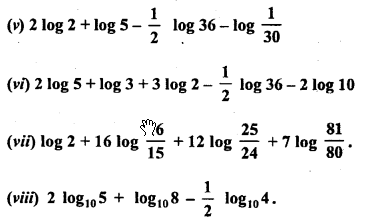
Solution:

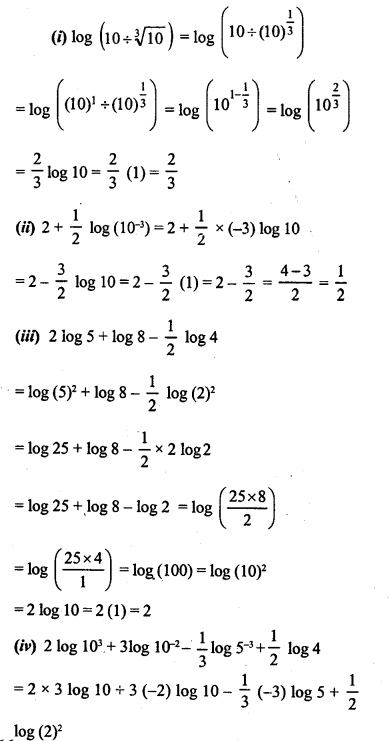
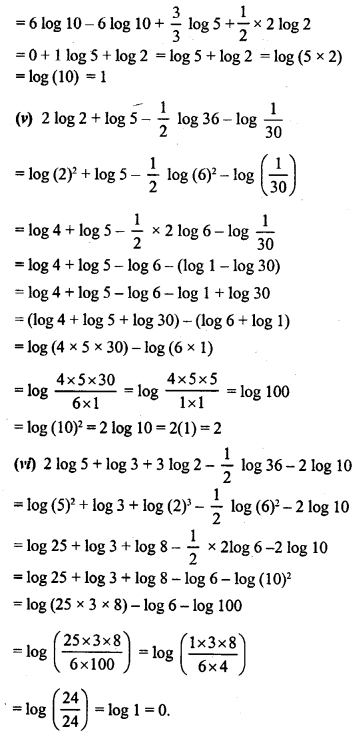
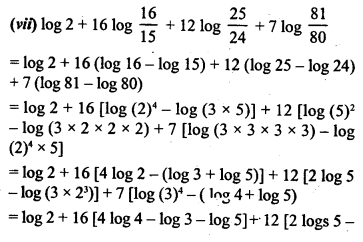
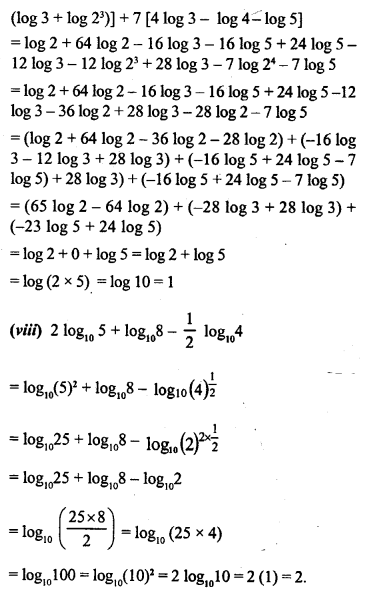
Question 3.
Express each of the following as a single logarithm:

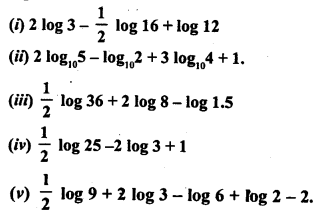
Solution:

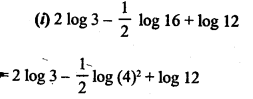
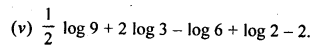
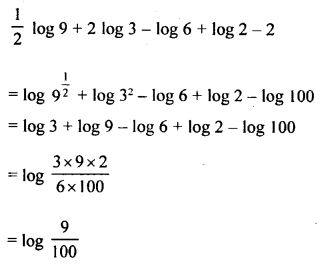
Question 4.
Prove the following :
(i) log₁₀ 4 ÷ log₁₀ 2 = l0g₃ 9
(ii) log₁₀ 25 + log₁₀ 4 = log₅ 25
Solution:

Question 5.
If x = 100)^a , y = (10000)^b and z = (10)^c, express

Solution:

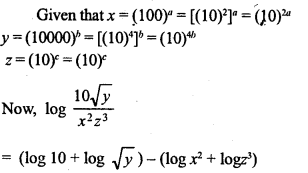
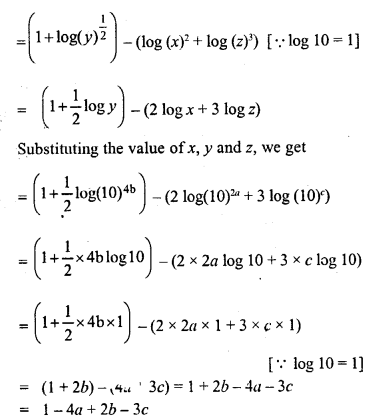
Question 6.
If a = log₁₀x, find the following in terms of a :
(i) x
(ii) log₁₀\(\sqrt [ 5 ]{ { x }^{ 2 } }\)
(iii) log₁₀5x
Solution:

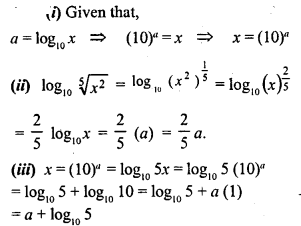
Question 7.

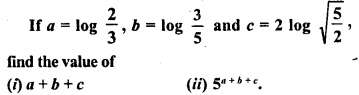
Solution:

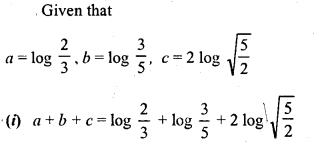
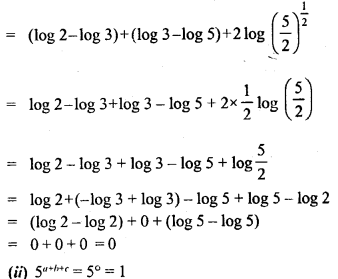
Question 8.

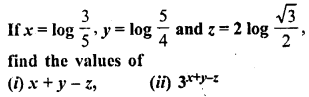
Solution:

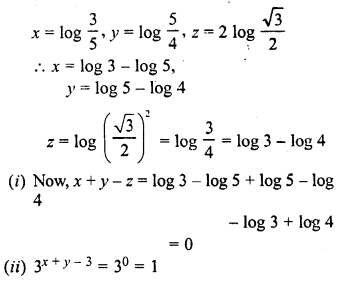
Question 9.
If x = log₁₀ 12, y = log₄ 2 x log₁₀ 9 and z = log₁₀ 0.4, find the values of
(i)x-y-z
(ii) 7^x-y-z
Solution:

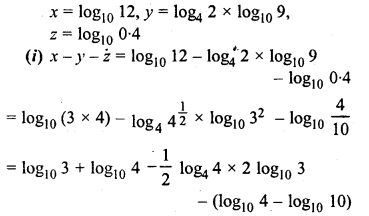
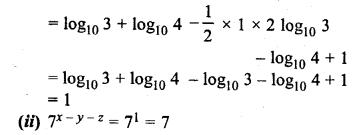
Question 10.
If log V + log3 = log π + log4 + 3 log r, find V in terns of other quantities.
Solution:

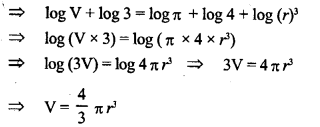
Question 11.
Given 3 (log 5 – log3) – (log 5-2 log 6) = 2 – log n , find n.
Solution:

Question 12.
Given that log₁₀y + 2 log₁₀x= 2, express y in terms of x.
Solution:

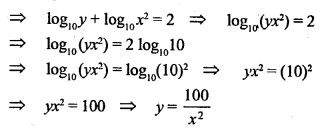
Question 13.
Express log₁₀2+1 in the from log₁₀x.
Solution:

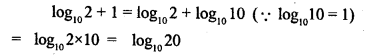
Question 14.

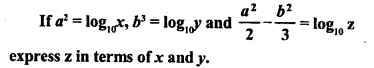
Solution:

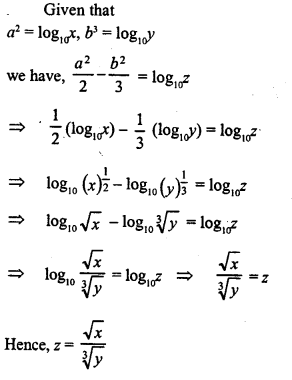
Question 15.
Given that log m = x + y and log n = x-y, express the value of log m²n in terms of x and y.
Solution:

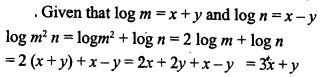
Question 16.

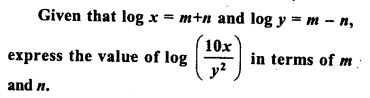
Solution:

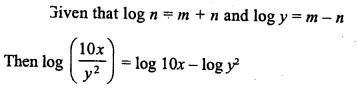
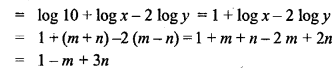
Question 17.

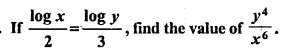
Solution:

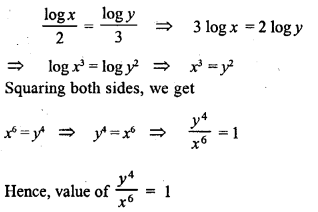
Question 18.
Solve for x:

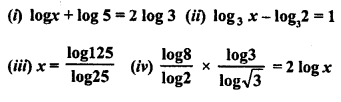
Solution:

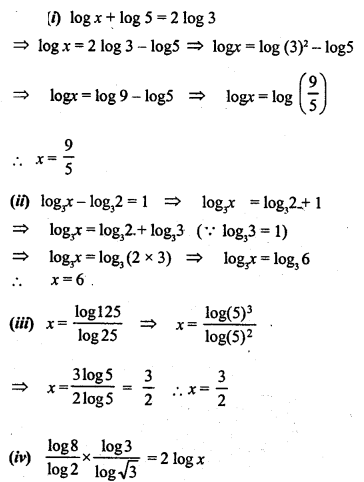
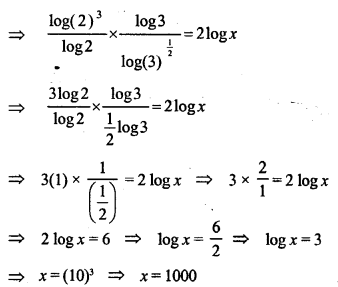
Question 19.
Given 2 log₁₀x+1= log₁₀250, find
(i) x
(ii) log₁₀2x
Solution:

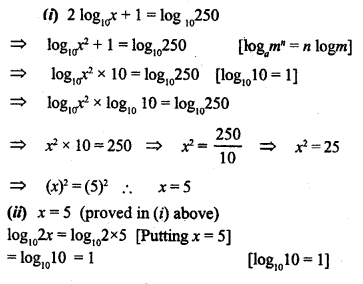
Question 20.

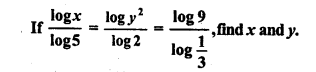
Solution:

Question 21.
Prove the following :
(i) 3^{_{log 4}} = 4^{_{log 3}}
(ii) 27^{_{log 2}} = 8^{_{log 3}}
Solution:

Question 22.
Solve the following equations :
(i) log (2x + 3) = log 7
(ii) log (x +1) + log (x – 1) = log 24
(iii) log (10x + 5) – log (x – 4) = 2
(iv) log₁₀5 + log₁₀(5x+1) = log₁₀(x + 5) + 1
(v) log (4y – 3) = log (2y + 1) – log3
(vi) log₁₀(x + 2) + log₁₀(x – 2) = log₁₀3 + 31og₁₀4.
(vii) log(3x + 2) + log(3x – 2) = 5 log 2.
Solution:

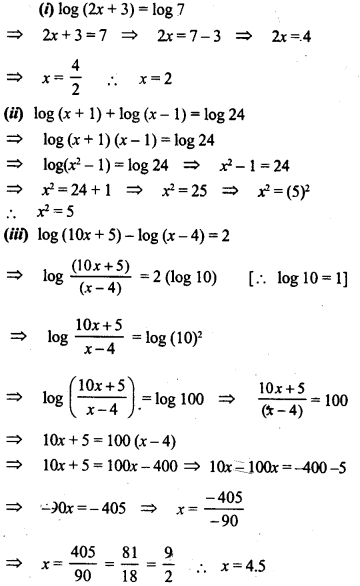
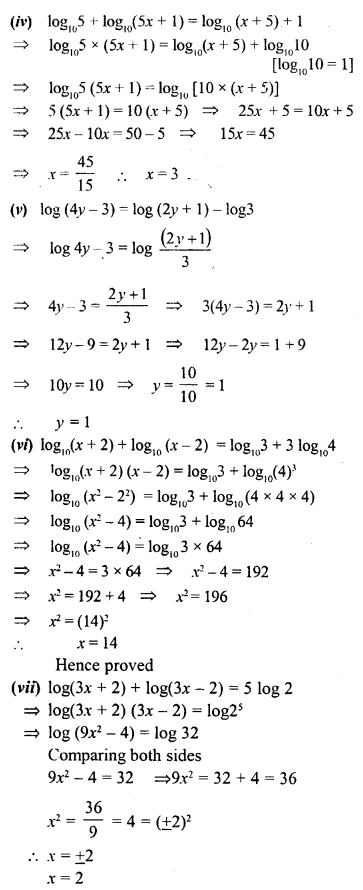
Question 23.
Solve for x :
log₃ (x + 1) – 1 = 3 + log₃ (x – 1)
Solution:

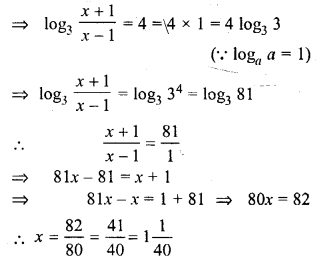
Question 24.

Solution:

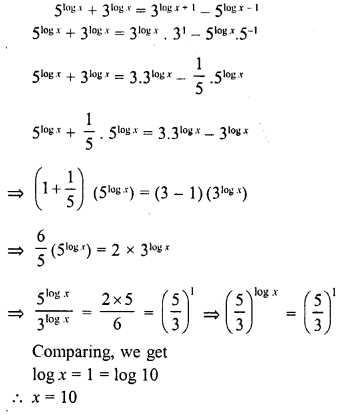
Question 25.

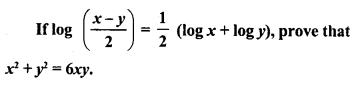
Solution:

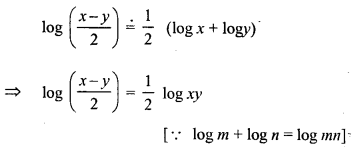
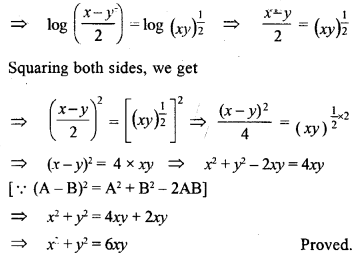
Question 26.

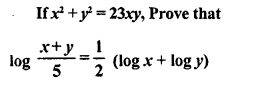
Solution:

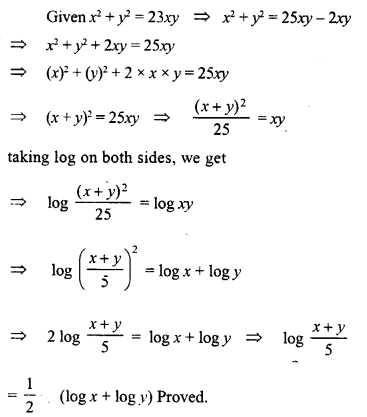
Question 27.
If p = log₁₀20 and q = log₁₀25, find the value of x if 2 log₁₀ (x +1) = 2p – q.
Solution:

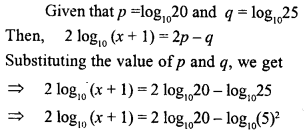
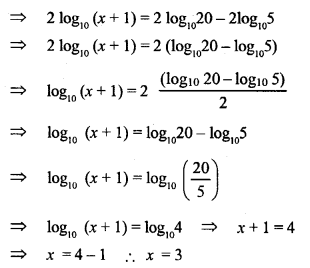
Question 28.
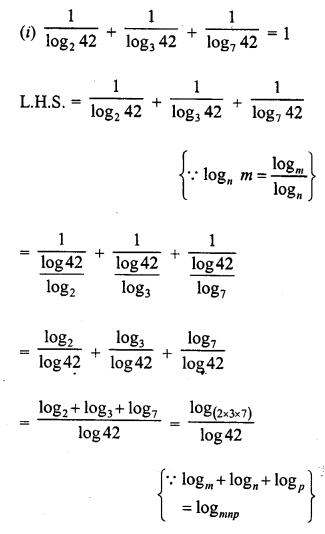
Show that:

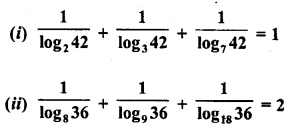
Solution:

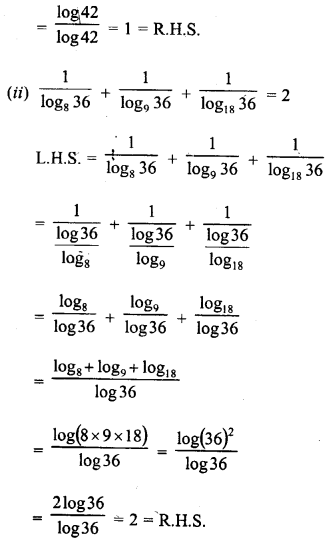
Question 29.
Prove the following identities:

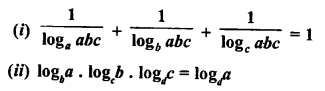
Solution:

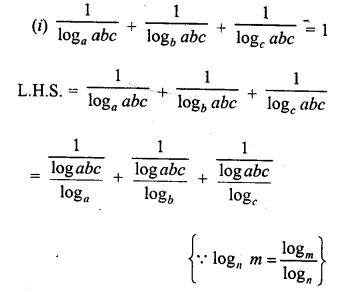
Question 30.

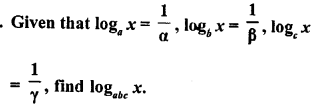
Solution:

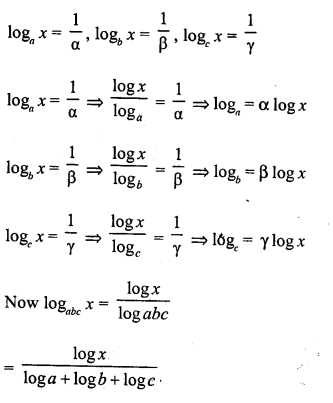
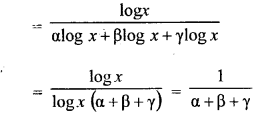
Question 31.
Solve for x :

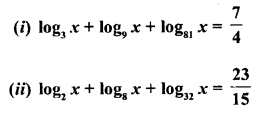
Solution:

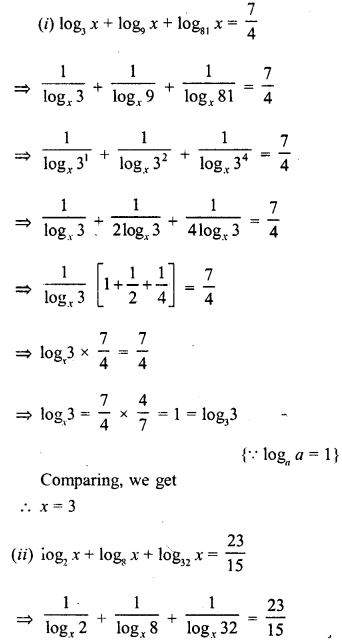
Multiple Choice Questions

correct Solution from the given four options (1 to 7):
Question 1.
If log√3 27 = x, then the value of x is
(a) 3
(b) 4
(c) 6
(d) 9
Solution:

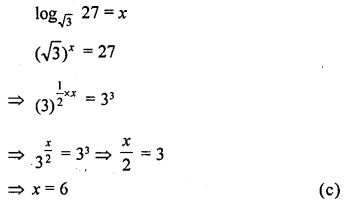
Question 2.
If log₅ (0.04) = x, then the vlaue of x is
(a) 2
(b) 4
(c) -4
(d) -2
Solution:

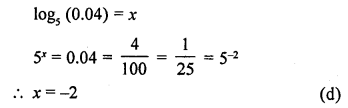
Question 3.
If log_0.5 64 = x, then the value of x is
(a) -4
(b) -6
(c) 4
(d) 6
Solution:

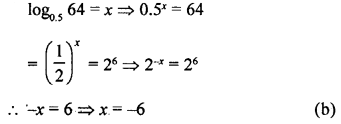
Question 4.
If log_{10\(\sqrt [ 3 ]{ 5 }\)} x = -3, then the value of x is

Solution:

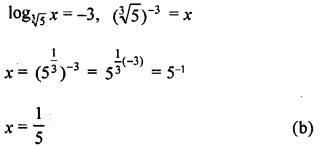
Question 5.
If log (3x + 1) = 2, then the value of x is

Solution:

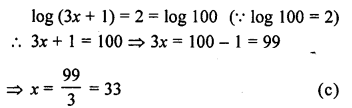
Question 6.
The value of 2 + log₁₀ (0.01) is
(a)4
(b)3
(c)1
(d)0
Solution:

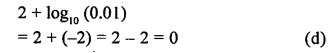
Question 7.


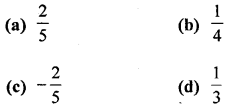
Solution:

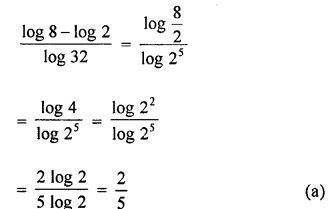
Chapter Test

Question 1.

Solution:

Question 2.
Find the value of log√3 3√3 – log₅ (0.04)
Solution:

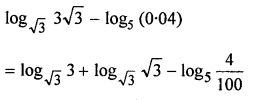
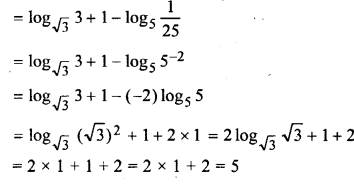
Question 3.
Prove the following:

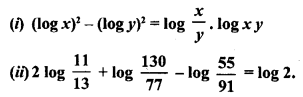
Solution:

Question 4.
If log (m + n) = log m + log n, show that n = \(\frac { m }{ m-1 }\)
Solution:

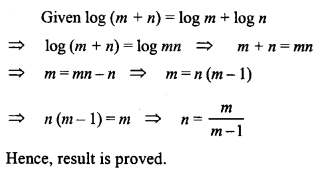
Question 5.

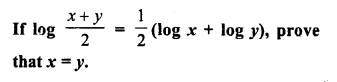
Solution:

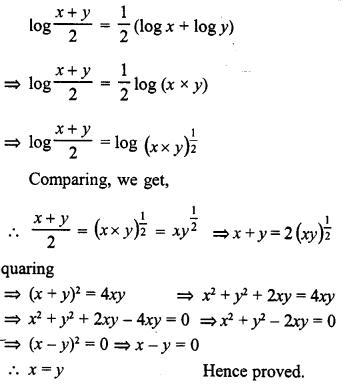
Question 6.

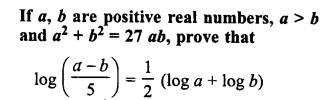
Solution:

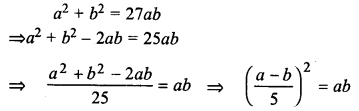
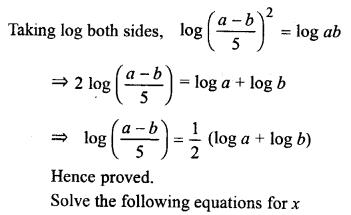
Question 7.
Solve the following equations for x:

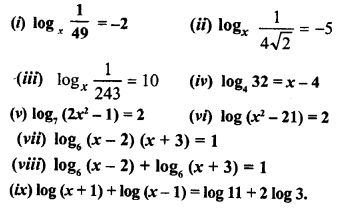
Solution:

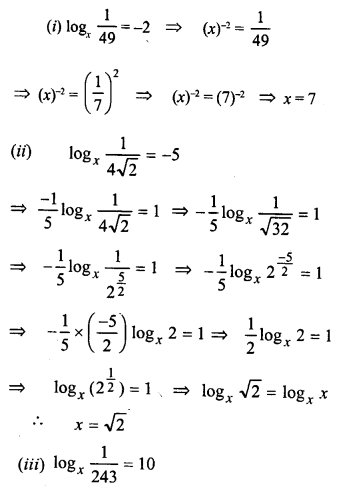
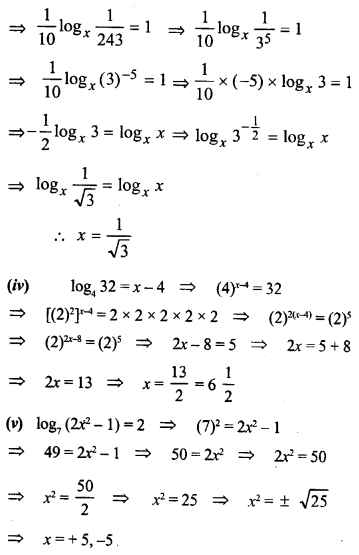
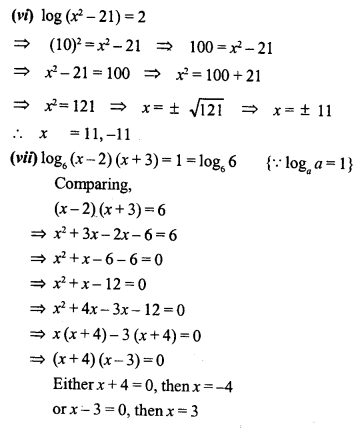
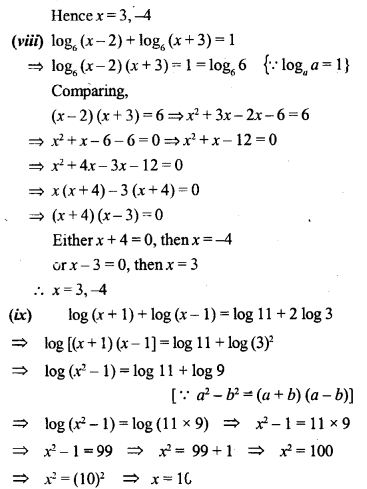
Question 8.
Solve for x and y:

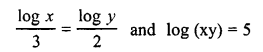
Solution:

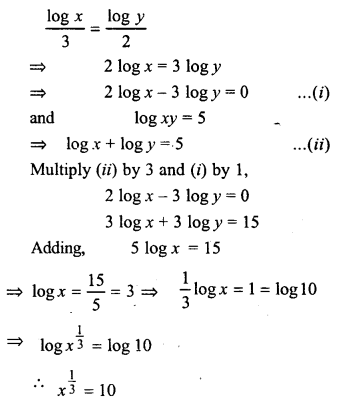
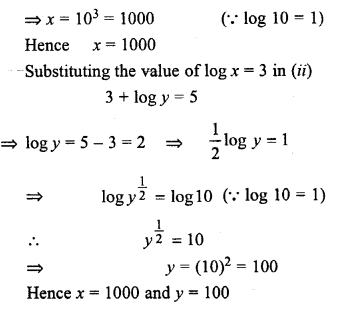
Question 9.
If a = 1 + log_xyz, 6 = 1+ log_y zx and c=1 + log_zxy, then show that ab + bc + ca = abc.
Solution: